什么是线段树?
线段树(Segment Tree)是一种基于分治思想的二叉树结构,用于在区间上进行信息统计。与树状数组相比,线段树是一种 更加通用的数据结构。
- 线段树每个节点都代表一个区间。
- 线段树具有唯一的根节点,代表的区间是整个统计范围,如 [1,N]。
- 线段树每个叶节点都代表一个长度为 1 的区间 [x,x]。
- 对于每个内部节点 [L,R],左子节点 [L,mid],右子节点 [mid+1,R],其中 mid=L+R>>1。
区间视角
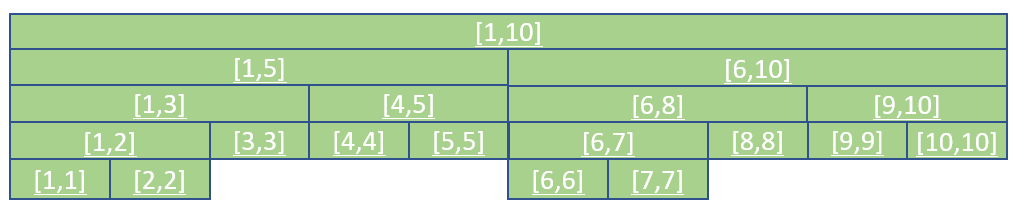
二叉树视角
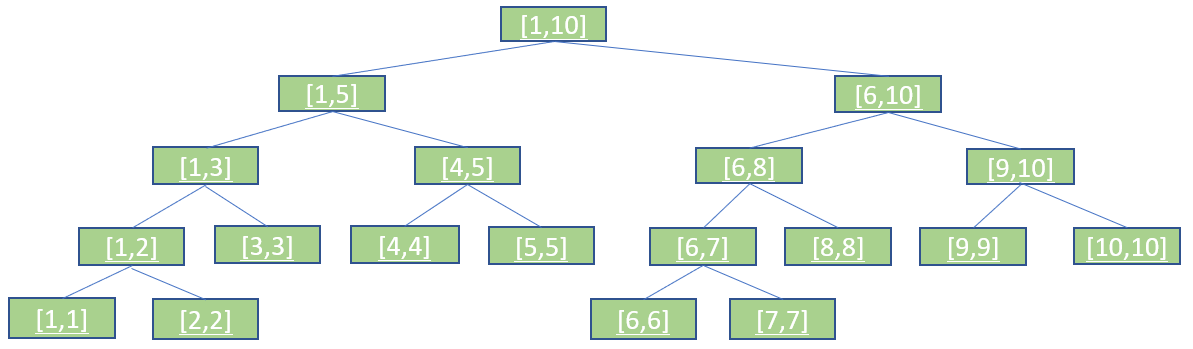
线段树数据结构设计
由于线段树是二叉树结构,最终要线性存储在内存当中,需要创建一块连续的空间用于存储线段树结构体。
如图所示:倒第二层数节点数量 ≤n,那么倒数第二层之前所有节点数量 ≤n-1,最后一层不论是否存满,都需要开 2n 空间。因此,至少要开 n + n - 1 + 2n = 4n - 1 空间,线段树数组 tr[4 * N]。
线段树结构体设计,至少包括区间 L, R,再根据实际情况确定其他信息,比如区间求最值,那么就再增加一个数据代表区间最值。这是树状数组无实现法的功能。
struct Node{
int L, R, dat; // dat 代表最大值
}tr[N * 4];
建树操作
给定一个长度是 N 的序列 A,在区间 [1,N] 上建立一颗线段树,每个叶节点 [i,i] 保存 A[i] 的值。线段树的二叉树结构很方便从上到下传递信息。以区间最大值为例,A={3,6,4,8,1,2,9,5,7,0},下标从 1 开始。
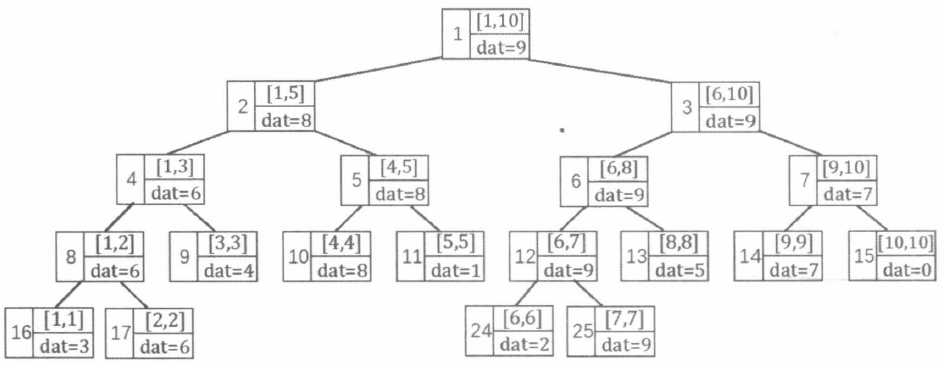
// 建树 调用 build(1, 1, N)
void build(int u, int L, int R){
tr[u] = {L, R};
// 返回条件 到叶子节点
if(L == R) return;
int mid = tr[u].L + tr[u].R >> 1;
// 分治建立左子树、右子树
build(u << 1, L, mid), build(u << 1 | 1, mid + 1, R);
}
建树调用 build(1, 1, n),u = 1 代表从根节点开始建树(即线段树节点编号),1 代表区间左边端点,n 代表 n 个数据,即区间右边端点。
单点更新
在线段树中,根节点即编号为 1 的节点是执行各种程序的入口。需要从根节点出发,递归找到代表区间 [x,x] 的叶节点,然后从下往上更新 [x,x] 以及其所有祖先节点上保存的信息,时间复杂度 O(logN)。
void pushup(int u){
tr[u].dat = max(tr[u << 1].dat, tr[u << 1 | 1].dat);
}
// 单点更新,将x位置数据更新为dat,调用build(1, 7, 1)
void update(int u, int x, int dat){
// 只有到叶子节点[x,x],才可以修改
if(tr[u].L == x && tr[u].R == x){
tr[u].dat = dat;
return;
}
int mid = tr[u].L + tr[u].R >> 1;
if(x <= mid) update(u << 1, x, dat);
else update(u << 1 | 1, x, dat);
pushup(u);
}
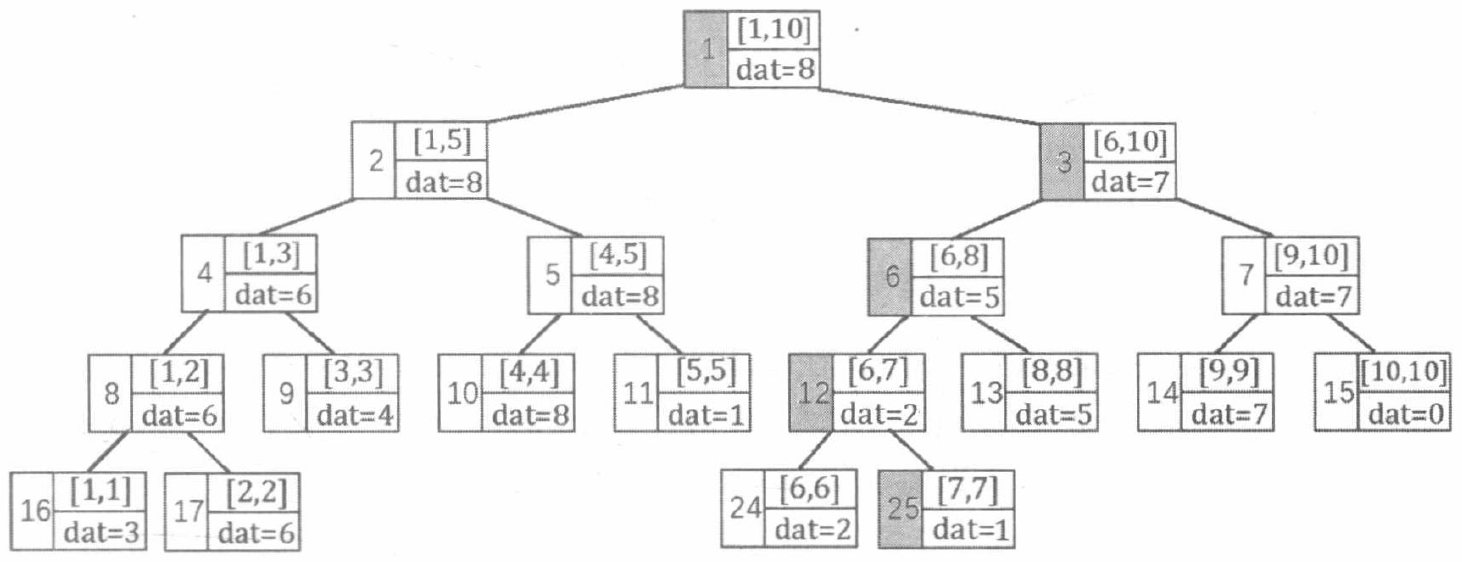
由于将线段树 [7,7] 区间里面的 dat 从之前的 9 更新为 1,而父节点是左右孩子区间数据的最大值,所以要执行 pushup 操作,向上将相应祖先节点数据进行更新。
区间查询
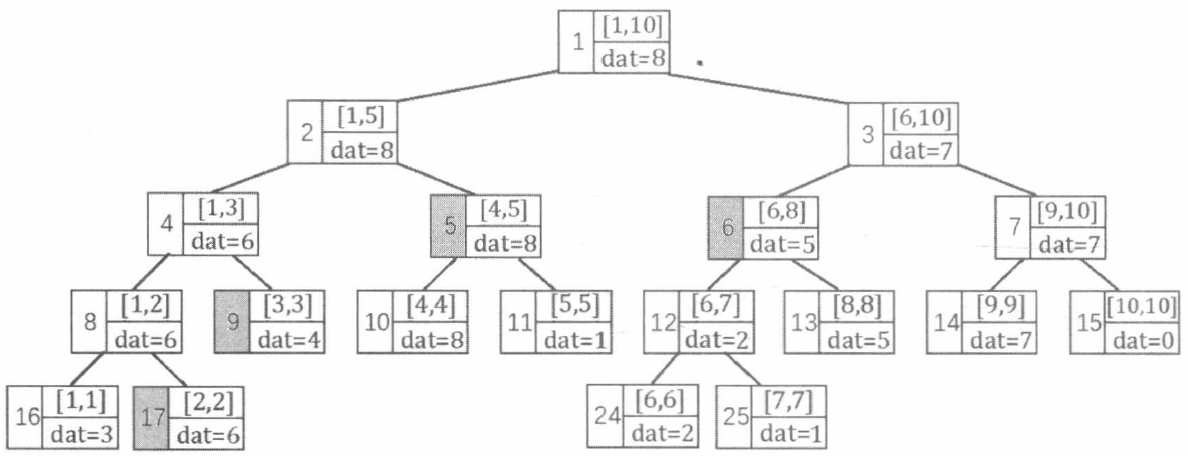
query(1, 2, 8) = max{6, 4, 8, 5} = 8
// 区间查询 调用 query(1, 2, 8)
int query(int u, int L, int R){
// 如果线段树节点左右区间完全包含在被询问区间[L, R]
if(tr[u].L >= L && tr[u].R <= R) return tr[u].dat;
int mid = tr[u].L + tr[u].R >> 1;
int res = 0;
if(L <= mid) res = query(u << 1, L, R);
if(R > mid) res = max(res, query(u << 1 | 1, L, R));
return res;
}
延迟标记
延迟标记用于区间修改,在之前的单点修改指令中,时间复杂度为 O(logN),但是区间修改最坏情况,即所有叶子节点都被修改,时间复杂度变成 O(N)。
然而,如果一次修改操作中,节点u所代表的区间 [tr[u].L,tr[u].R] 被 修改区间 [L,R] 完全覆盖,并且逐一更新了 u 子树中所有节点,之后的查询指令中却并没有用到 [L,R] 的子区间作为候选答案,那么更新节点 u 的整颗子树就是多余的操作。
因此,当我们在执行修改指令时,同样可以在 L≤tr[u].L≤tr[u].R≤R 的情况下立即返回,只不过在回溯之前向节点 u 增加一个标记 add,代表该节点曾经被修改,但其子节点尚未更新。
如果在后续的指令中,需要从节点 u 向下递归,再检查 u 是否具有 add 标记,如果有 add 标记,就根据标记信息更新 u 的两个子节点,同时为 u 的两个子节点增加 add 标记,最后清除 u 的 add 标记。
编程实战
黑猫OJ #B299. 最高分是多少
参考程序
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 3e4 + 10;
int n, m;
// 线段树结构体
struct Node{
int L, R, dat; // dat 代表[L, R]之间的最大值
}tr[N * 4];
void pushup(int u){
tr[u].dat = max(tr[u << 1].dat, tr[u << 1 | 1].dat);
}
// 建树
void build(int u, int L, int R){
tr[u] = {L, R};
// 判断是否为叶子节点
if(tr[u].L == tr[u].R) return;
int mid = tr[u].L + tr[u].R >> 1;
build(u << 1, L, mid), build(u << 1 | 1, mid + 1 , R);
}
// 更新操作 将x位置的数更改为dat
void update(int u, int x, int dat){
// 找叶子节点
if(tr[u].L == x && tr[u].R == x){
tr[u].dat = dat;
return;
}
int mid = tr[u].L + tr[u].R >> 1;
if(x <= mid) update(u << 1, x, dat);
else update(u << 1 | 1, x, dat);
pushup(u);
}
int query(int u, int L, int R){
if(tr[u].L >= L && tr[u].R <= R) return tr[u].dat;
int mid = tr[u].L + tr[u].R >> 1;
int res = 0;
if(L <= mid) res = query(u << 1, L, R);
if(R > mid) res = max(res, query(u << 1 | 1, L, R));
return res;
}
int main() {
while(~scanf("%d%d", &n, &m)){
build(1, 1, n);
for(int i = 1; i <= n; i++){
int t;
scanf("%d", &t);
update(1, i, t);
}
while(m--){
char op[2];
int a, b;
scanf("%s%d%d", op, &a, &b);
if(*op == 'U') update(1, a, b);
else printf("%d\n", query(1, a, b));
}
}
return 0;
}
黑猫OJ #B300. 区间查询
参考程序
#include <iostream>
#include <cstdio>
#include <string>
using namespace std;
const int N = 3e4 + 10;
struct Node{
int L, R, dat; // dat代表[L, R]之间所有数据之和
}tr[N * 4];
void pushup(int u){
tr[u].dat = tr[u << 1].dat + tr[u << 1 | 1].dat;
}
void build(int u, int L, int R){
tr[u] = {L, R};
// 判断是否为叶子节点
if(tr[u].L == tr[u].R) return;
int mid = tr[u].L + tr[u].R >> 1;
build(u << 1, L, mid), build(u << 1 | 1, mid + 1 , R);
}
void update(int u, int x, int dat){
if(tr[u].L == x && tr[u].R == x){
tr[u].dat += dat;
return;
}
int mid = tr[u].L + tr[u].R >> 1;
if(x <= mid) update(u << 1, x, dat);
else update(u << 1 | 1, x, dat);
pushup(u);
}
int query(int u, int L, int R){
if(tr[u].L >= L && tr[u].R <= R) return tr[u].dat;
int mid = tr[u].L + tr[u].R >> 1;
int res = 0;
if(L <= mid) res = query(u << 1, L, R);
if(R > mid) res += query(u << 1 | 1, L, R);
return res;
}
int main() {
int T, cnt = 0;
cin >> T;
while(T--){
int n;
scanf("%d", &n);
build(1, 1, n);
for(int i = 1; i <= n; i++){
int t;
scanf("%d", &t);
update(1, i, t);
}
string op;
printf("Case %d:\n", ++cnt);
while(cin >> op, op != "End"){
int a, b;
scanf("%d%d", &a, &b);
if(op == "Add") update(1, a, b);
else if(op == "Sub") update(1, a, -1*b);
else printf("%d\n", query(1, a, b));
}
}
return 0;
}
黑猫OJ #B303. 一个简单的整数问题
参考程序
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
int n, m;
int a[N];
struct Node{
int L, R;
LL sum, add;
}tr[N * 4];
void pushup(int u){
tr[u].sum = (LL)(tr[u << 1].sum + tr[u << 1 | 1].sum);
}
void pushdown(int u){
auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
if(root.add){
left.add += root.add, left.sum += (LL)(left.R - left.L + 1) * root.add;
right.add += root.add, right.sum += (LL)(right.R - right.L + 1) * root.add;
root.add = 0;
}
}
void build(int u, int L, int R){
if(L == R){
tr[u] = {L, R, a[L], 0};
return;
}
tr[u] = {L, R};
int mid = tr[u].L + tr[u].R >> 1;
build(u << 1, L, mid), build(u << 1 | 1, mid + 1, R);
pushup(u);
}
void update(int u, int L, int R, int d){
if(tr[u].L >= L && tr[u].R <= R){
tr[u].sum += (LL)(tr[u].R - tr[u].L + 1) * d;
tr[u].add += d;
return;
}
pushdown(u);
int mid = tr[u].L + tr[u].R >> 1;
if(L <= mid) update(u << 1, L, R, d);
if(R > mid) update(u << 1 | 1, L, R, d);
pushup(u);
}
LL query(int u, int L, int R){
if(tr[u].L >= L && tr[u].R <= R) return tr[u].sum;
pushdown(u);
int mid = tr[u].L + tr[u].R >> 1;
LL res = 0;
if(L <= mid) res = query(u << 1, L, R);
if(R > mid) res += query(u << 1 | 1, L, R);
return res;
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
build(1, 1, n);
while(m--){
char op[2];
int L, R, d;
scanf("%s%d%d", op, &L, &R);
if(*op == 'C'){
scanf("%d", &d);
update(1, L, R, d);
}
else printf("%lld\n", query(1, L, R));
}
return 0;
}