什么是排序算法?
排序算法是一种用于将一组元素按照一定顺序排列的算法。这种排序可以按照升序(从小到大)或降序(从大到小)的方式进行。排序算法是计算机科学中的基本问题之一,因为在实际应用中,经常需要对数据进行排序以便更方便地进行搜索、查找或其他操作。
之前,我们学习过 sort 排序库函数,本节我们讲解几种常见排序算法原理。
排序算法稳定性
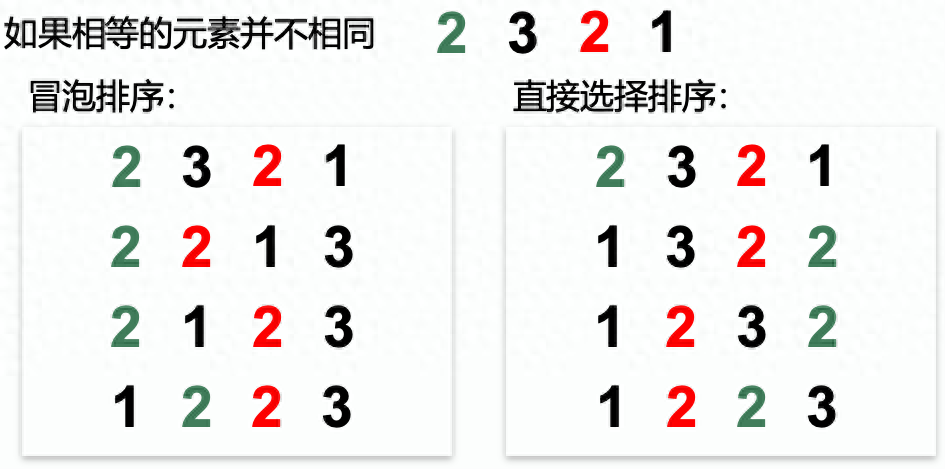
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,则称这种排序算法是稳定的;否则称为不稳定的。
稳定的排序可以利用上一次的排序结果,来服务这次的排序。
判断方法:排序时是否只有相邻元素交换。如果是,那么排序算法稳定的;如果不是,那么排序算法是不稳定的。
稳定排序库函数
sort 是不稳定排序,平均时间复杂度为 O(nlogn)。
stable_sort 是稳定排序,平均时间复杂度也为 O(nlogn)。
stable_sort(起始元素指针,最后一个元素的指针的后一个位置, 比较函数);
//对数组 a下标 1 到 n 进行排序
stable_sort(a+1,a+1+n, cmp);
比较函数:传入两个数组中元素类型的参数,返回第一个参数排在前面的条件。
若不写比较函数cmp,默认为升序排序。

选择排序
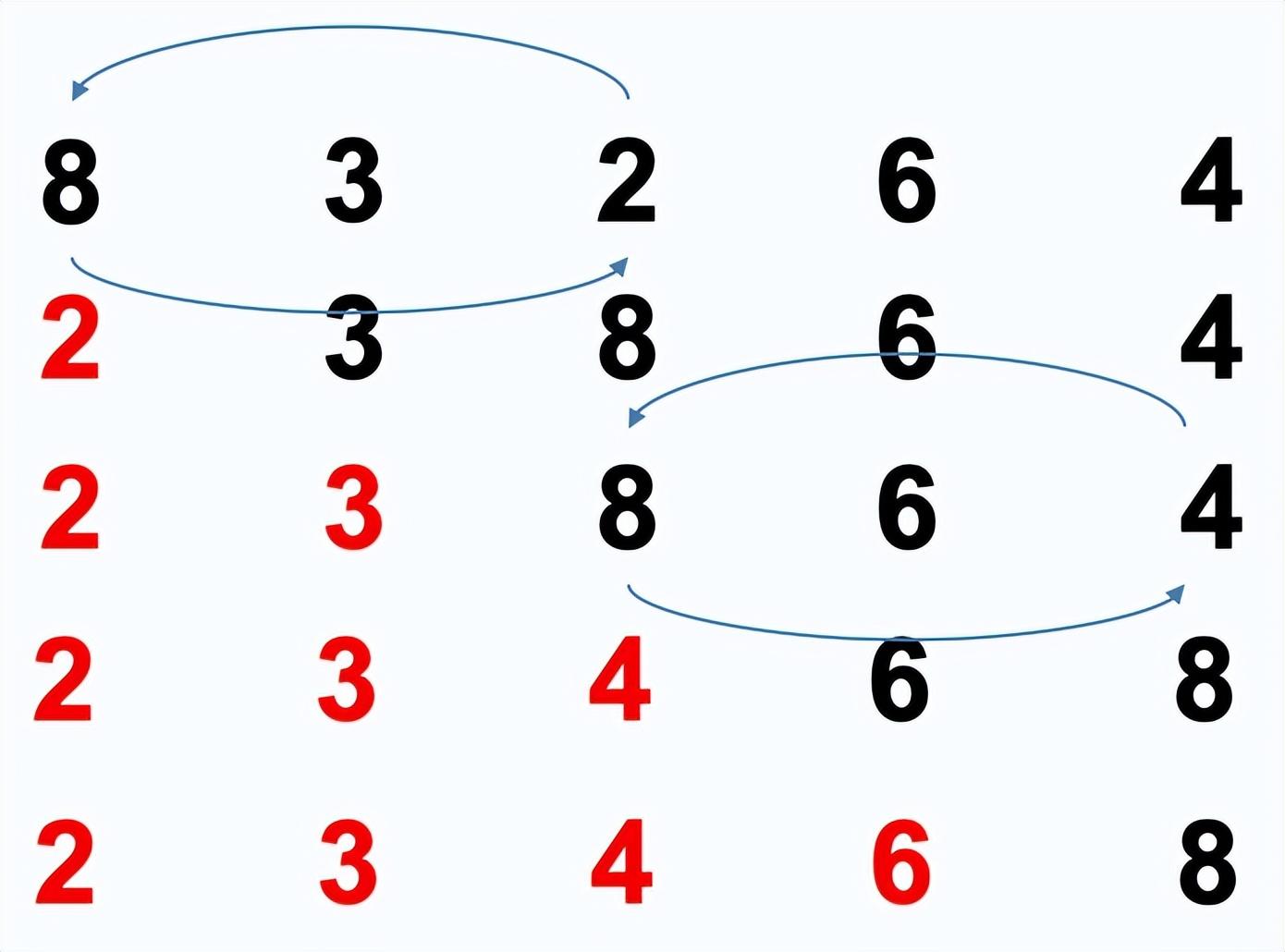
选择排序:每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在待排序的数列的最前面。
时间复杂度:, 辅助空间复杂度:, 不稳定。
#include <iostream>
using namespace std;
int n;
int a[110];
int main(){
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
// n - 1 轮循环
for(int i = 1; i < n; i++){
int idx = -1, minv = 1e9;
for(int j = i + 1; j <= n; j++){
if(a[j] < a[i] && a[j] < minv){
minv = a[j];
idx = j;
}
}
if(idx != -1)
swap(a[i], a[idx]);
}
for(int i = 1; i <= n; i++) cout << a[i] << " ";
return 0;
}
冒泡排序
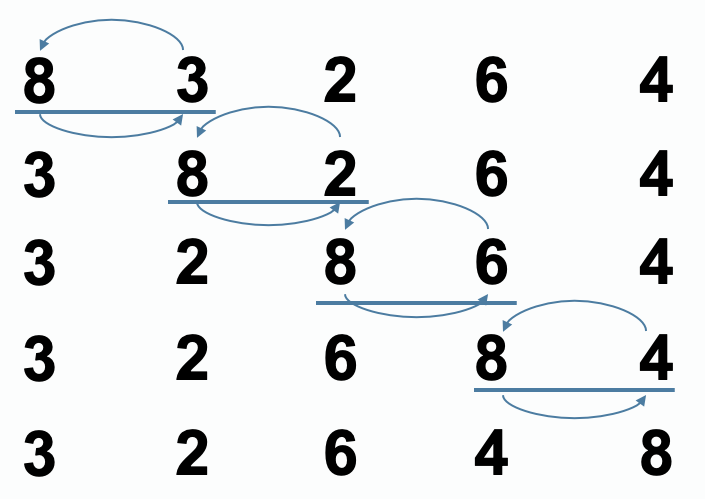
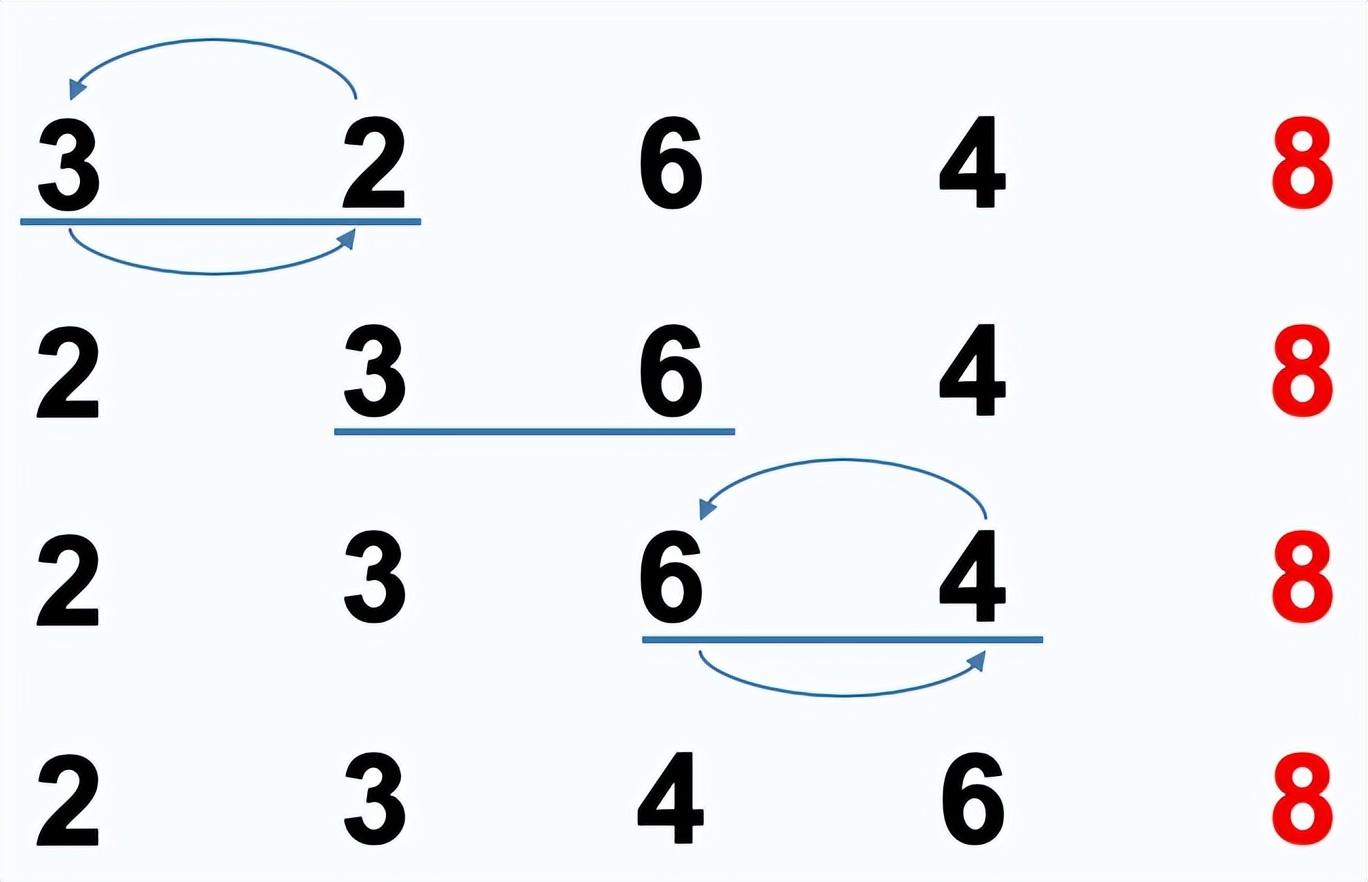
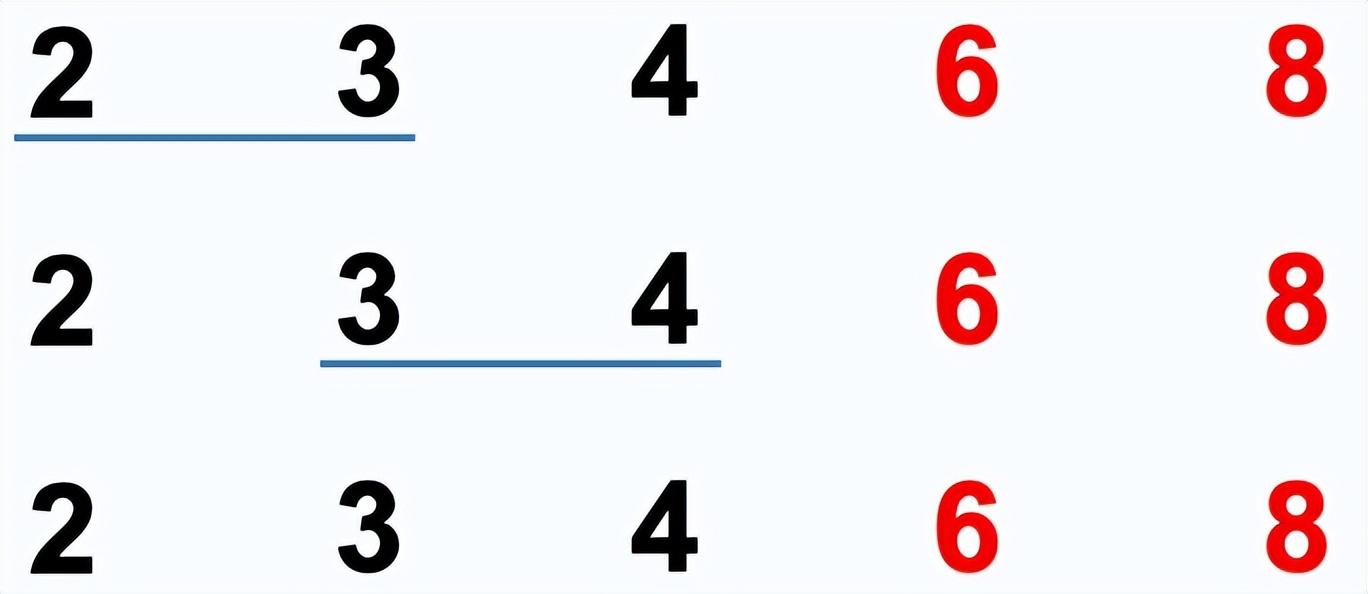
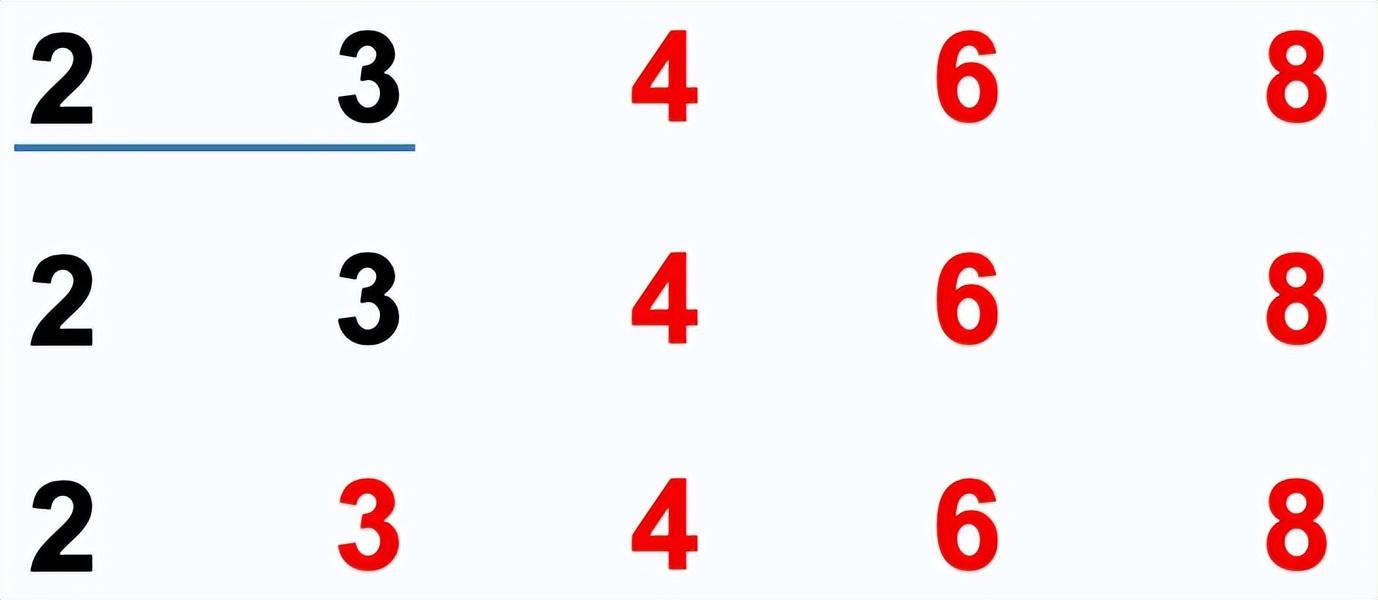
冒泡排序:依次比较两个相邻的元素,如果顺序错误就把他们交换过来。每次冒泡,最大(最小)的元素会经由交换“浮”到序列顶端。多次冒泡后,即可完成排序。
时间复杂度:, 辅助空间复杂度:,稳定。
冒泡排序——朴素版
#include <iostream>
using namespace std;
int n;
int a[110];
int main(){
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i < n; i++){
for(int j = 1; j <= n - i; j++){
if(a[j] > a[j + 1])
swap(a[j], a[j + 1]);
}
}
for(int i = 1; i <= n; i++) cout << a[i] << " ";
return 0;
}
冒泡排序优化——提前跳出:如果序列已经有序,就没有必要进行后面的循环。
#include <iostream>
using namespace std;
int n;
int a[110];
int main(){
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i < n; i++){
bool flag = true;
for(int j = 1; j <= n - i; j++){
if(a[j] > a[j + 1]){
swap(a[j], a[j + 1]);
flag = false;
}
}
if(flag) break;
}
for(int i = 1; i <= n; i++) cout << a[i] << " ";
return 0;
}
插入排序

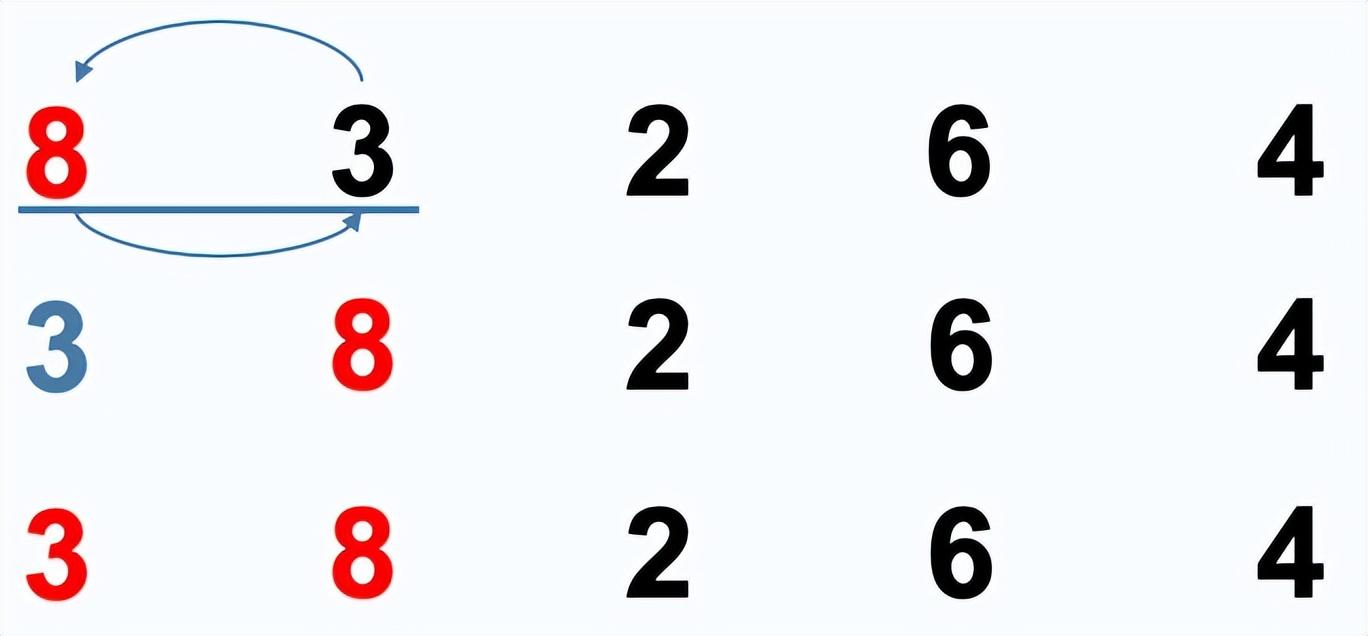
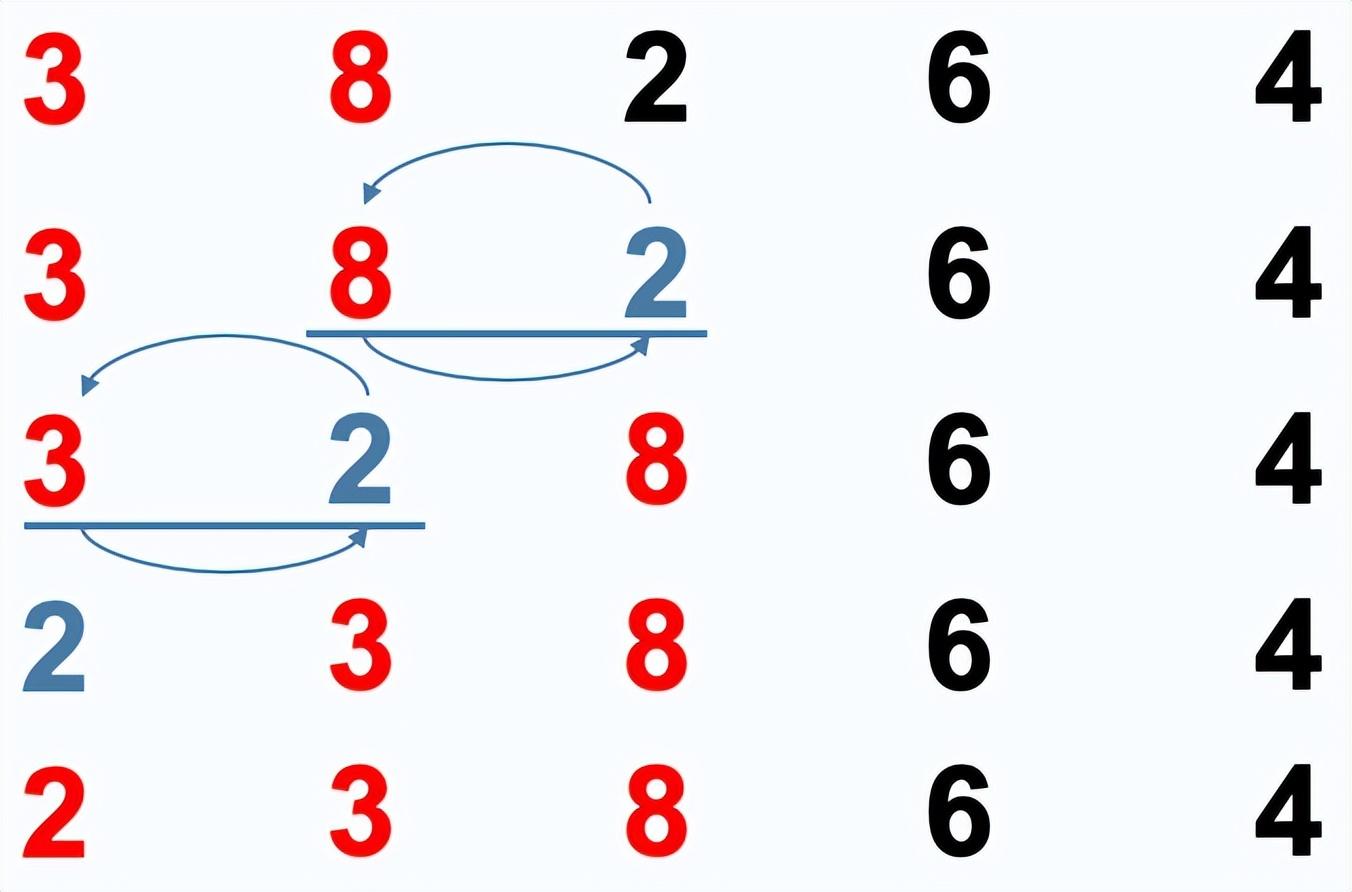
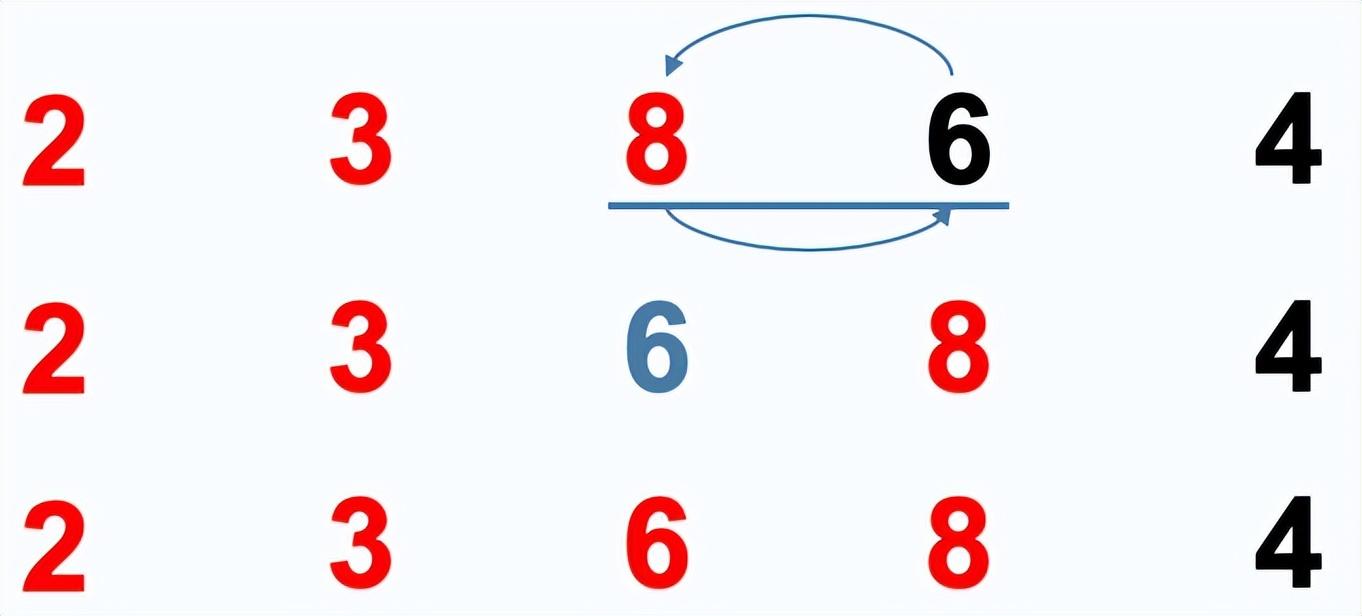
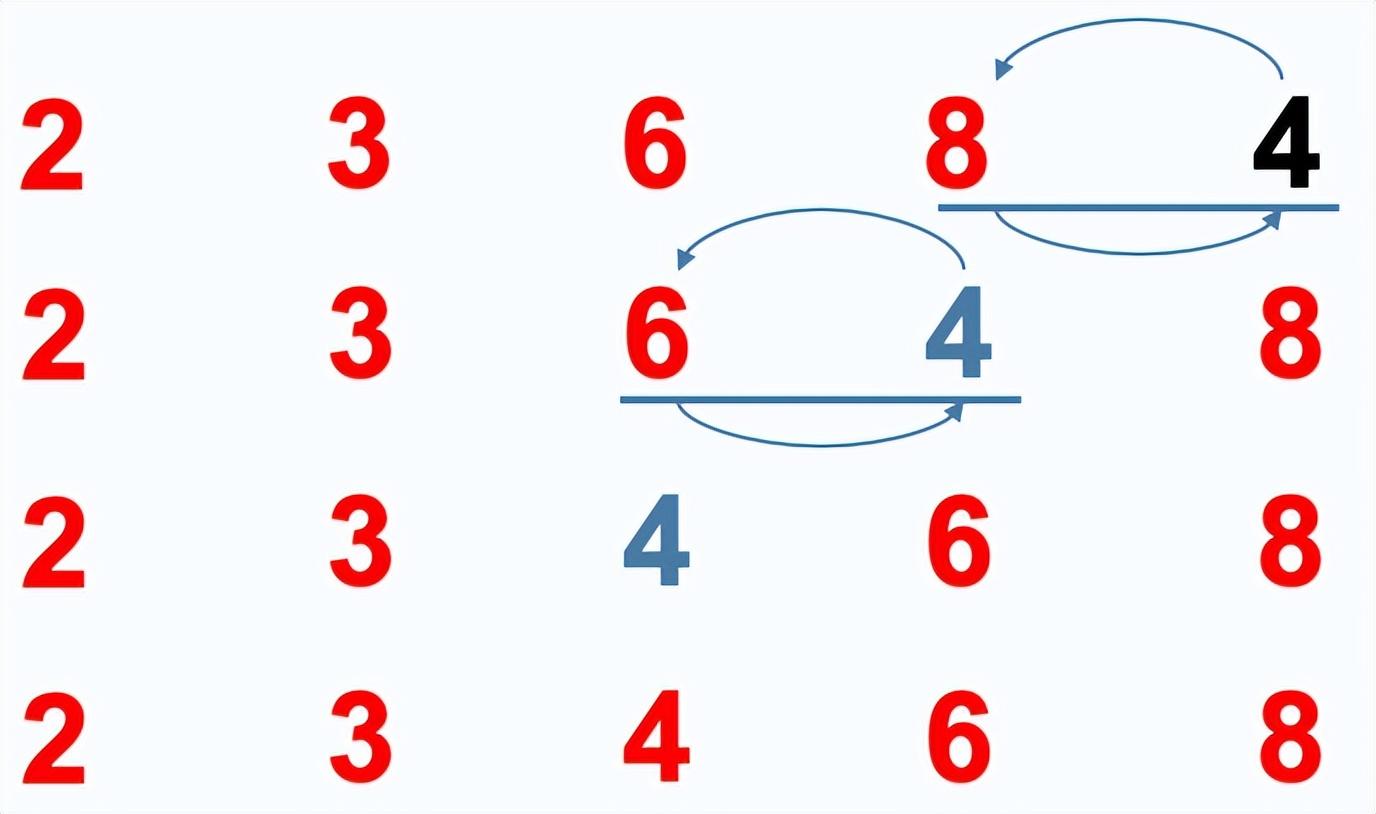
插入排序:假设前面n-1个数已经是有序的,现将第n个数插到前面已经有序的序列中,使得插入后这个序列仍然是有序的。
时间复杂度:, 辅助空间复杂度:,稳定。
方案1:
#include <iostream>
using namespace std;
int n;
int a[110];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
// 插入排序
for (int i = 2; i <= n; i++) {
int t = a[i];
int k = 1;
while (a[k] <= t && k < i) k++;
for (int j = i; j > k; j--) a[j] = a[j - 1];
a[k] = t;
}
for (int i = 1; i <= n; i++) cout << a[i] << " ";
return 0;
}
方案2:
#include <iostream>
using namespace std;
int n;
int a[110];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
// 插入排序
for (int i = 2; i <= n; i++) {
int j = i;
while(j && a[j] < a[j - 1]){
swap(a[j], a[j - 1]);
j--;
}
}
for (int i = 1; i <= n; i++) cout << a[i] << " ";
return 0;
}
桶排序
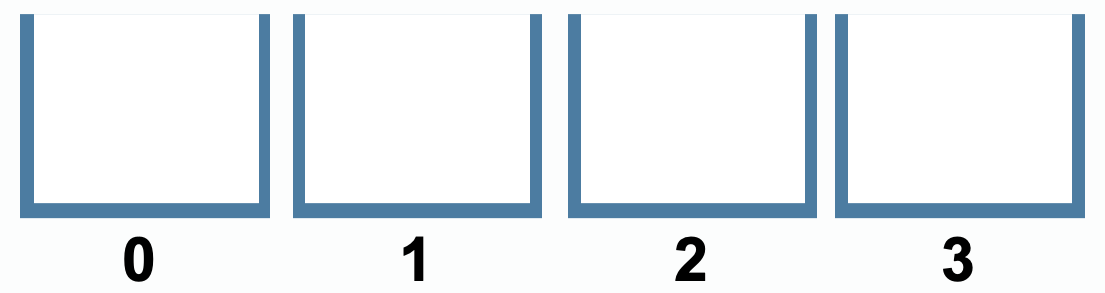
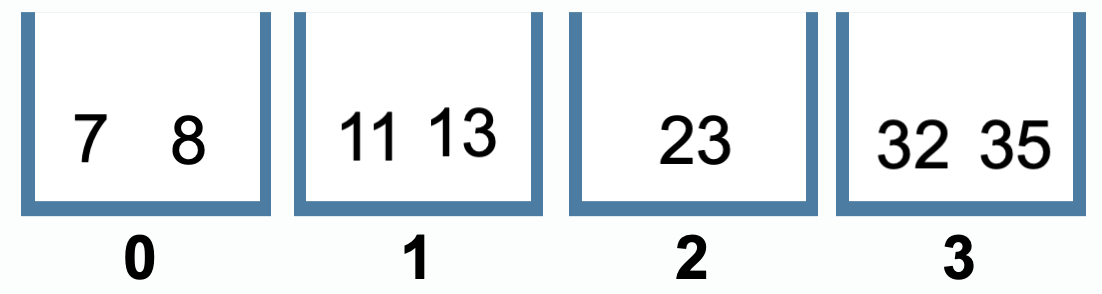
桶排序:将数据分到有限数量的有序的桶里,每个桶内分别排序,最后将各个桶中的数据合并。
数据分配到桶:散列过程

计数排序
计数排序:是一种特殊的桶排序。桶的个数是可能出现的数据种类数。
计数数组:数组下标是桶的编号,通常为数据值,
数组的值表示数据个数。
适用条件:待排序数据为整数,数据范围有限。
设数据个数为n,数据范围为k。
时间复杂度:O(n+k),额外空间复杂度:O(k),稳定。
构造计数数组
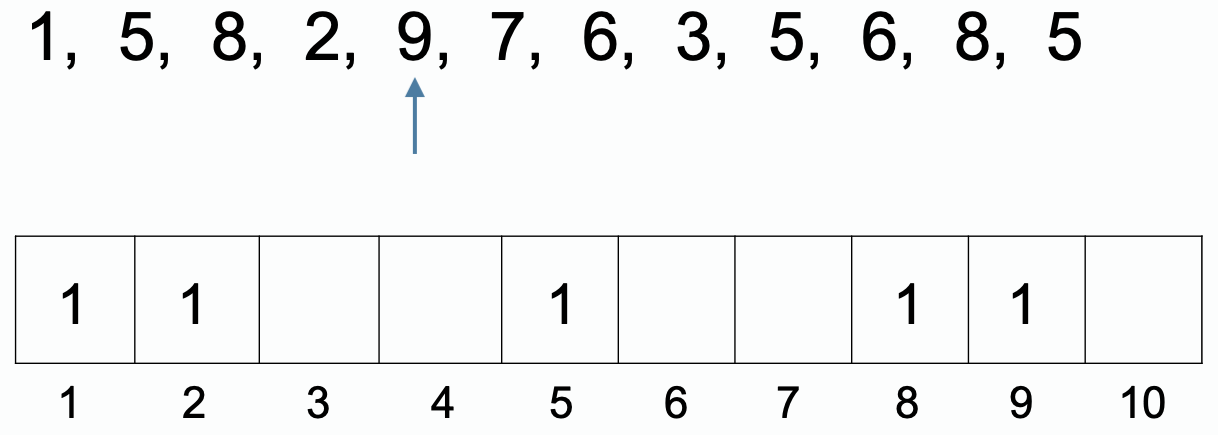
最终数组:

至此,排序已经完成,但是并不稳定。
构造前缀和 cnts 数组:

结果数组为 results:results[--cnts[a[i]]] = a[i];
res:1 2 3 5 5 5 6 6 7 8 8 9
idx:0 1 2 3 4 5 6 7 8 910 11
#include <iostream>
using namespace std;
const int N = 1010;
int n;
int a[N], cnts[N], results[N];
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
cnts[a[i]]++;
}
for (int i = 1; i < N; i++)
cnts[i] += cnts[i - 1];
// 为了稳定排序,从后向前遍历
for (int i = n - 1; i >= 0; i--)
results[--cnts[a[i]]] = a[i];
for (int i = 0; i < n; i++)
cout << results[i] << " ";
return 0;
}