什么是递推算法？

递推算法，是指从已知的初始条件出发，依据某种递推关系，逐次推出所要求的各中间结果及最后结果。

特点：

1.问题可以划分成多个状态；

2.除初始状态外，其它各个状态都可以用固定的递推关系式来表示。

首要问题：得到相邻的数据项间的关系（即递推关系）。

一般来说，可以将递推算法看成是一种特殊的迭代算法。

递推与迭代比较，两者的时间复杂度是相同的。所不同的是，递推往往设置数组，而迭代只要设置迭代的简单变量即可。

递推过程中数组变量带有下标，推出过程比迭代更为清晰。也正因为递推中应用数组，因此保留了递推过程中的中间数据。

递推关系式

给定一个数的序列 $F_0,F_1,...,F_n$，若存在整数 $n_0$，使当 $n>n_0$ 时，可以用符号（或大于号、小于号）将 $F_n$ 与其前面的某些项$F_i(0<i<n)$ 联系起来，这样的式子就叫做递推关系式。例如：$F_n=F_{n-1}+F_{n-2}$

解决递推问题的一般步骤：

1.建立递推关系式（顺推或逆推）；

2.确定边界条件（即初始值）；

3.递推求解。

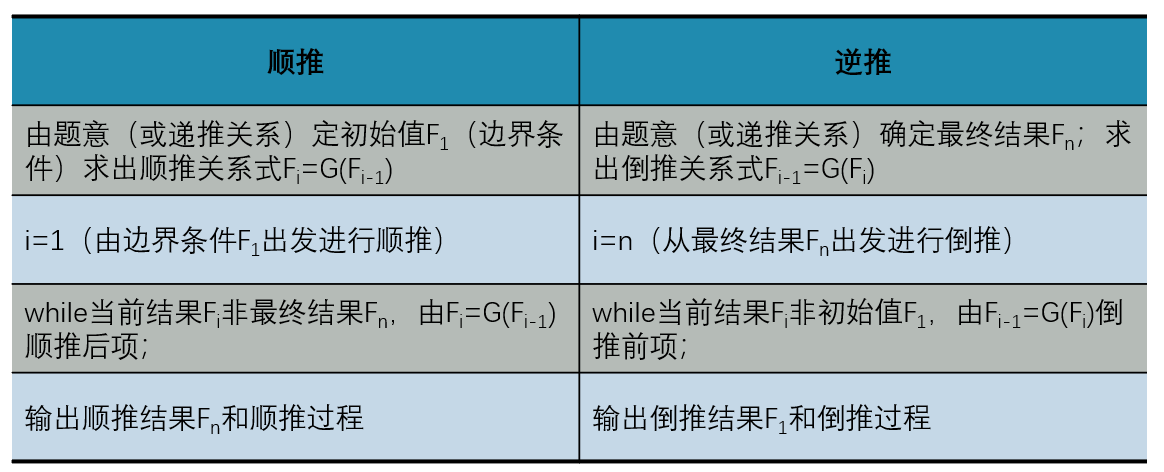
例题：骨牌铺法1

题目描述

有1*n的一个长方形，用一个1*1、1*2、1*3的骨牌铺满方格。例如n=3时为1*3的方格。此时用1*1、1*2、1*3的骨牌铺满方格，共有四种铺法。即3个1*1、1个1*1+1个1*2、1个1*2+1个1*1、1个1*3。

输入格式

一个整数n，代表方格的长度。

输出格式

铺法总数。（n≤50）

样例

3

4

解析：铺到第 n 个方格时，可以从 n-1 个方格再铺一个，可以从 n-2 个方格再铺一个，也可以从 n-3 个方格再铺一个。

递推公式：$F_n=F_{n-1}+F_{n-2}+F_{n-3}$

例题：骨牌铺法2

题目描述

有2×n的一个长方形方格，用一个1×2的骨牌铺满方格。例如n=3时，为2×3方格。此时用一个1×2的骨牌铺满方格，共有3种铺法：

输入格式

一行，一个整数n。（1≤n≤50）

输出格式

一行，一个整数，代表铺法总数。

样例

3

3

解析：

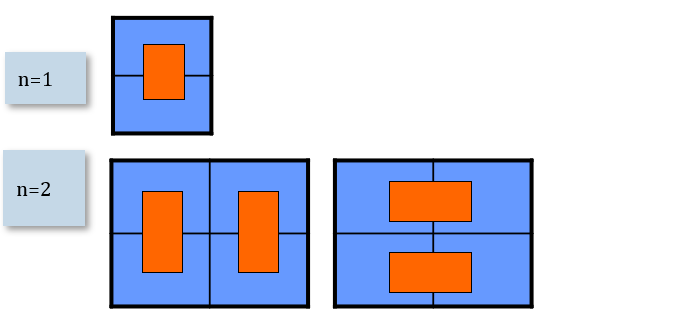
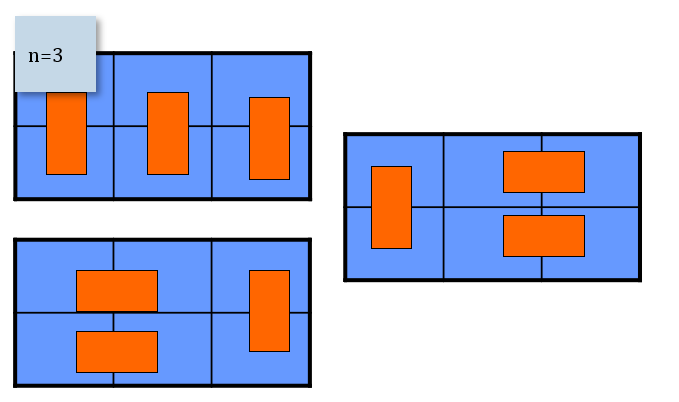
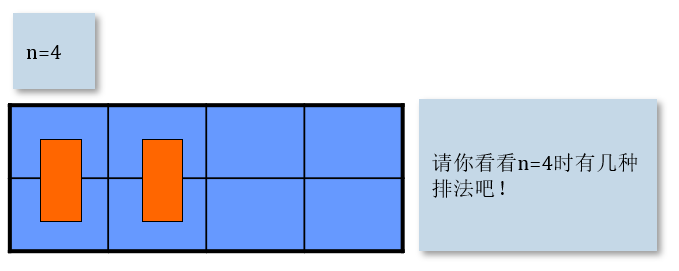
递推公式：$F_n=F_{n-1}+F_{n-2}$

五种典型递推关系

• Fibonacci 数列-兔子繁殖问题：$F_n=F_{n-1}+F_{n-2}$

• Hanoi 塔移动次数问题：$F_n=2F_{n-1}+1$

• 平面分割问题：设有n条封闭曲线画在平面上，而任何两条封闭曲线恰好相交于两点，且任何三条封闭曲线不相交于同一点，问这些封闭曲线把平面分割成的区域个数。

  • 每当增加一个椭圆时，由于与之前的每个圆都相交于不同的两点，而两点间的圆弧就能构成新的区域，则每增加一个椭圆，原区域都被分割成两份。
  • 递推公式：$F_n=F_{n-1}+2(n-1)$

  

第二类 Stirling 数

题目描述

n个有区别的球放到m个相同的盒子中，要求无一空盒，其不同的方案用F(n,m)表示，称为第二类Stirling数。

输入格式

两个正整数n和m，1≤n,m≤20。

输出格式

输出结果。

样例

4 2

7

解析：

• 重点：盒子不能为空，当已经有n-1个球放入盒子中时。第n个球放入时只能有两种情况：
  • 第n球独占一盒子时，前面n-1球只能放在m-1个盒子中，方案数为F(n-1,m-1)
  • 第n球与其他球共占同一盒子时，其他n-1球放入m个盒子中，有F(n-1,m)种，而n可放入m个盒中的任意一种，即有mF(n-1,m)种
• 递推公式：$F_n=F_{n-1,m-1}+mF_{n-1,m}$

凸多边形三角形划分

解析：凸 n 边形的任意一条边都必然是一个三角形的一条边，因为不在同一直线上的三点确定一个三角形，可以在 p[2]、p[3]、……、p[n-1]中找出一点与 p[1]、p[n] 构成一个三角形，就将凸 n 边形分割成三个区域，如图所示。其中区域 2 是一个三角形，区域 1 是一个凸 k 边形，拆分方案数是 F[k]，区域 3 是一个凸 n-k+1 边形，拆分方案数是 F[n-k+1]，此时的拆分方案总数为 F[k]F[n-k+1]，由于 p[k] 可以是 p[2]、p[3]、……、p[n-1]中 的任一点，由加法原理，凸 n 边形拆分总的方案数为 $\sum$F[i]F[n-i+1]，其中 1< i < n，边界条件为 h[2] = 1。

递推公式：$\sum_{2}^{n-1}F_iF_{n-i+1}$

递归进阶

在基础语法阶段，我们讲解的递归基本是给出数学推导式，更进一步，我们需要根据问题，判断是否应该使用递归解决。

如果确定需要递归解决，如何划分问题规模，使每一个递归过程都是独立的，问题规模向递减趋势发展，且有终止值。

且在递归过程中可能会出现大量重复计算，例如我们在基础语法阶段讲解过的递归求斐波那契数列，这个时候就可以使用记忆化存储，也叫做数组暂存优化，就是利用一个辅助数组T将计算过的结果保存起来，之后遇到$F_i$的值在数组中存储过，就直接使用T[i]的值，不需要继续递归计算。

例题：汉诺塔问题

题目描述

约19世纪末，在欧州的商店中出售一种智力玩具，在一块铜板上有三根杆，最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到中间的杆上，条件是一次只能移动一个盘，且不允许大盘放在小盘的上面。

这是一个著名的问题，几乎所有的教材上都有这个问题。由于条件是一次只能移动一个盘，且不允许大盘放在小盘上面，所以64个盘的移动次数是：18,446,744,073,709,551,615

这是一个天文数字，若每一微秒可能计算(并不输出)一次移动，那么也需要几乎一百万年。我们仅能找出问题的解决方法并解决较小N值时的汉诺塔，但很难用计算机解决64层的汉诺塔。

假定圆盘从小到大编号为1, 2, ...

输入

输入为一个整数(小于20）后面跟三个单字符字符串。

整数为盘子的数目，后三个字符表示三个杆子的编号。

输出

输出每一步移动盘子的记录。一次移动一行。

每次移动的记录为例如 a->3->b 的形式，即把编号为3的盘子从a杆移至b杆。

样例

2 a b c

a->1->c
a->2->b
c->1->b

解析：

那么如何把N个盘片从A柱移到B柱呢？

1.把上面的N-1个盘片从A移动到C

2.把第N个盘片从A移动到B

3.把上面的N-1个盘片从C移动到B

同时我们也需要注意到，对于递归来说可以把每一次递归看作是个阶段，如何选取递归的参数，可以参考表示阶段的变量。

如汉诺塔中第一个能想到的变量就是金片个数N，每个阶段的金片个数都会减一，是非常适合做参数的变量之一。