图的逻辑结构
图是由顶点及顶点间的关系(边)两个集合组成的数据结构,记作 G=(V , E)。
V:顶点的集合 E:边的集合
顶点间是多对多的关系
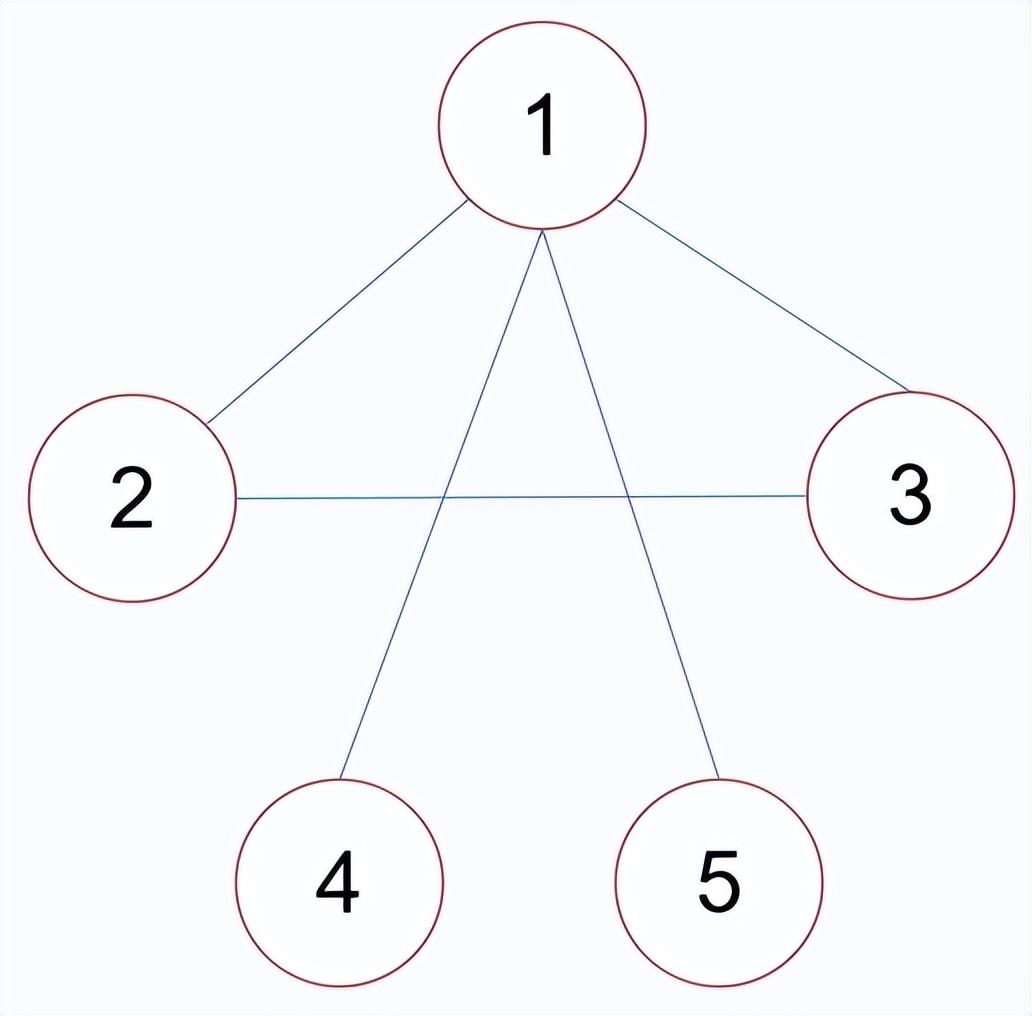
例:如下图中有顶点:
图:graph 顶点:vertex 边:edge
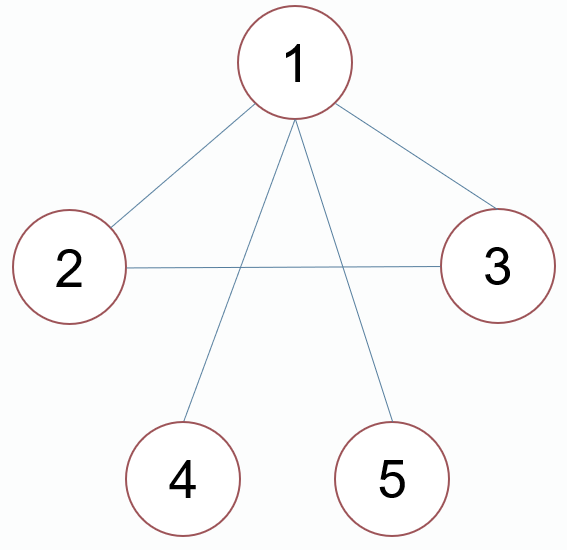
有向图:图中每一条边都是有方向的 有向边记为: 有向边,又称作:弧
例:该图有边
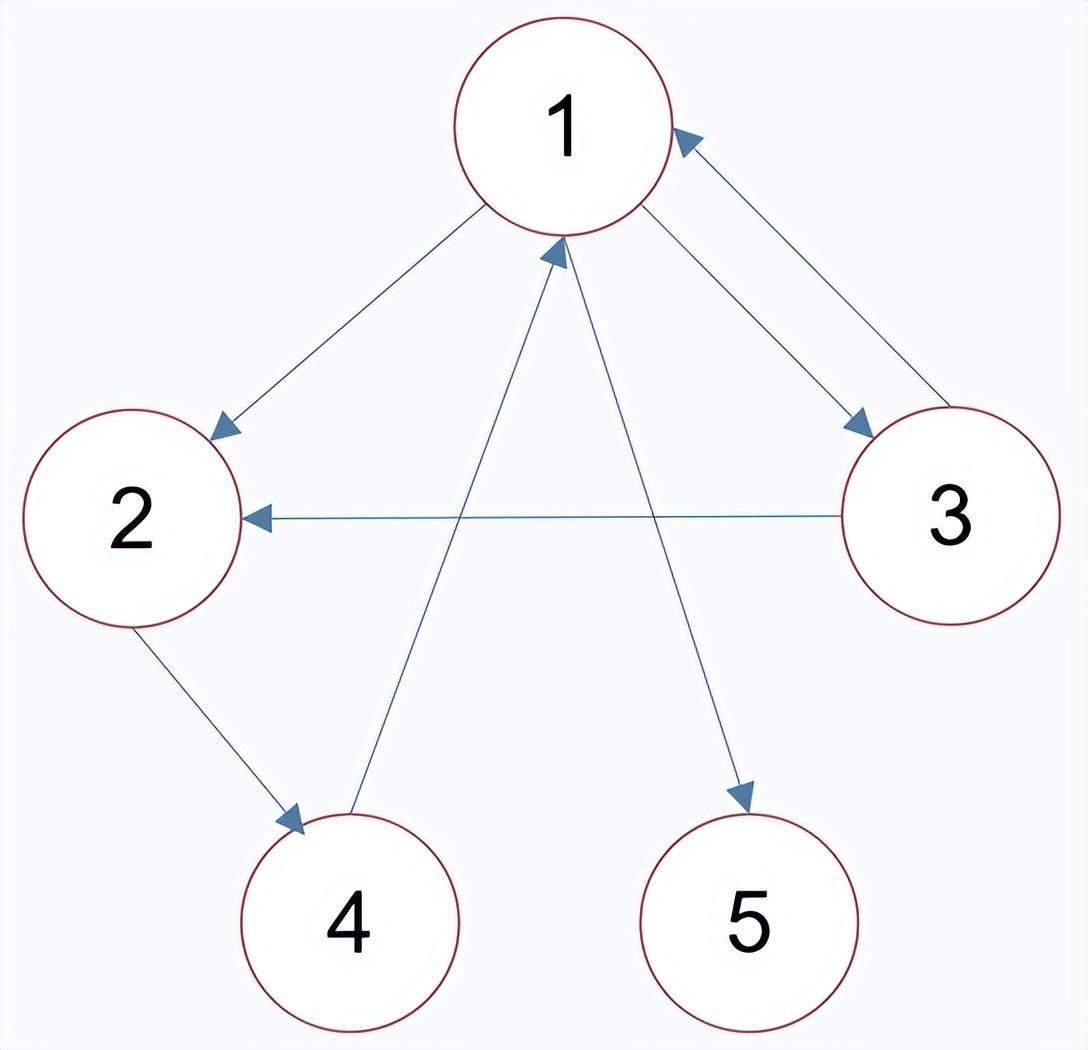
无向图:图中每一条边都是无方向的 无向边记为:
例:该图有边
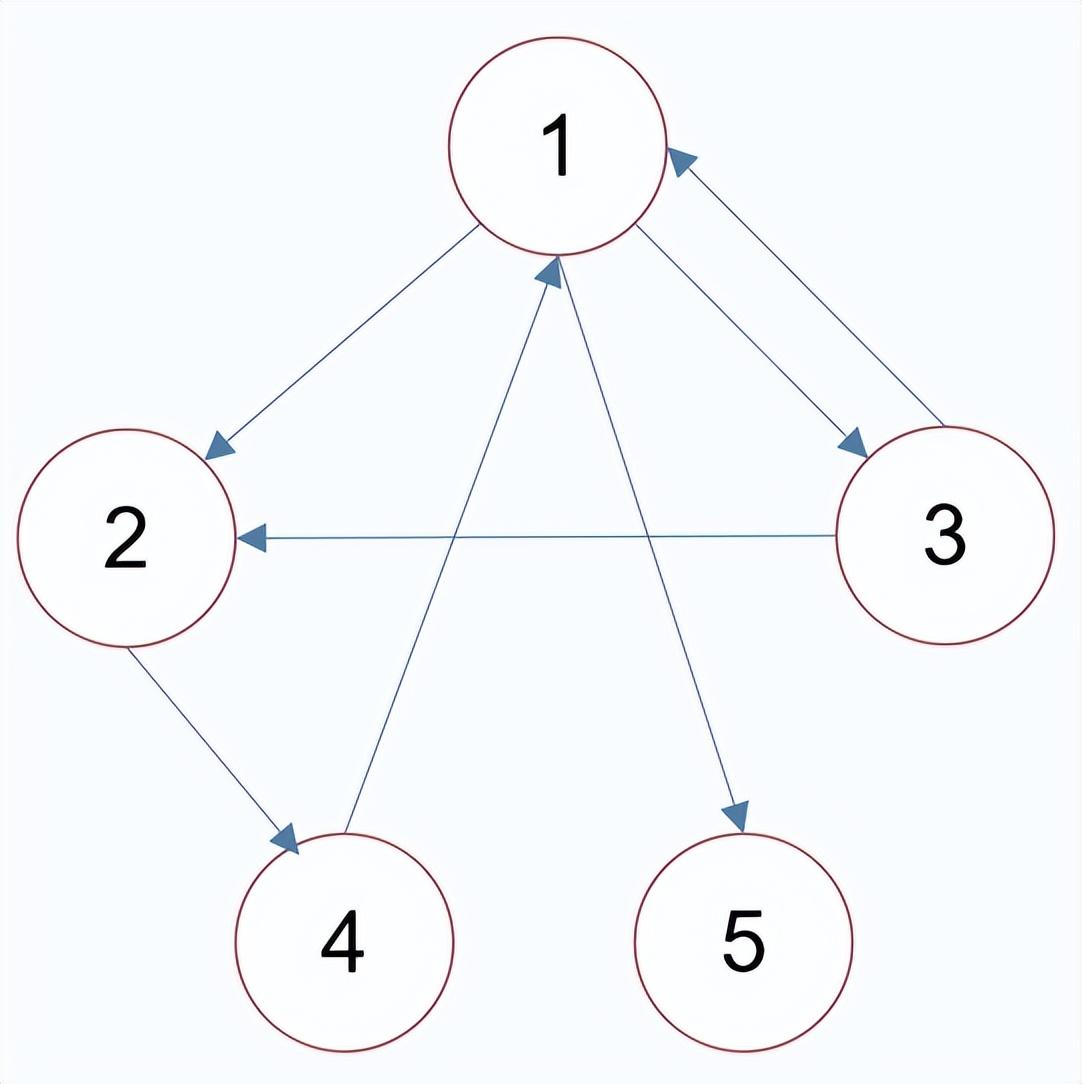
有向图中:
顶点的度:与该顶点相连的边的个数
入度:以该顶点为终点的边数 出度:以该顶点为起点的边数
顶点的度 = 入度 + 出度
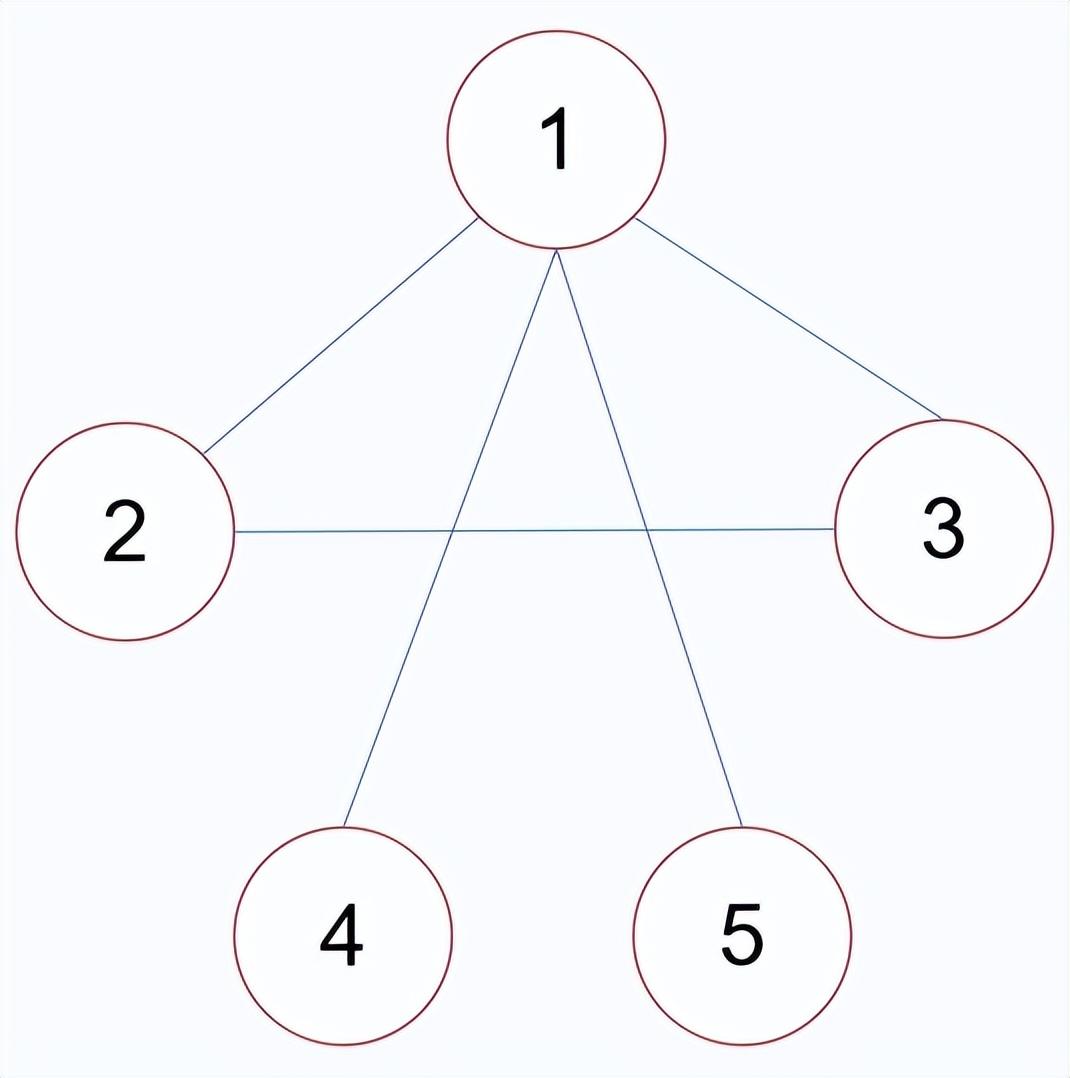
无向图中:
顶点的度:与该顶点相连的边的个数。
图的分类
对于图 G 有 V 个顶点 E 条边
稀疏图:边的条数 E 远小于 的图称为稀疏图
稠密图:边的条数 E 接近 的图称为稠密图
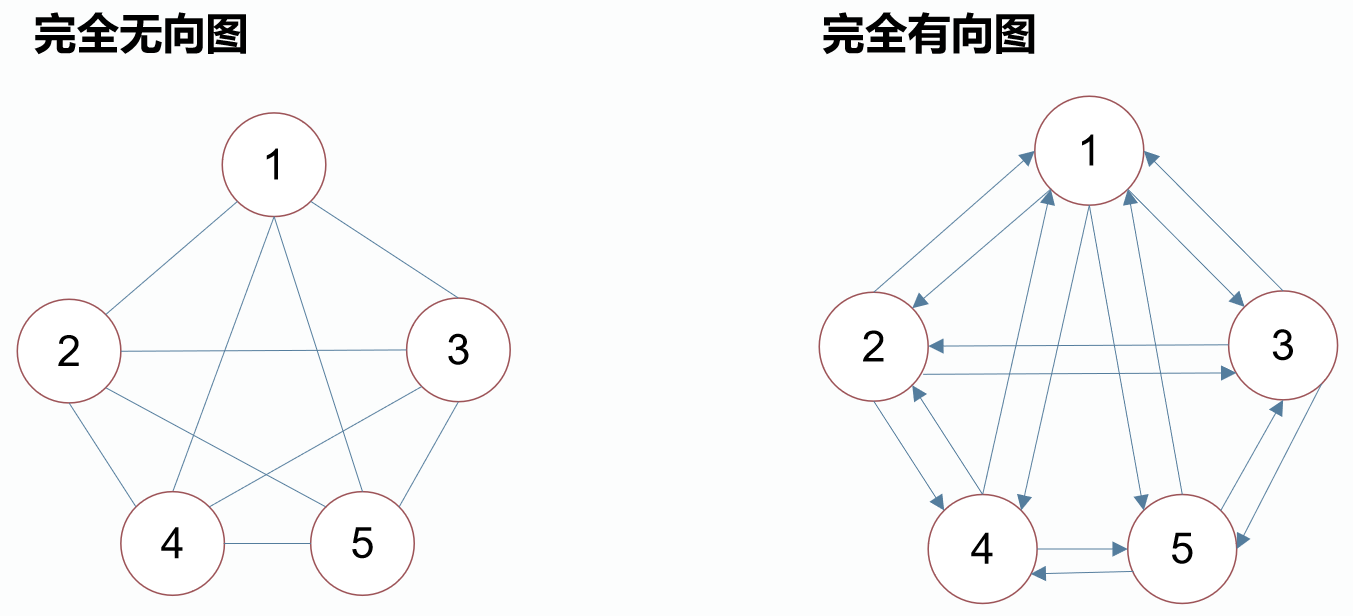
一个拥有n个结点的完全无向图的边数为:n×(n−1)÷2
一个拥有n个结点的完全有向图的边数为:n×(n−1)
路径
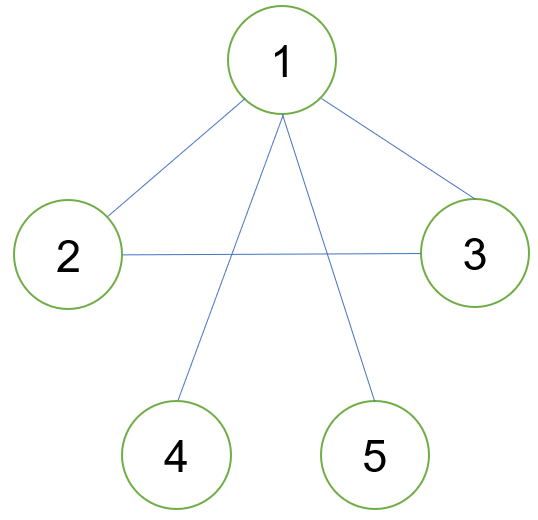
无向图中,顶点 到顶点 的路径是指存在一个顶点序列 ,其中 (, ) 均是该图的边。
例:从到的路径
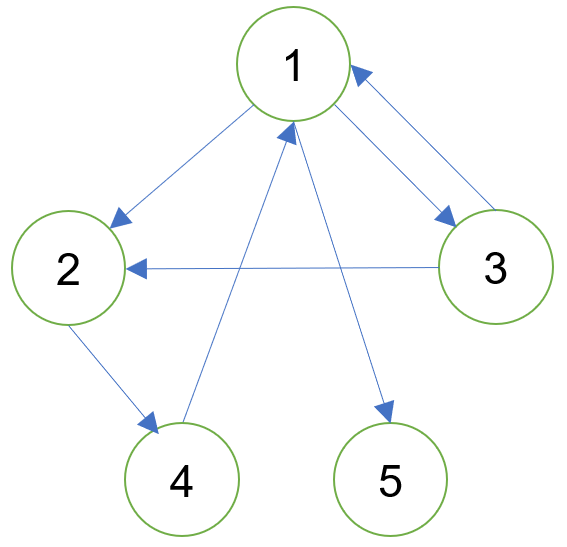
有向图中,顶点 到顶点 的路径是指存在一个顶点序列 ,其中 <, > 均是该图的边。
例:从到的路径
路径的长度:路径上边的数目。
简单路径:一条路径的顶点序列中的顶点各不相同。
例:
路径长度:3,是简单路径
路径长度:4,不是简单路径
某路径的顶点序列为 若 则该路称径为:回路或环
除第一个顶点和最后一个顶点相同外,其余顶点均不同,则称该回路为简单回路。
例: 是简单回路。
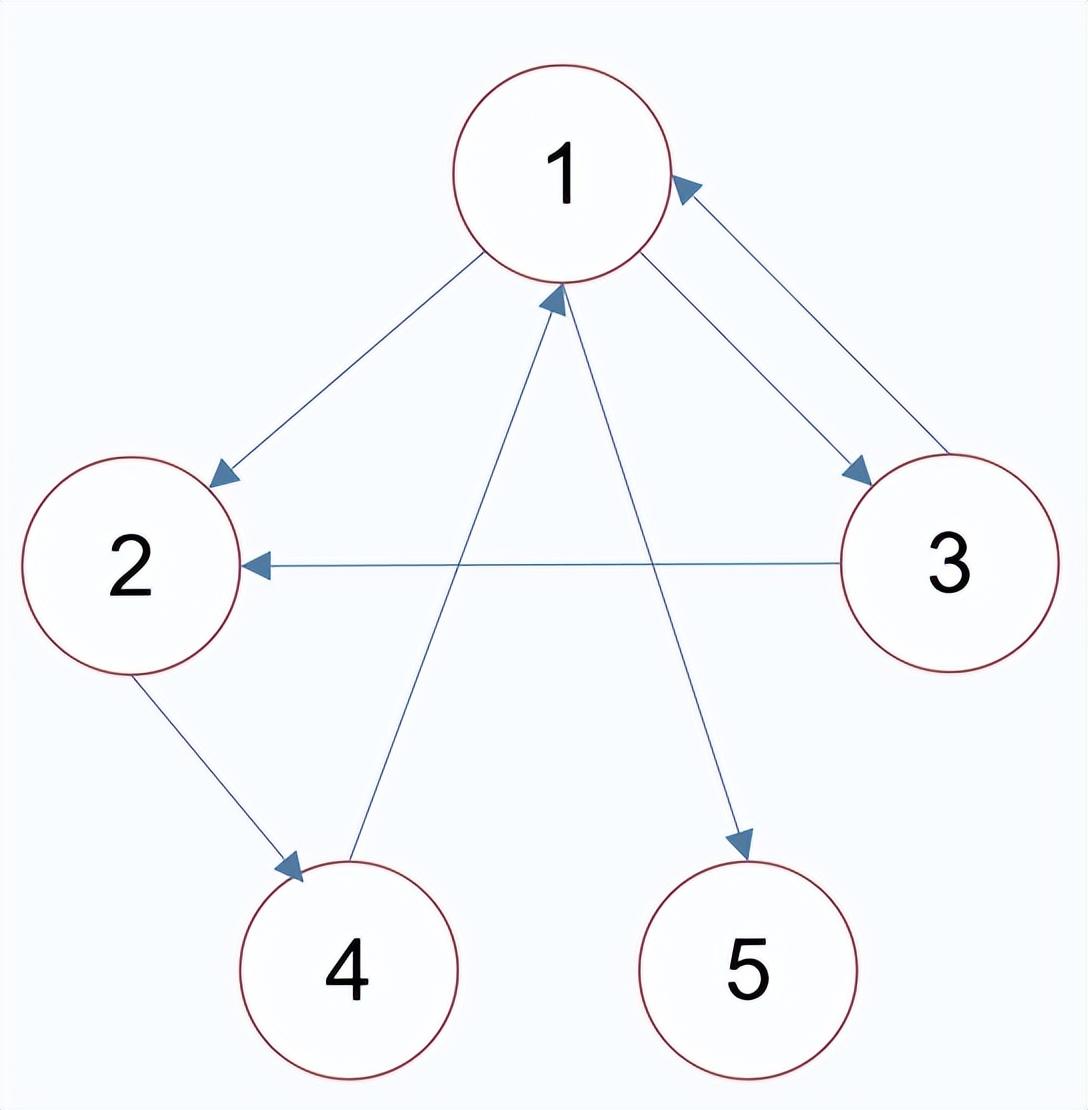
子图:图的部分顶点和边构成的图
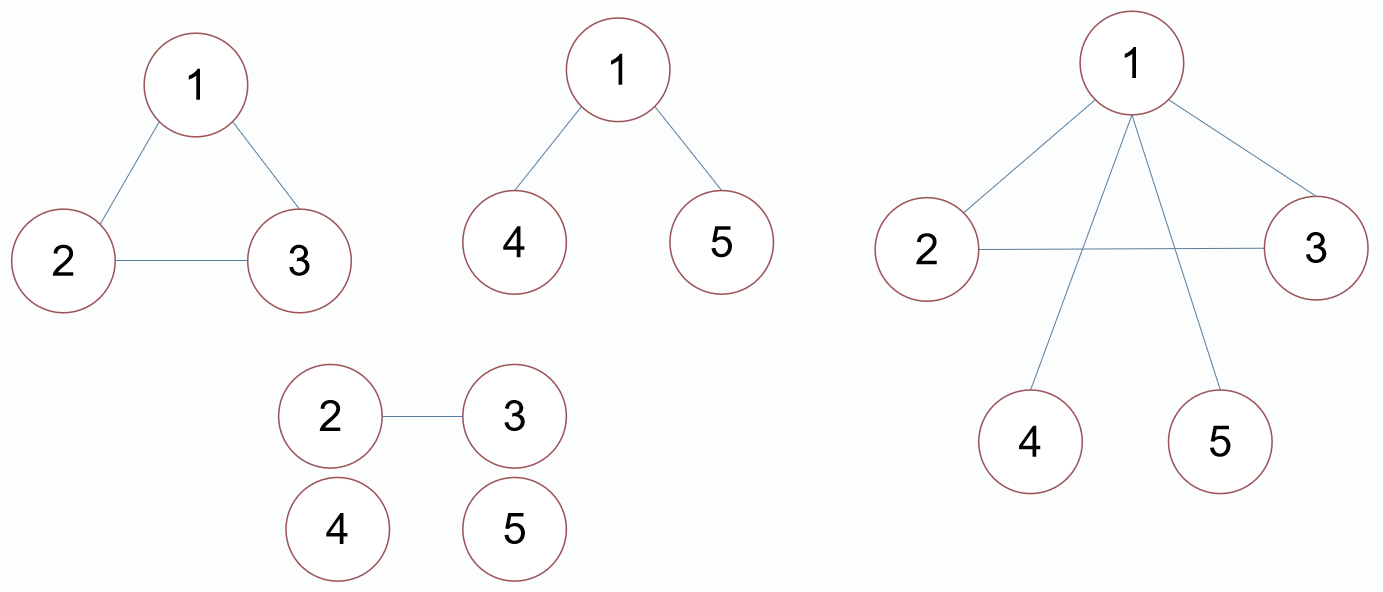
连通性
无向图的连通性:图中从一个顶点到达另一顶点,若存在至少一条路径,则称这两个顶点是连通的。
无向图中任意两个顶点之间都能够连通,则称此图为连通图。
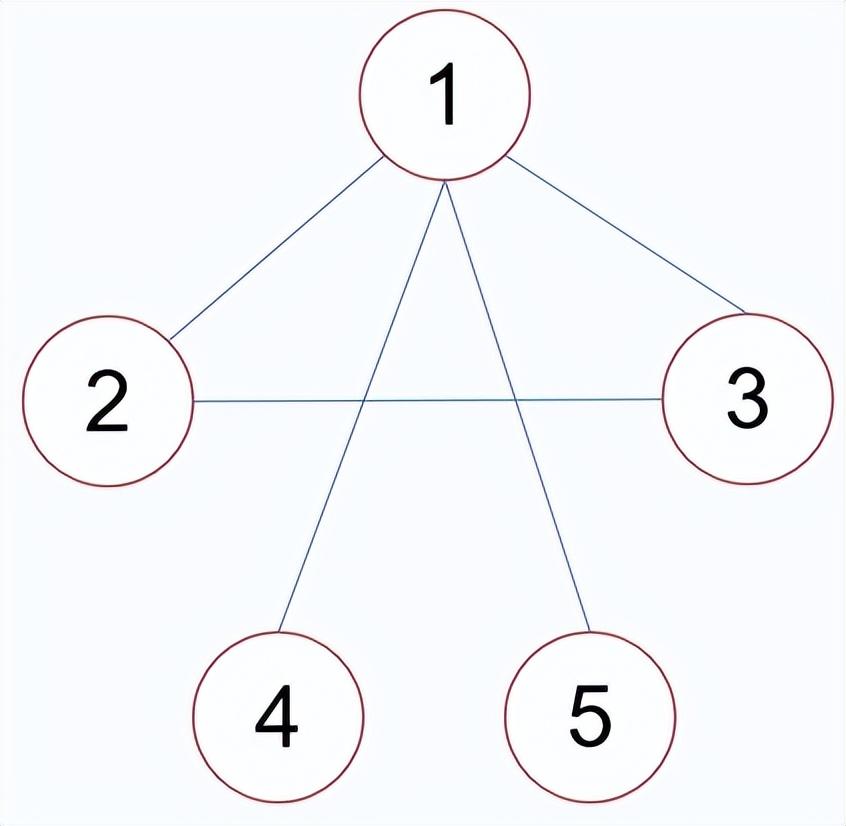
无向图的极大连通子图称为该图的连通分量。
极大连通子图说的是,如果将连通分量外的任意一个顶点添加进连通分量都会造成不连通。
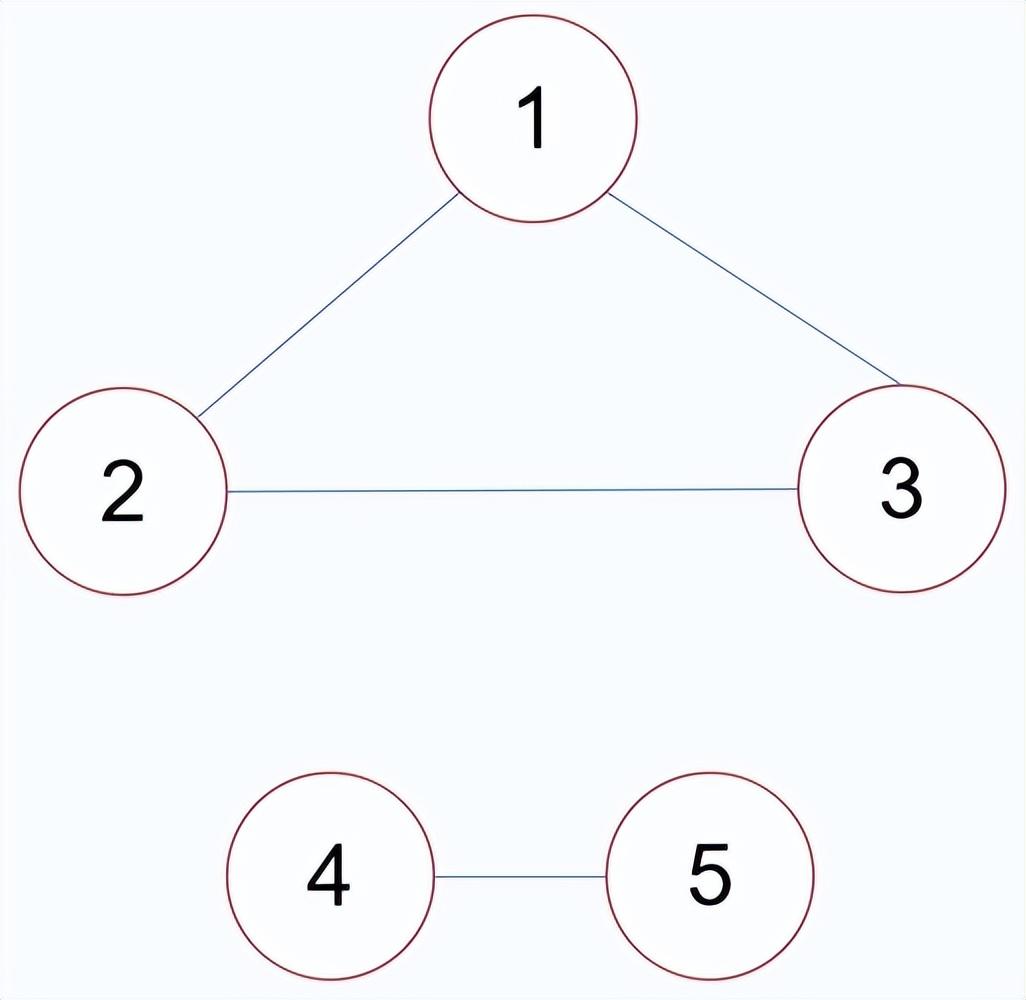
有向图中,若任意两个顶点 和 ,满足从 到 以及从 到 都连通,则称此有向图为强连通图。
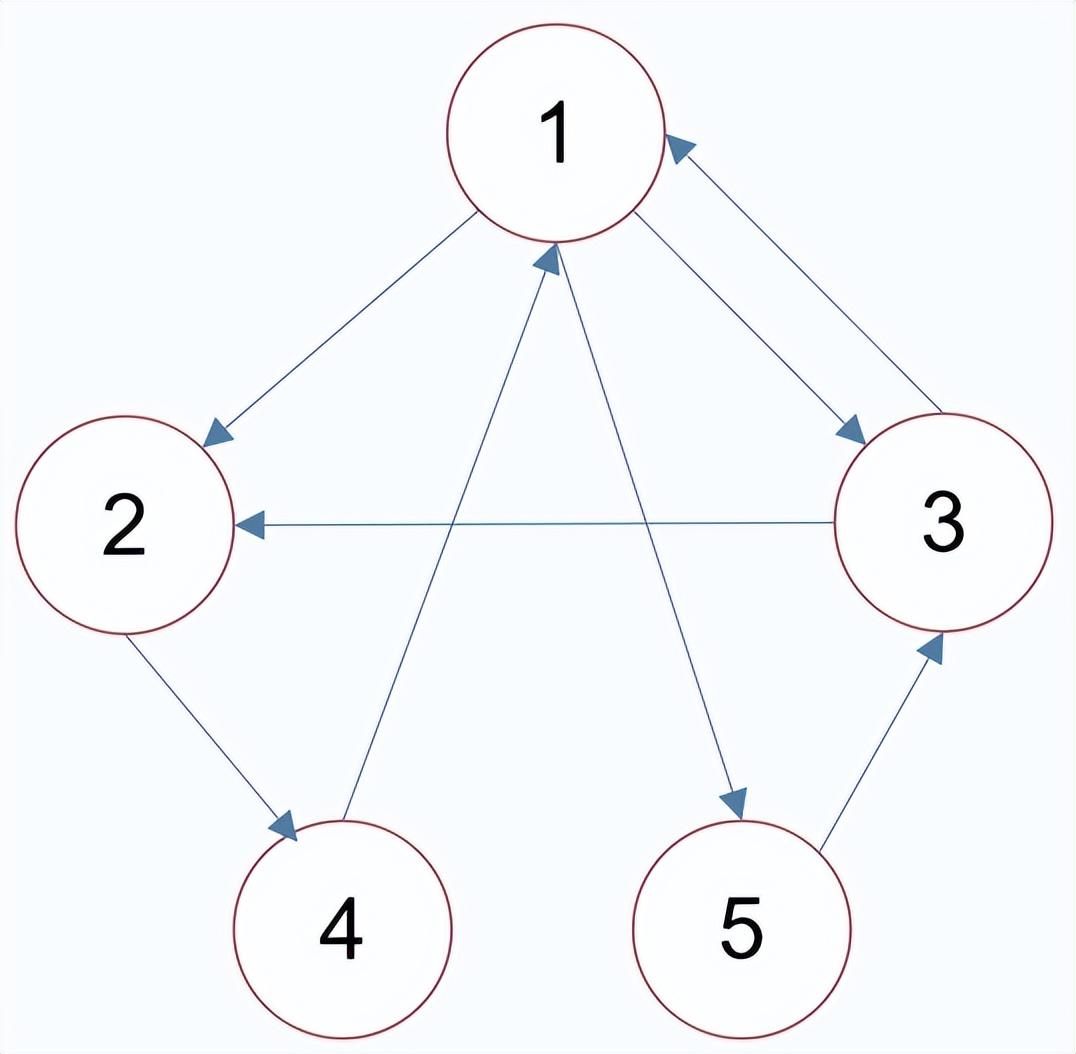
有向图的极大强连通子图,称为强连通分量。
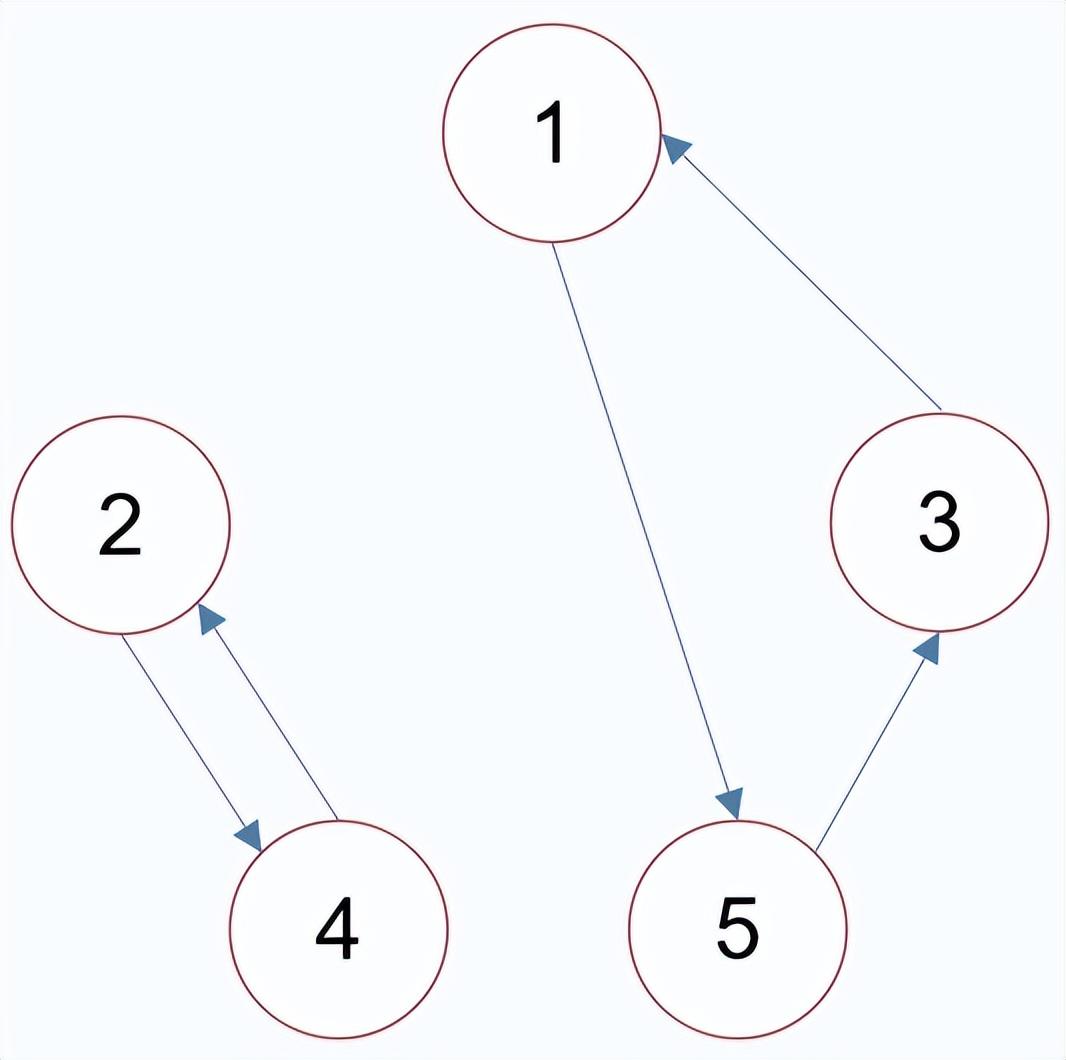
有向图中,若任意两个顶点 和 ,满足从 到 或从 到 连通,则称此有向图为单向连通图。
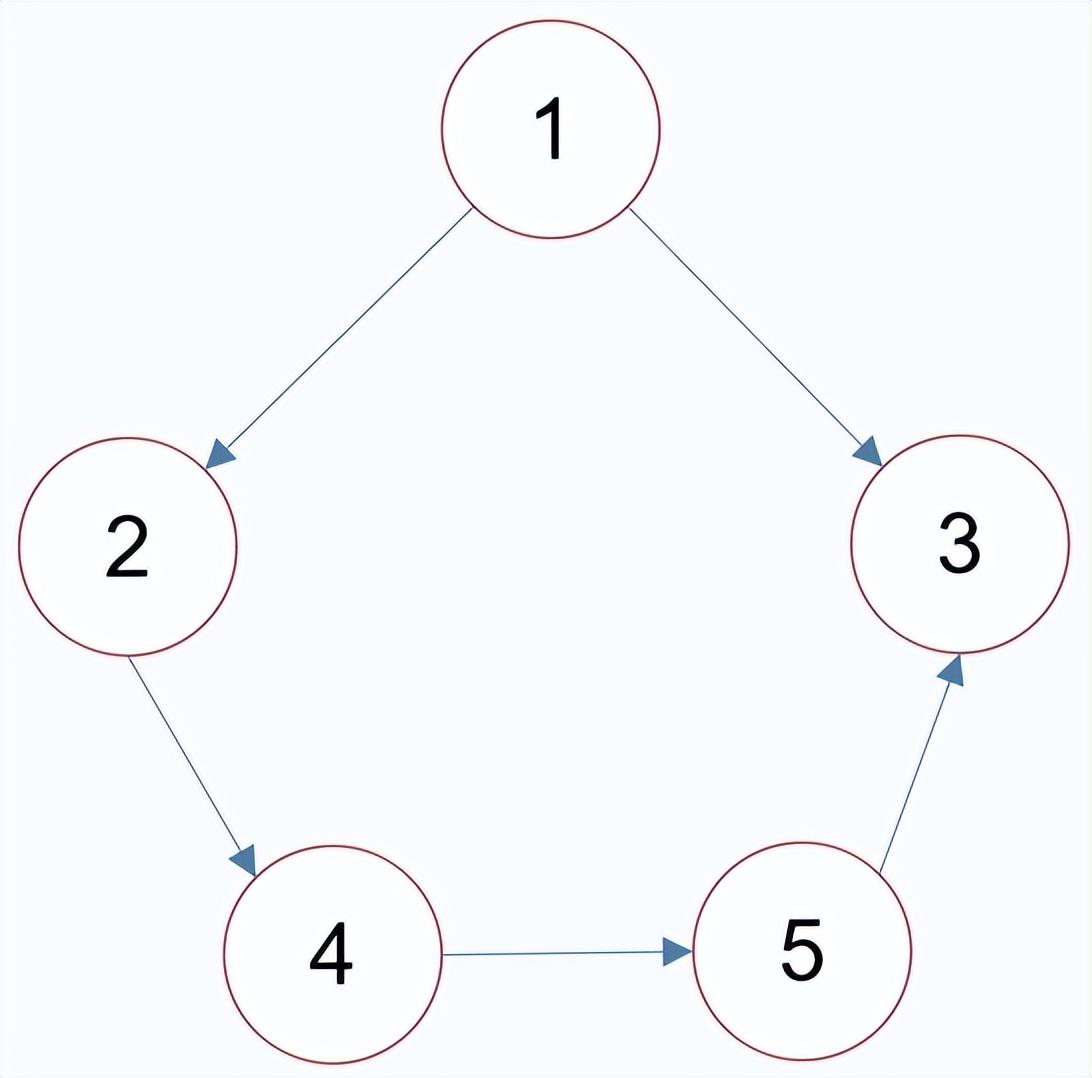
将有向图的所有的有向边替换为无向边,所得到的图称为原图的基图。如果一个有向图的基图是连通图,则有向图是弱连通图。

强连通图、单向连通图、弱连通图三者之间的关系:
强连通图属于单向连通图;
单向连通图属于弱连通图。
图的存储
邻接矩阵
设二维数组g, 若存在边 或 ,则g[i][j] = 1,否则,g[i][j] = 0
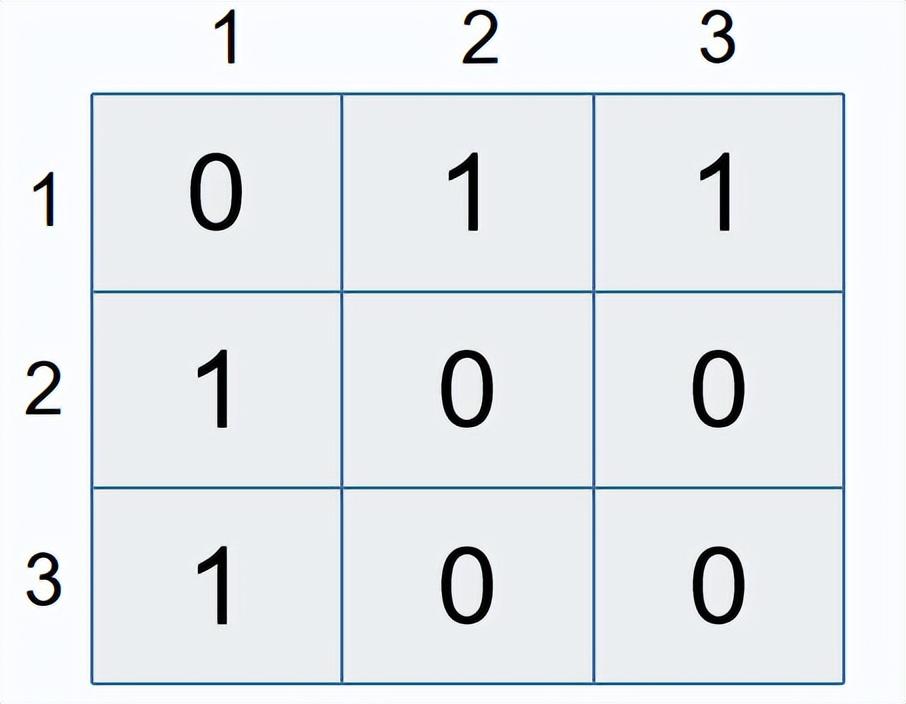
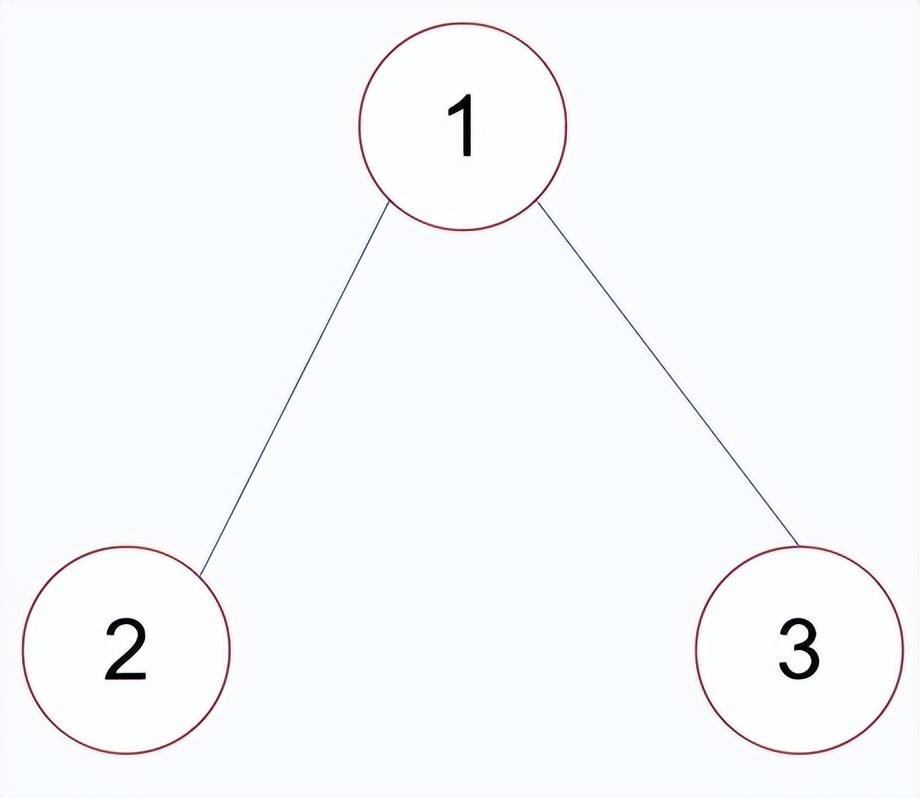
邻接矩阵的空间复杂度:
邻接矩阵适合表示稠密图。
邻接表
头结点数组:存储每个边链表第一个结点的地址
边链表:单链表中每个结点表示依附于该顶点的一条边
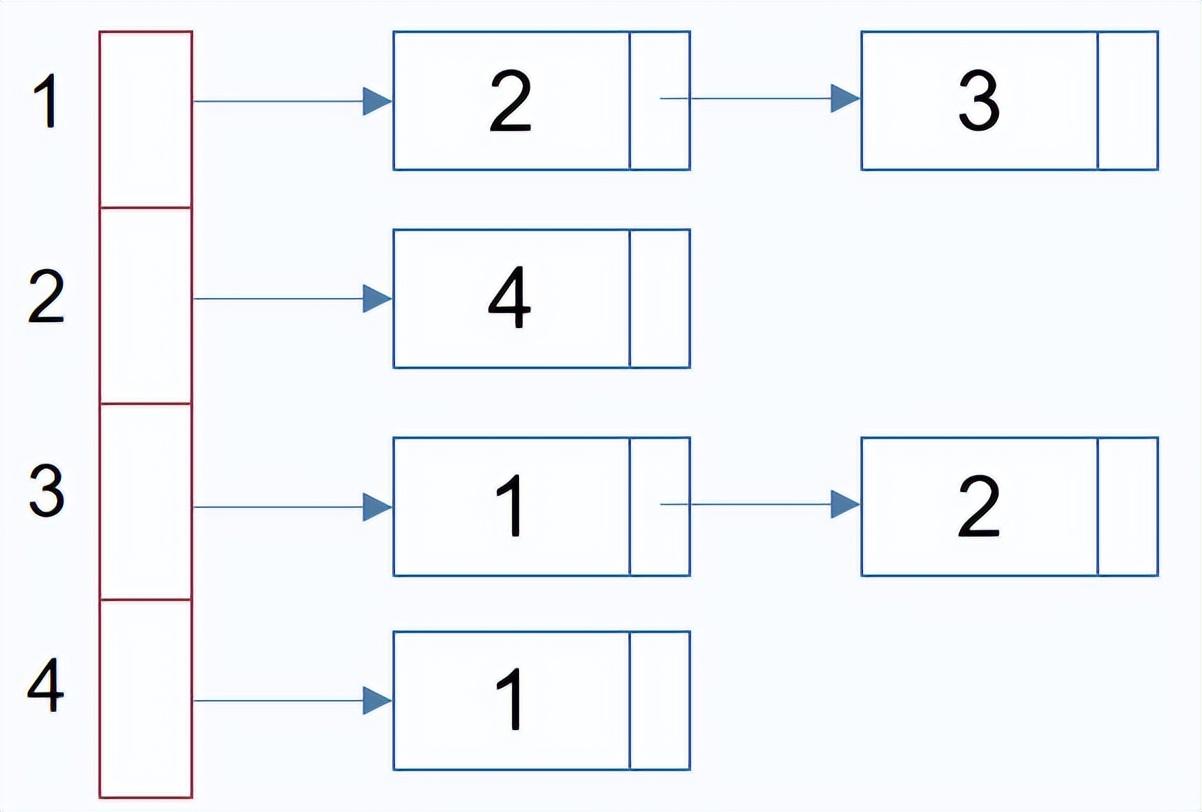
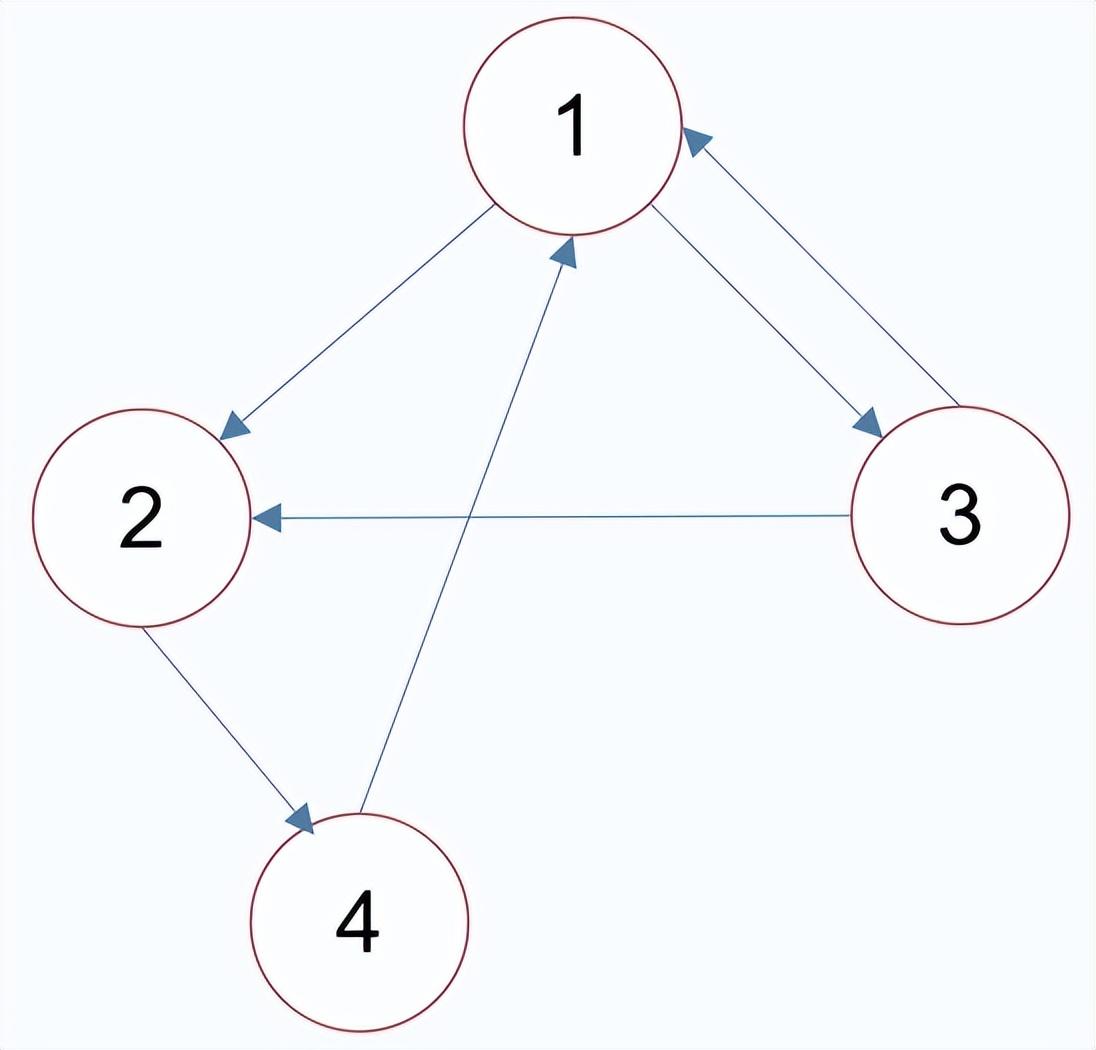
邻接表的空间复杂度:
邻接表适合表示稀疏图。
邻接表 vector数组
vector<int> h[N];//h[i]:顶点i的邻接点们
int n;//顶点总数
//无向图添加边(a,b)
h[a].push_back(b);
h[b].push_back(a);
//有向图添加弧<a,b>
h[a].push_back(b);
图的遍历
图的深度优先遍历

图的广度优先遍历
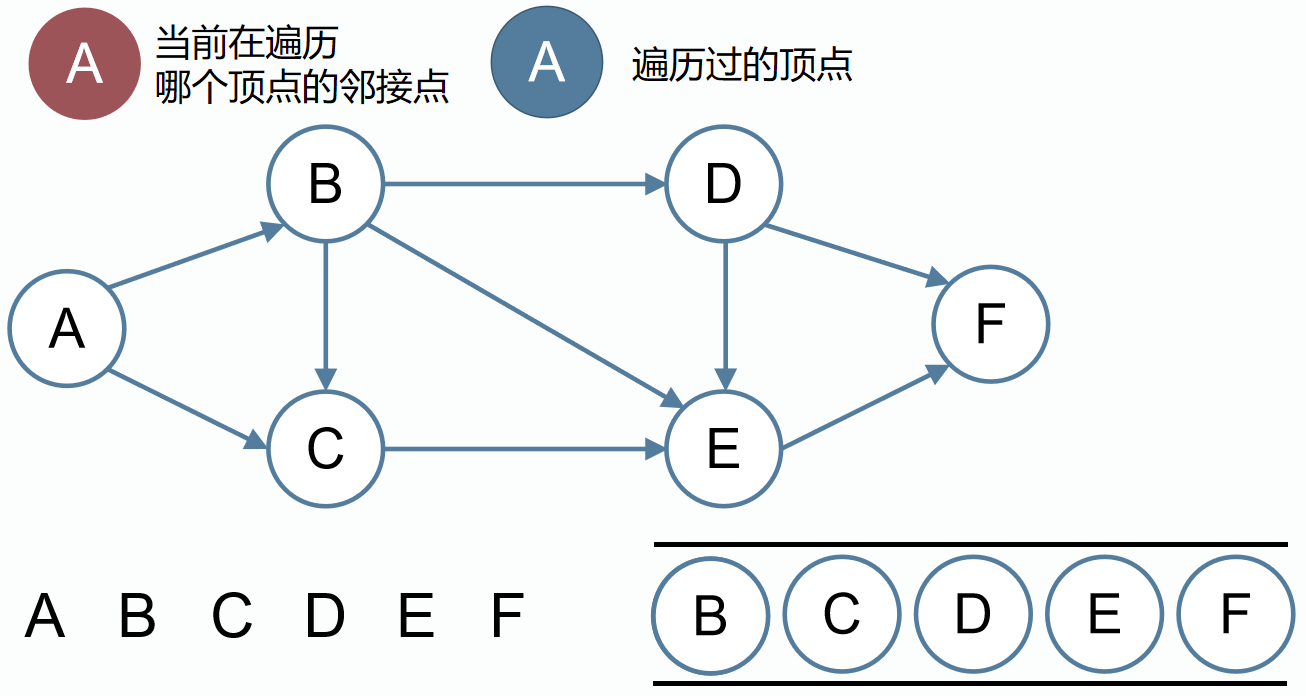
对图G=(V, E)进行深度优先遍历与广度优先遍历的时间复杂度为:
如果使用邻接矩阵:
如果使用邻接表: