为什么用高精度计算?
32 位计算机有符号整数(int)的取值范围是:

32 位计算机无符号整数(unsigned int)的取值范围是:

那么我们进一步思考,如果数据类型更大呢?可以使用 long long,但是还有没有更大的数据类型?
而所谓的高精度运算,是指在某些问题中,参与处理的数据大小超出了标准数据类型所能表示的范围的运算。
高精度运算是信息学比赛中用到的最基础的知识之一,单独考察的情形很少出现。但作为基础知识,在考察其他主要算法时会经常用到。且常出现在难度较高的题目中,要求选手具有较高的编程技巧和程序调试能力。
高精度存储
高精度数每一位数字存储在一个数组中。
例:请用字符数组方法输入两个高精度数 9753186420321
123456789

char s1[N], s2[N];
cin >> s1 >> s2;
cout << s1 << endl << s2 << endl;
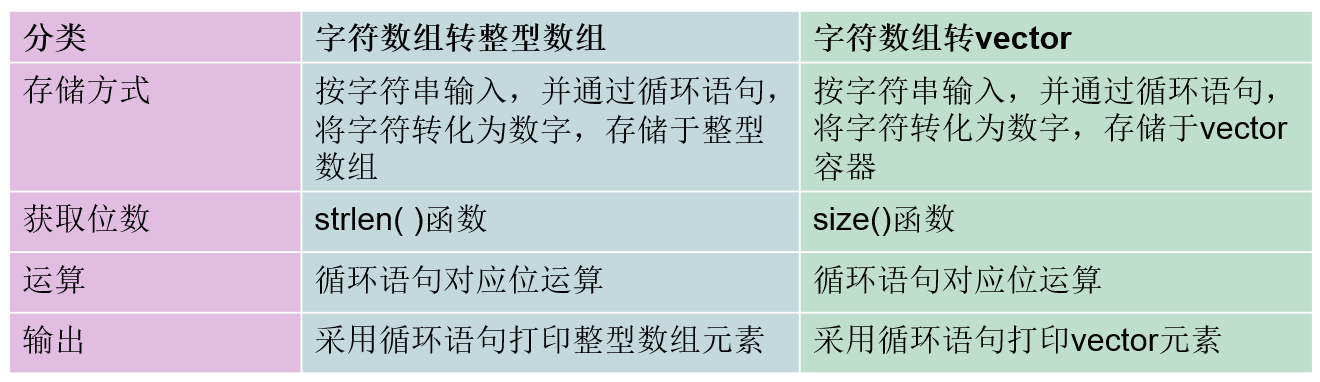
字符数组转整数数组:
方法一:前面元素从低位开始存储

方法二:前面元素存储大数低位,后面元素存储大数高位

方法三:第一个元素存储大数长度

然而,在我们实际解题过程中,经常是将高精度问题融入到一个其它类型算法当中,比如,高精度的斐波那契数列问题,就需要连续使用高精度加法,因此,我们将高精度算法都使用函数封装起来,参数和返回值都用vector类型,方便在各种情况下进行调用高精度运算。
高精度加法
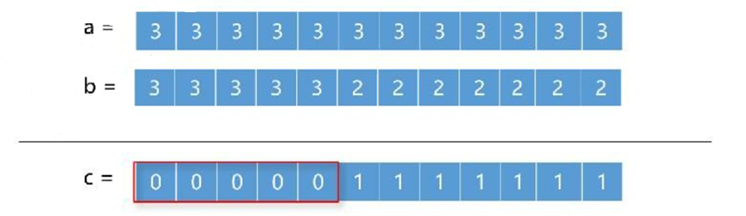
位数相同无进位
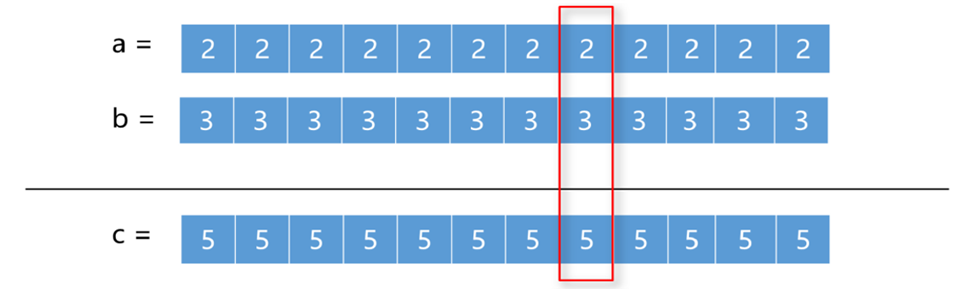
位数不同无进位
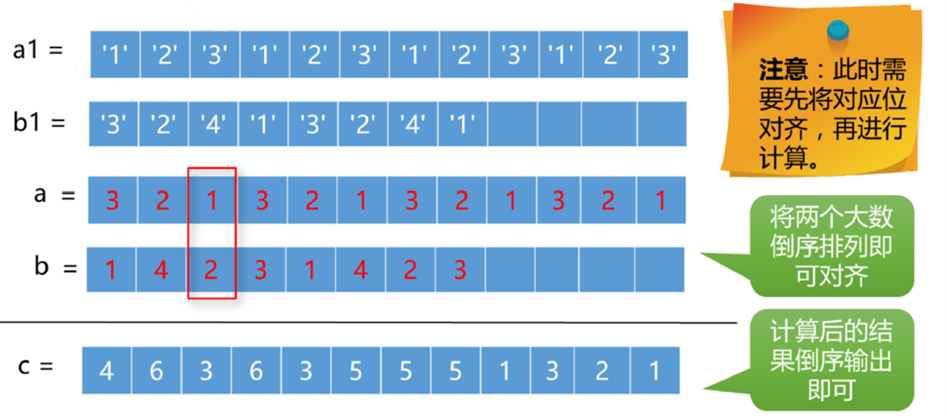
位数不同有进位

#include <iostream>
#include <string>
#include <vector>
using namespace std;
string str1, str2;
vector<int> A, B;
vector<int> add(vector<int>& A, vector<int>& B){
vector<int> C;
if(A.size() < B.size()) return add(B, A);
int k = 0; // 进位
for(int i = 0; i < A.size(); i++){
int t = A[i] + k;
if(i < B.size()) t += B[i];
C.push_back(t % 10);
k = t / 10;
}
if(k) C.push_back(1);
while(C.back() == 0 && C.size() > 1) C.pop_back();
return C;
}
int main(){
cin >> str1 >> str2;
for(int i = str1.size() - 1; i >= 0; i--) A.push_back(str1[i] - '0');
for(int i = str2.size() - 1; i >= 0; i--) B.push_back(str2[i] - '0');
auto C = add(A, B);
for(int i = C.size() - 1; i >= 0; i--)
cout << C[i];
return 0;
}
高精度减法
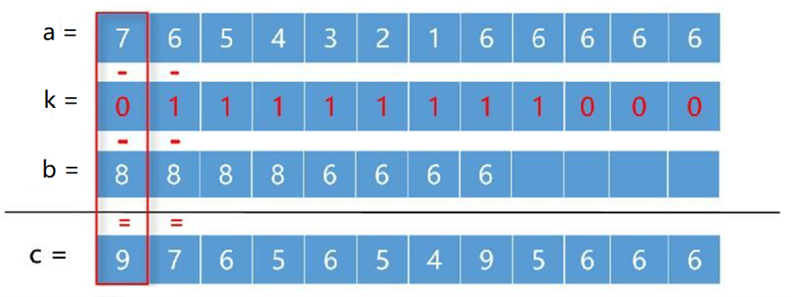
位数相同无借位
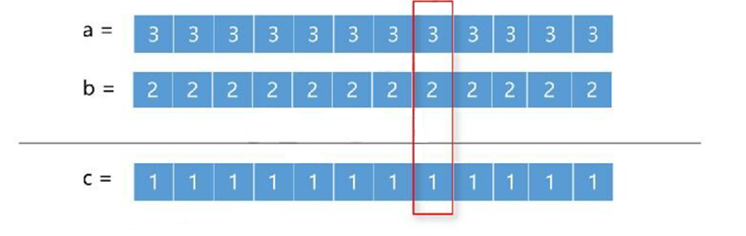
位数不同无借位

位数不同有借位
#include <iostream>
#include <cstdio>
#include <string>
#include <vector>
using namespace std;
string s1, s2;
vector<int> A, B, C;
bool cmp(vector<int>& A, vector<int>& B) {
if (A.size() != B.size()) return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; i--)
if (A[i] != B[i])
return A[i] > B[i];
return true;
}
vector<int> sub(vector<int>& A, vector<int>& B) {
vector<int> C;
if (!cmp(A, B)) {
cout << "-";
return sub(B, A);
}
int k = 0;
for (int i = 0; i < A.size(); i++) {
int t = A[i] - k;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) k = 1;
else k = 0;
}
while (!C.back() && C.size() > 1) C.pop_back();
return C;
}
int main() {
cin >> s1 >> s2;
for (int i = s1.size() - 1; i >= 0; i--) A.push_back(s1[i] - '0');
for (int i = s2.size() - 1; i >= 0; i--) B.push_back(s2[i] - '0');
C = sub(A, B);
for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
return 0;
}
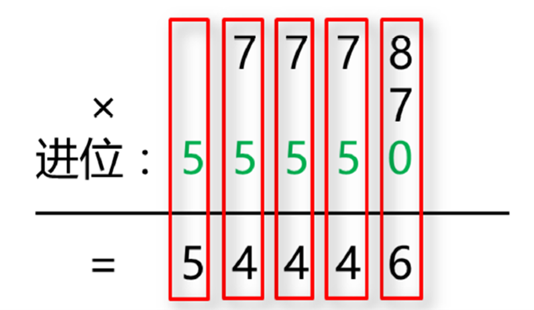
高精乘单精
高精度数字的每一位乘低精度数字,而后不断进位。
#include <iostream>
#include <cstdio>
#include <string>
#include <vector>
using namespace std;
string s1;
vector<int> A;
int b;
vector<int> mul(vector<int>& A, int b) {
vector<int> C;
int k = 0;
for (int i = 0; i < A.size() || k; i++) {
int t;
if (i < A.size()) t = A[i] * b + k;
else t = k;
k = t / 10;
C.push_back(t % 10);
}
while (!C.back() && C.size() > 1) C.pop_back();
return C;
}
int main() {
cin >> s1 >> b;
for (int i = s1.size() - 1; i >= 0; i--) A.push_back(s1[i] - '0');
vector<int> C = mul(A, b);
for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
return 0;
}
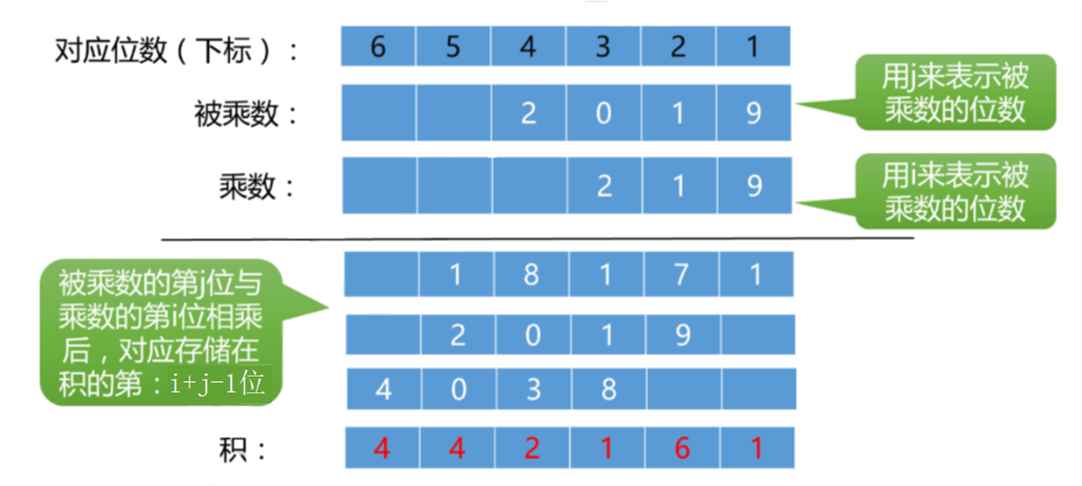
高精乘高精
#include <iostream>
#include <cstdio>
#include <vector>
#include <string>
using namespace std;
string s1, s2;
vector<int> A, B, C;
vector<int> mul(vector<int>& A, vector<int>& B) {
vector<int> C(A.size() + B.size() + 10);
for (int i = 0; i < B.size(); i++)
for (int j = 0; j < A.size(); j++)
C[i + j] += B[i] * A[j];
int t = 0;
for (int i = 0; i < C.size(); i++) {
t += C[i];
C[i] = t % 10;
t /= 10;
}
while (!C.back() && C.size() > 1) C.pop_back();
return C;
}
int main() {
cin >> s1 >> s2;
for (int i = s1.size() - 1; i >= 0; i--) A.push_back(s1[i] - '0');
for (int i = s2.size() - 1; i >= 0; i--) B.push_back(s2[i] - '0');
C = mul(A, B);
for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
return 0;
}
高精除单精

将商存储在 C 数组中,余数存储在变量 r 中。
#include <iostream>
#include <cstdio>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
string s1;
int b, r = 0;
vector<int> A;
vector<int> div(vector<int>& A, int b, int& r) {
vector<int> C;
for (int i = 0; i < A.size(); i++) {
int t = r * 10 + A[i];
C.push_back(t / b);
r = t % b;
}
reverse(C.begin(), C.end());
while (!C.back() && C.size() > 1) C.pop_back();
return C;
}
int main() {
cin >> s1 >> b;
for (int i = 0; i < s1.size(); i++) A.push_back(s1[i] - '0');
vector<int> C = div(A, b, r);
for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
// cout << endl << r << endl;
return 0;
}
高精除高精【选学】
#include <iostream>
#include <cstdio>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
string s1, s2;
vector<int> A, B, R;
bool cmp(vector<int>& A, vector<int>& B) {
if (A.size() != B.size()) return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; i--)
if (A[i] != B[i])
return A[i] > B[i];
return true;
}
vector<int> sub(vector<int> A, vector<int>& B) {
vector<int> C;
if (!cmp(A, B)) {
cout << "-";
return sub(B, A);
}
int k = 0;
for (int i = 0; i < A.size(); i++) {
int t = A[i] - k;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);
if (t < 0) k = 1;
else k = 0;
}
while (!C.back() && C.size() > 1) C.pop_back();
return C;
}
vector<int> div(vector<int>& A, vector<int>& B, vector<int>& R) {
vector<int> C;
int j = B.size();
R.assign(A.end() - j, A.end());
while (j <= A.size()) {
int k = 0;
while (cmp(R, B)) {
vector<int> tmp = sub(R, B);
R.assign(tmp.begin(), tmp.end());
k++;
}
C.push_back(k);
if (j < A.size()) R.insert(R.begin(), A[A.size() - j - 1]);
while (!R.back() && R.size() > 1) R.pop_back();
j++;
}
reverse(C.begin(), C.end());
while (!C.back() && C.size() > 1) C.pop_back();
return C;
}
int main() {
cin >> s1 >> s2;
for (int i = s1.size() - 1; i >= 0; i--) A.push_back(s1[i] - '0');
for (int i = s2.size() - 1; i >= 0; i--) B.push_back(s2[i] - '0');
if(!cmp(A, B)){
cout << 0 << endl;
cout << s1 << endl;
return 0;
}
vector<int> C = div(A, B, R);
for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
cout << endl;
for (int i = R.size() - 1; i >= 0; i--) cout << R[i];
return 0;
}