找伪币

给出 16 个一模一样的硬币，其中有一个是伪造的，伪造的硬币比真的硬币要轻一些。任务为找出伪造的硬币。提供一台可以用来比较两组硬币的仪器，利用仪器可以知道两组硬币谁轻谁重。

方法1：暴力枚举。

一次比较硬币 1 与硬币 2、硬币 3…..最多通过 8 次比较来找出伪币。

方法2：二分法。

把 16 个硬币的情况看成一个大问题，把大问题分成两个小问题。

把 16 个硬币分成 8 个和 8 个（两组）。之后对比两组重量，找出轻的 8 个；

再把 8 个硬币分成 4 个和 4 个（两组）。之后对比重量，找出轻的 4 个；

再把 4 个硬币分为 2 个和 2 个（两组）。之后对比重量，找出轻的 2 个；

再把 2 个硬币分为 1 个和 1 个（两组）。找出伪币。

这样只需要 4 次比较就可以找出伪币。

方法3：三分法。

把 16 个硬币分成 3 组（5，5，6）用仪器比较两组一次就能得出伪币在哪一组；

假设在第三组，6 个硬币再分成（2，2，2）再比较一次就知道在哪一组；

最后 2 个硬币再进行比较即可，这样只需要 2~3 次即可找出伪币。

分治的思想，将较大规模的问题分解成几个较小规模的问题，通过对较小规模问题的求解达到对整个问题的求解。当将问题分解成两个较小问题求解时的分治方法称之为二分法（也是较为常用的分治方法）。

二分查找

二分查找（也叫折半查找），是一种在有序序列上的查找算法。

查找思路：

对于有序数列（从小到大），设定左端 L（最小元素下标）和右端 R（最大元素下标）

当满足条件 L<=R 时，求中点 mid，将中点元素的值与所要查找的值比较。

若中点元素值比所要查找元素小，则应找后半段，所以 L = m+1。
否则应找前半段 R = m - 1，直到找到为止。
若 L > R，则说明找不到。

问题 1：升序数组，各元素不同，查找某元素。

如果该元素存在：输出该元素的下标；

如果不存在该元素，输出 -1。

在数字序列中 1 3 4 6 7 9 11 16 23 45，查找 11 的位置。

问题1：升序数组，各元素不同，查找某元素。

如果该元素存在：输出该元素的下标；

如果不存在该元素，输出 -1。

在数字序列中 1 3 4 6 7 9 11 16 23 45，查找 11 的位置：

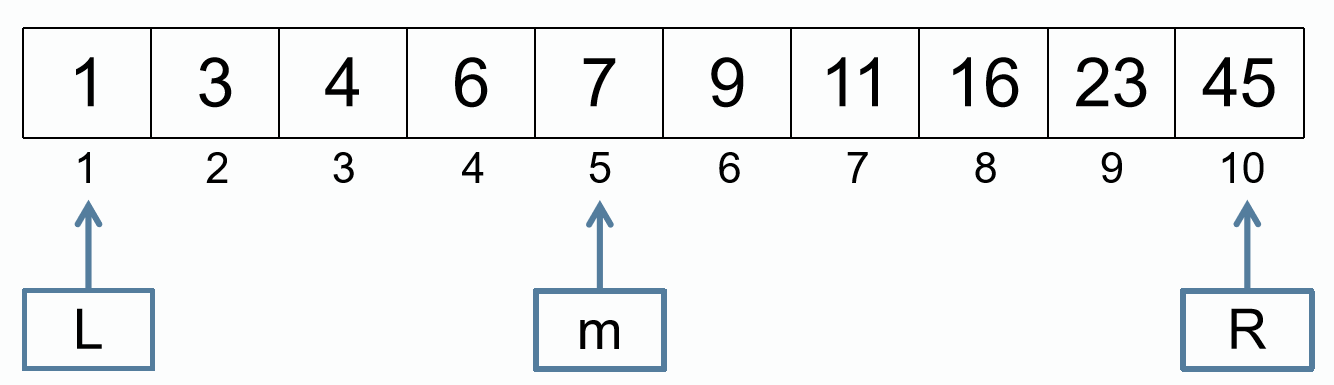
m = (L + R) / 2
L = m + 1

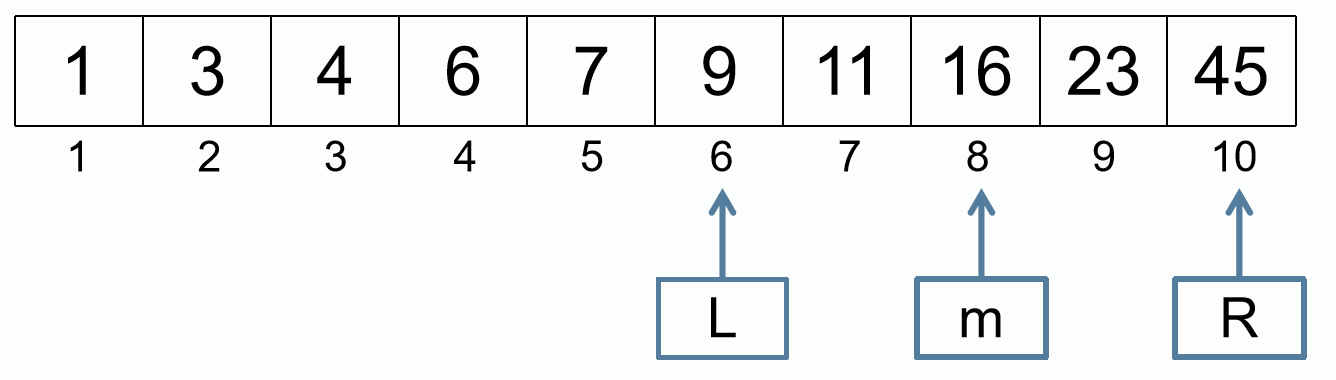
m = (L + R) / 2
R = m - 1

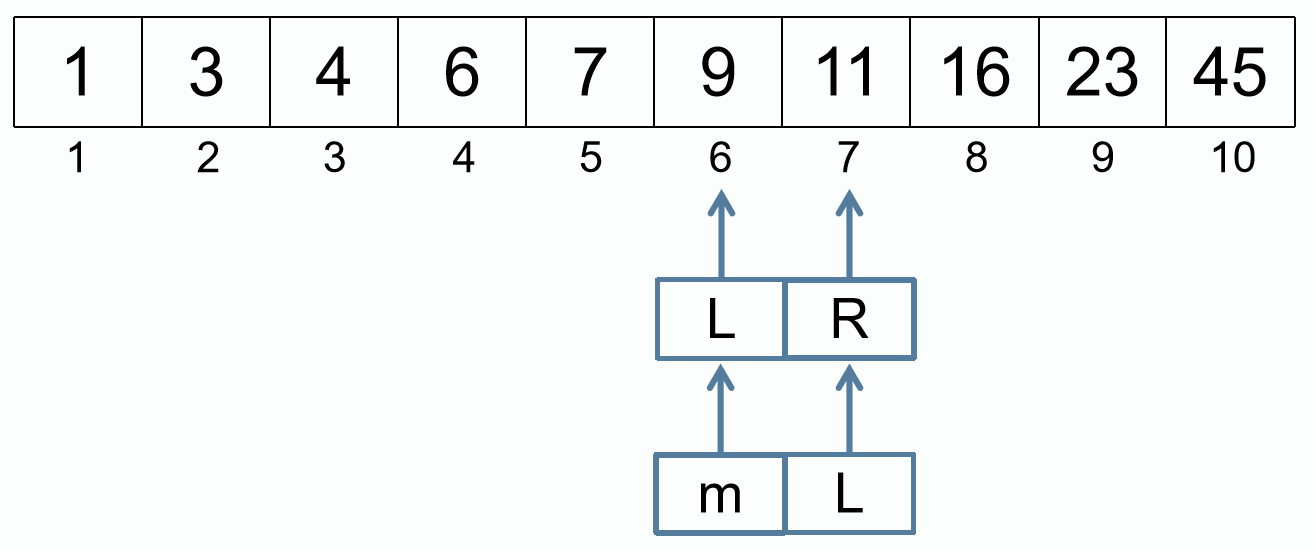
m = (L + R) / 2
L = m + 1

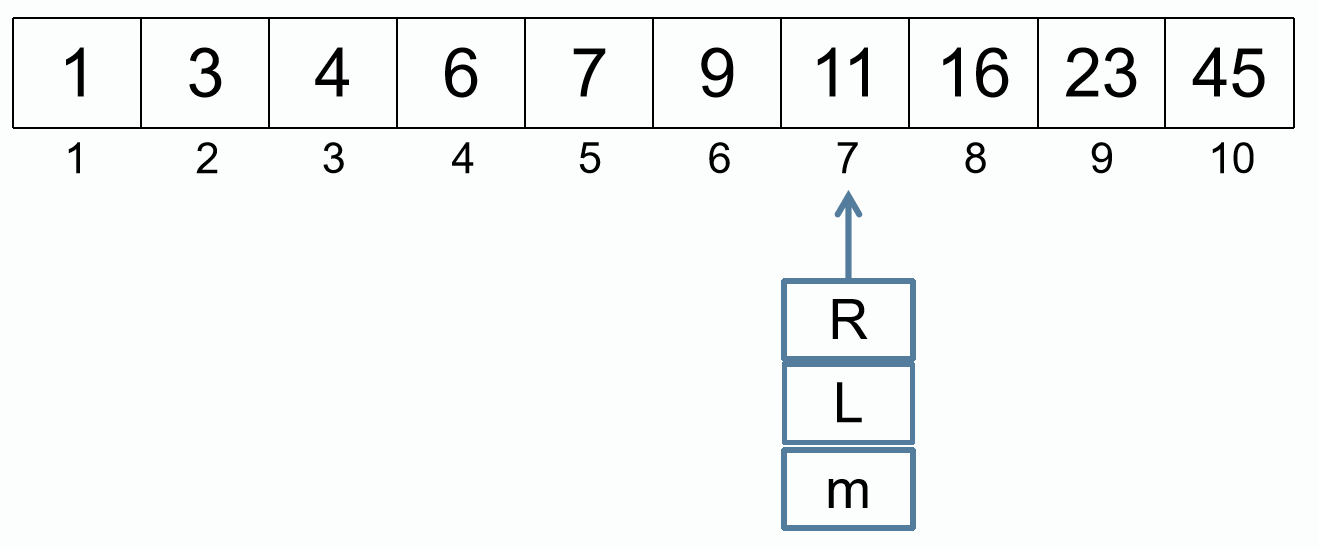
m = (L + R) / 2

找到 11 的位置是 7。

查找 10 的位置

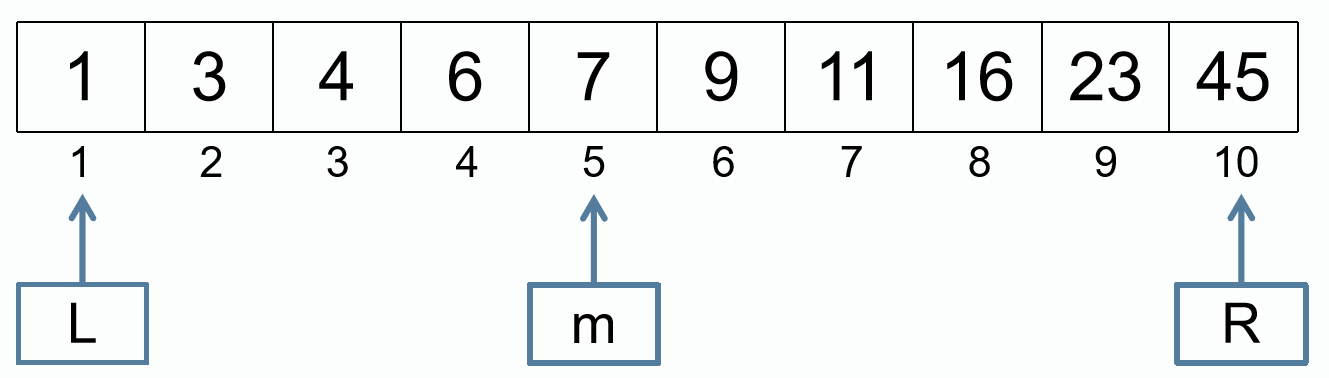
m = (L + R) / 2
R = m - 1

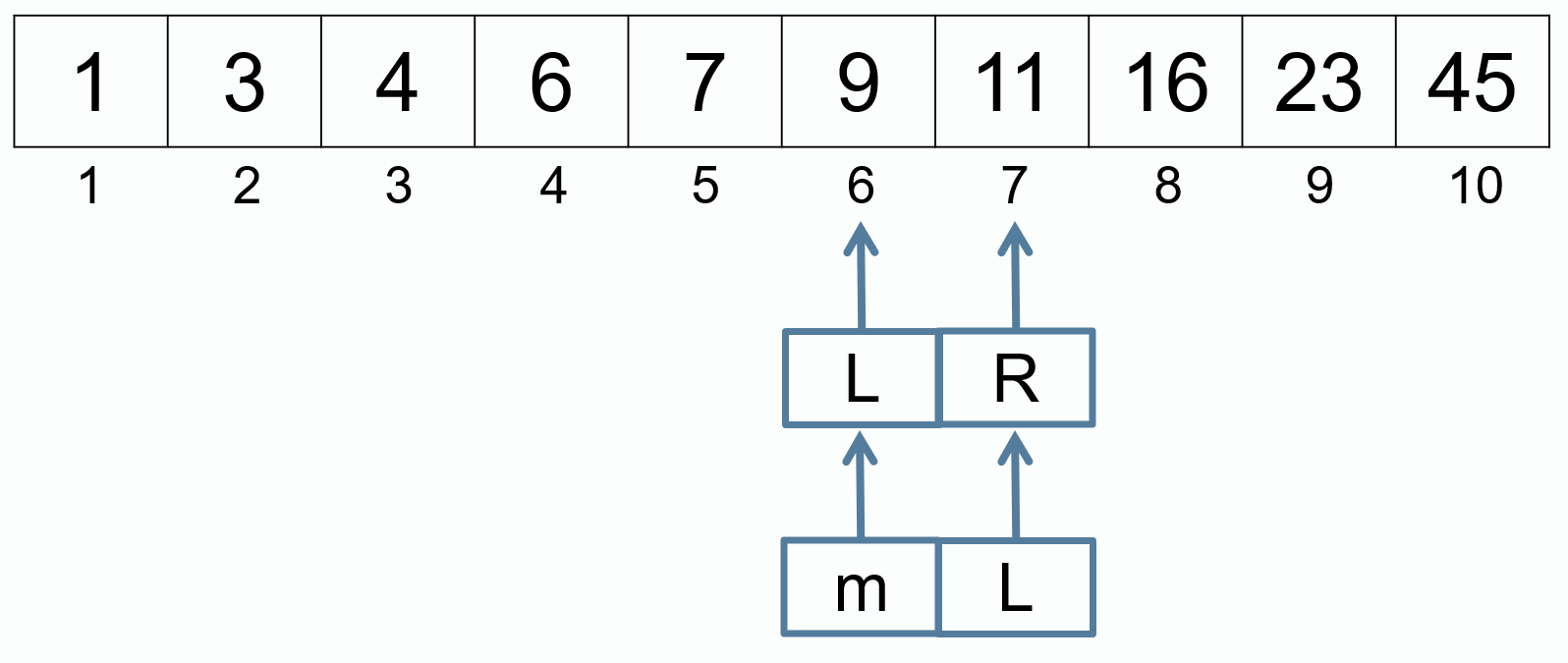
m = (L + R) / 2
L = m + 1

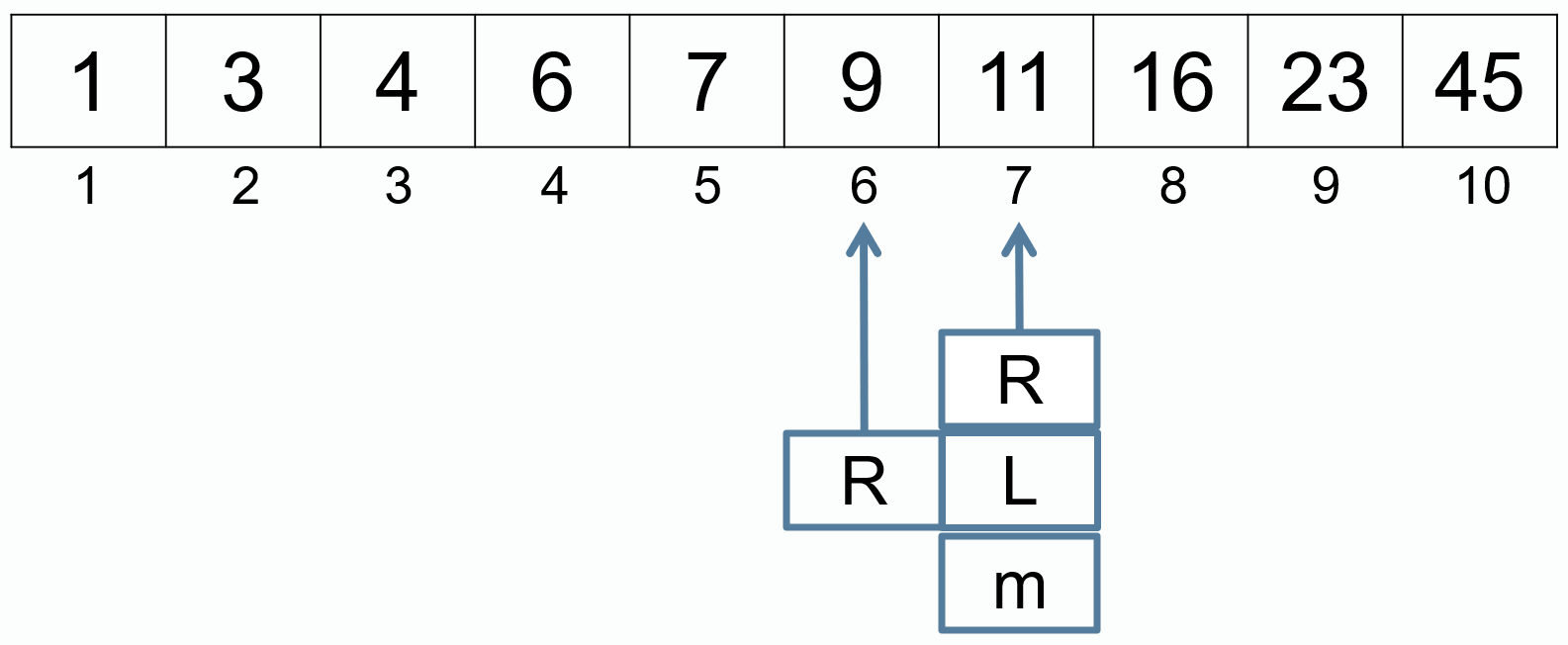
m = (L + R) / 2
R = m - 1

不再满足 L <= R，查找结束，没有找到。

在 n 个元素的有序序列中进行二分查找：

最大比较次数：⌊log2n⌋+1
时间复杂度：O(logn)

例题：查找存在性

设有N个数已经按从大到小的顺序排列，现在输入X，判断它是否在这N个数中，如果存在则输出YES 否则输出NO。

方案1：使用顺序查找

#include <iostream>
using namespace std;

const int N = 1e5 + 10;

int n, x;
int a[N];

int main() {

    cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i];
    cin >> x;

    for(int i = 1; i <= n; i++){
        if(a[i] == x){
            cout << "YES" << endl;
            return 0;
        }
    }

    cout << "NO" << endl;

    return 0;
}

方案2：二分查找模板

int L = 1, R = n;

while(L <= R){
    int m = L + R >> 1;
    if(a[m] == x){
        cout << "YES" << endl;
        return 0;
    }

    if(a[m] > x) L = m + 1;
    else R = m - 1;
}

cout << "NO" << endl;

方案3：使用二分库函数

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1e5 + 10;

int n, x;
int a[N];

class Cmp {
public:
    bool operator()(const int& a, const int& b) {
        return a > b;
    }
};

int main() {

    cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i];
    cin >> x;

    bool ret = binary_search(a + 1, a + n + 1, x, Cmp());

    if(ret) cout << "YES" << endl;
    else cout << "NO" << endl;

    return 0;
}

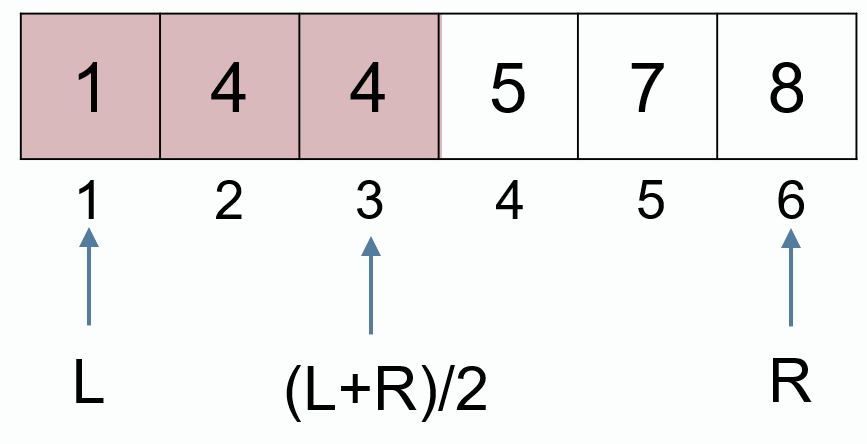
问题2：升序数组，各元素可能相同，查找大于等于 x 的最小值的最小下标。

如果该元素存在：输出该元素最后一次出现的下标
如果不存在该元素，输出 -1，例如查找 4

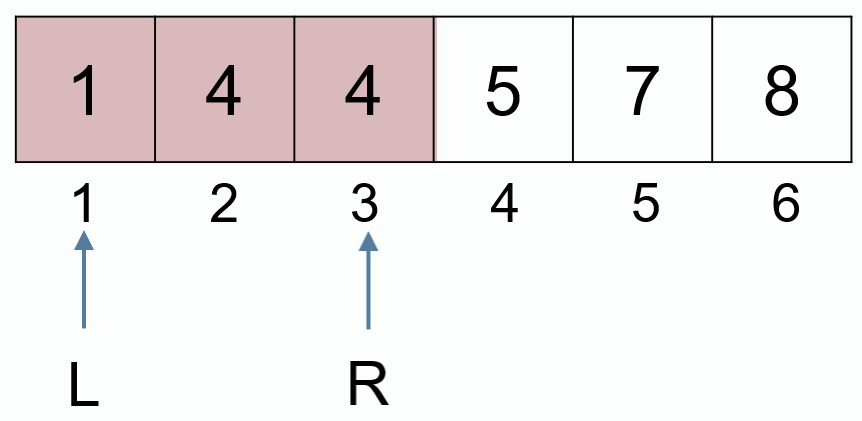
问题3：升序数组，各元素可能相同，查找小于等于 x 的最大值的最大下标。

如果该元素存在：输出该元素最后一次出现的下标
如果不存在该元素，输出 -1，例如，查找 7

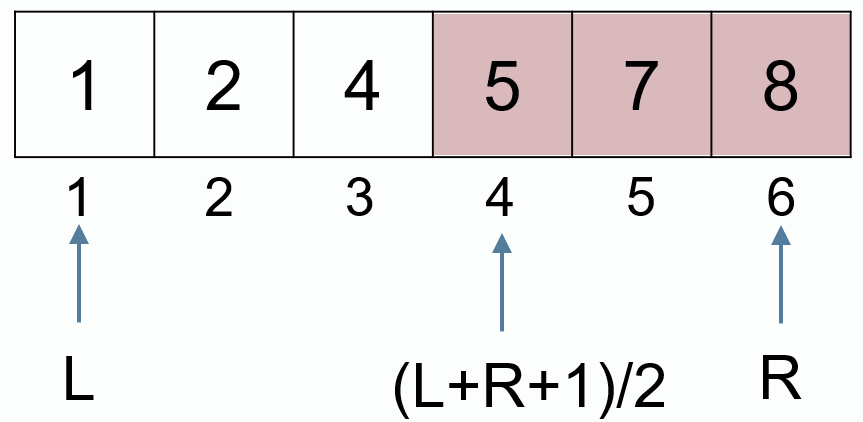
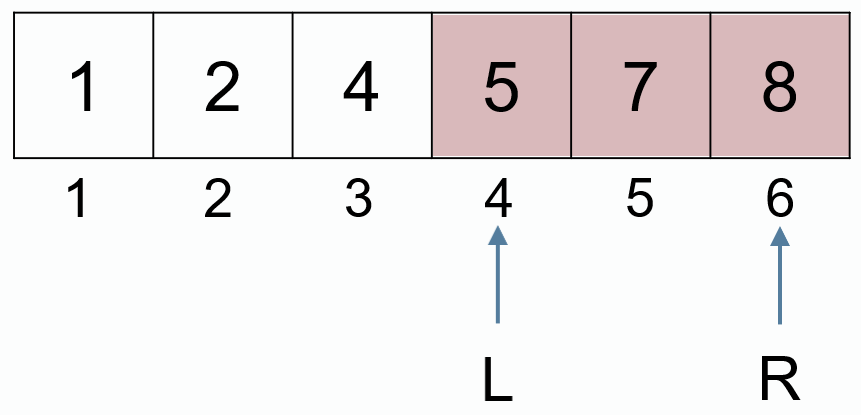
实数域二分查找

// 要求找到的解要保留到小数点后 d-1 位
double L = x1, R = x2, m;
while(R - L >= 1e-d) { //数字d要直接写出来
   m = (L + R) / 2;
   if(要找的解大于m)
      L = m;
   else
      R = m;
}

二分答案

使用场景：要求我们求出某变量在满足某种条件下的最大值或最小值。

使用前提:

答案在一个固定的区间内
难以通过搜索来找到符合要求的值，但给定一个值你可以很快的判断它是不是符合要求
可行解对于区间要符合单调性

求满足某条件的最小值

// check()函数：判断某答案是否满足条件

while(L < R) {
    int mid = (L + R) / 2;
    if(check(mid)) //如果满足条件，看左半部分
        R = mid;
    else
        L = mid + 1;
}

求满足某条件的最大值

while(L < R) {
    int mid = (L + R + 1) / 2;
    if(check(mid)) //如果满足某一条件，看右半部分
        L = mid;
    else
        R = mid - 1;
}

快速排序

每一轮挑选一个基准元素（随机选择，编程时一般选取第一个），并让比它大或小的元素移动到基准元素的两边，把数列拆解成了两个部分。而后对这两部分分别进行快速排序。

时间复杂度：O(nlogn)，辅助空间复杂度：O(logn)，不稳定

最坏时间复杂度： $O(n^2)$

例如，从小大到排序，找一个基准值为 5。

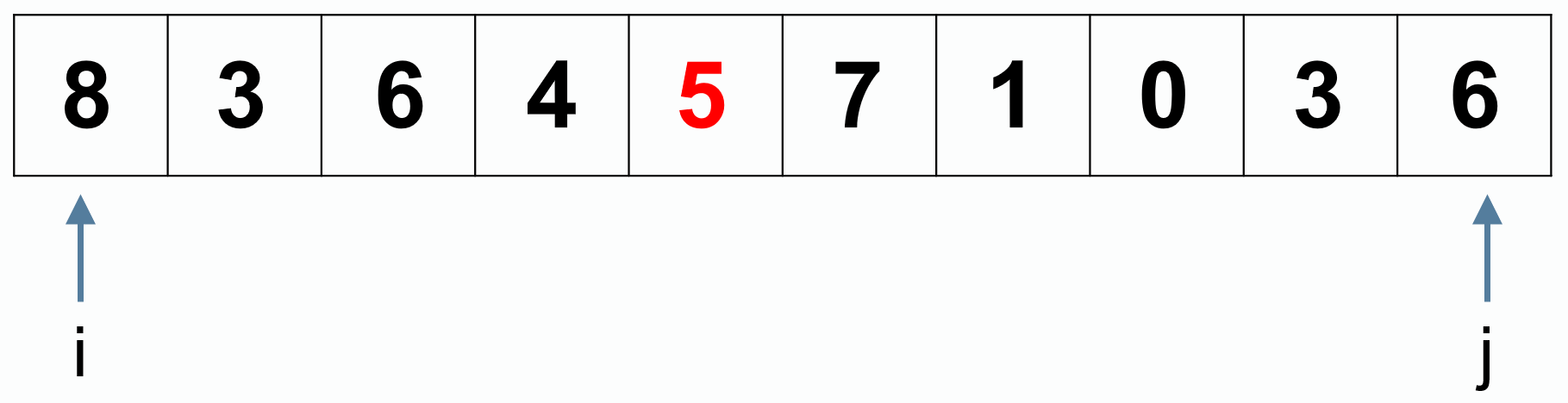
左侧 8 是第一个比 5 大的数字，右侧 3 是第一个比 5 小的数字。

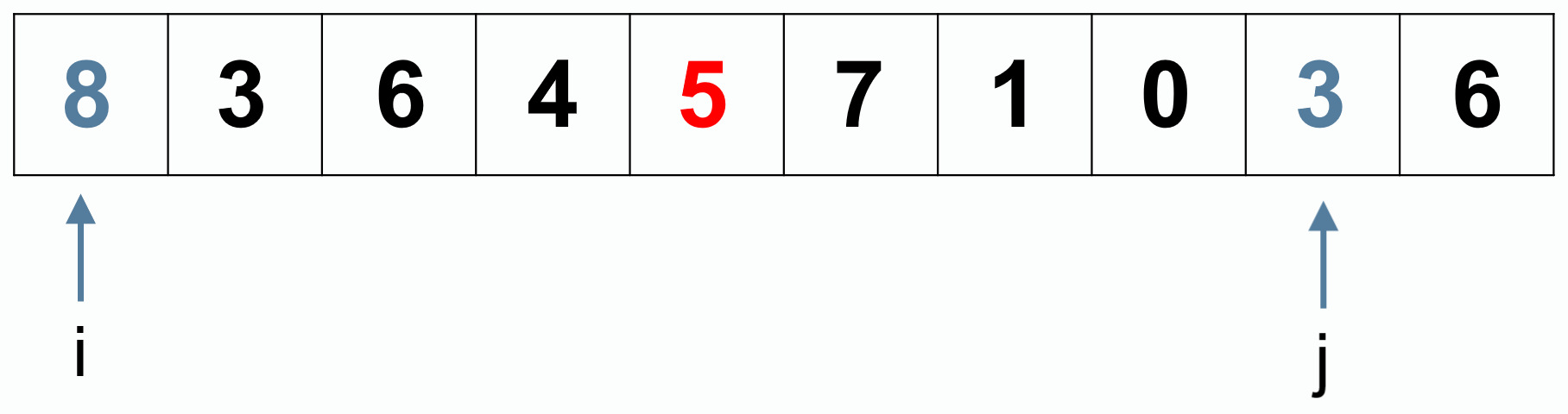
交换 8 和 5：

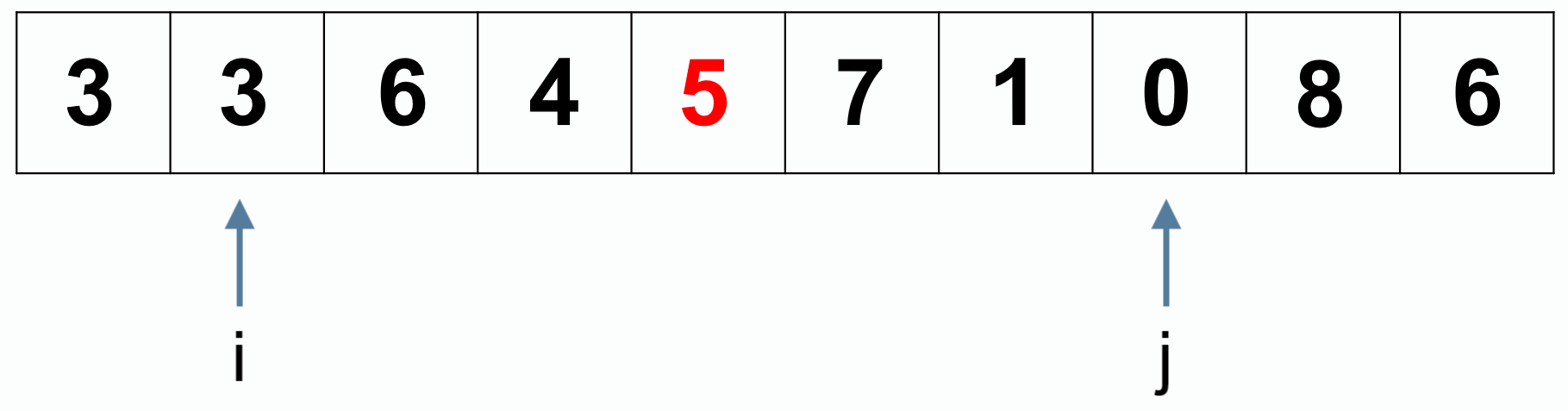
最后分为比 5 小的一组和比 5 大的一组，然后继续分治：

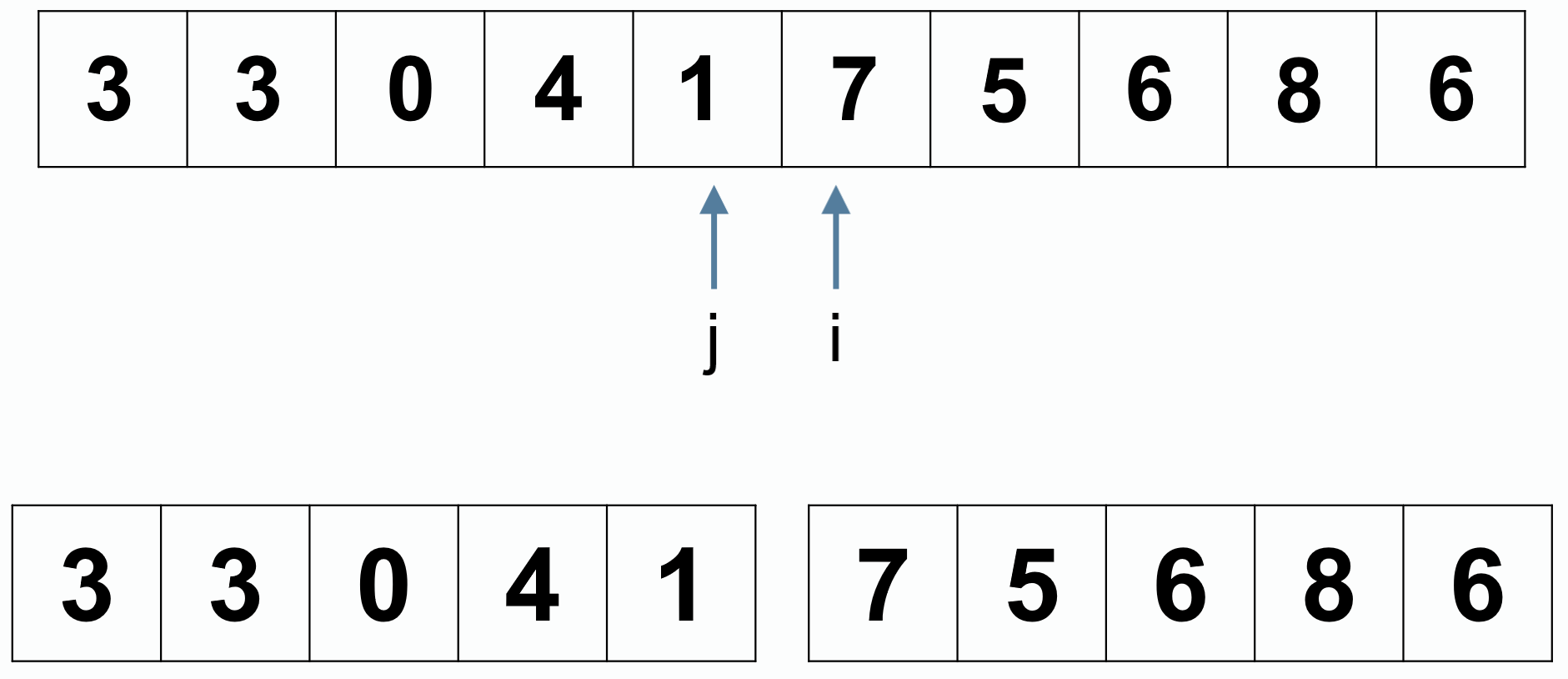
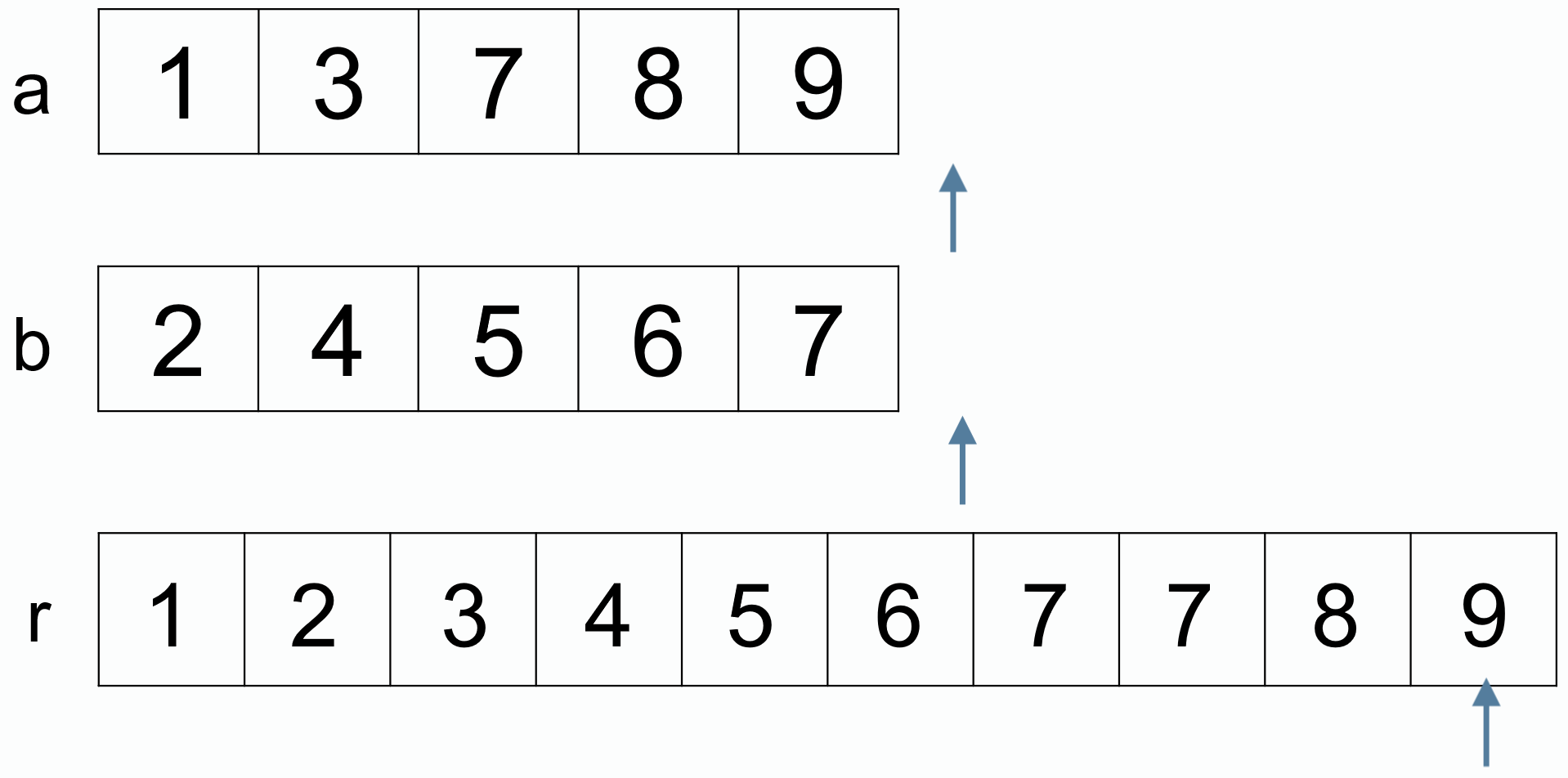
归并排序

对序列的元素进行逐层折半分组，然后从最小分组开始比较排序，逐层进行合并。

时间复杂度：O(nlogn)，辅助空间复杂度：O(n)，稳定。

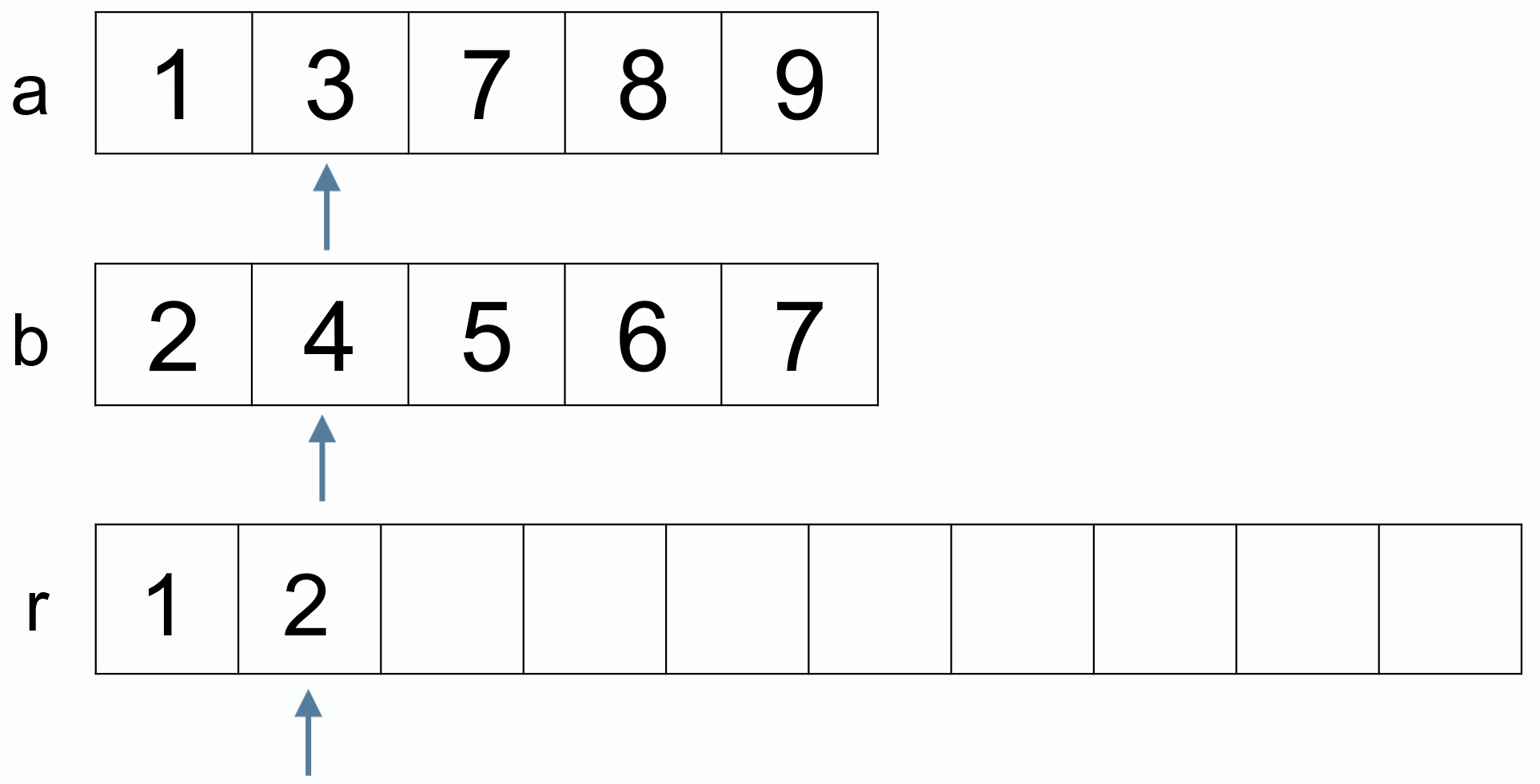
依次类推：

分治算法时间复杂度：

$f(n)=2f(\frac{n}{2})+n$

$=2^2f(\frac{n}{2^2})+2n$

$=2^kf(\frac{n}{2^k})+kn$

令 $n=2^k$ ，则 $k=log_2n$

推导出： $nf(1)+log_2n\times{n}$

时间复杂度为： $O(nlogn)$

归并排序常考应用：求逆序对 res = mid - i + 1

04-分治算法

找伪币