枚举算法

枚举算法也叫穷举法、暴力破解法。是考试竞赛、项目开发中，最常用的方法。

1.将问题的所有可能的答案一一列举出来。

2.根据条件判断此答案是否合适。

3.合适就保留，不合适就舍弃。

但是对于计算机来说，枚举法是利用s计算机运算速度快、精确度高的特点，对要解决问题的所有可能情况，一个不漏地进行检验，从中找出符合要求的答案。

比如，黑猫老师要了解一下哪些同学没有完成作业？逐个检查班级中所有同学的作业情况。枚举每一行，每一列的每一位同学。

当然，现在黑猫老师有【黑猫OJ】可以直接一目了然采集学员作业信息。

模拟算法

模拟算法：根据题目给出的规则对题目要求的相关过程进行编程模拟。

解题步骤：

仔细读题，记录关键信息，反复核对。
分析有哪些关键要素，将关键要素抽象为程序变量与结构。
逐步细化实现题目中描述的过程。
测试输入样例，如果有必要还需自己构造更多样例。

什么是散列表？

散列表，也称哈希表，是一种高效的数据结构。最大优点就是把数据存储和查找所消耗的时间大大降低，几乎可以看成是 O(1) 的，而代价是消耗比较多的内存。因此，空间换时间是散列表的主要特点。

以「key-value」形式存储数据的数据结构：指任意的键值 key 都唯一对应到内存中的某个位置。只需要输入查找的键值，就可以快速地找到其对应的 value。
散列表最常见的应用是将字符或者字符串类型映射为数组下标。
然而，我们可以把散列表理解为一种“高级的数组”，但是这种特殊的“高级数组”的下标可以是很大的整数，浮点数，字符串甚至结构体，而不一定是整数类型。

散列函数

要让键值对应到内存中的位置，就要为键值计算索引，也就是计算这个数据应该放到哪里。根据键值计算索引的函数就叫做散列函数，也称哈希函数。

举个例子，如果键值是一个人的身份证号码，哈希函数就可以是号码的后四位，生活中常用的「手机尾号」也可以当做一种哈希函数。在CSP 初赛中主要考察的就是哈希函数和哈希冲突。

我们可以通过散列函数把数据值对应到一个数组下标，以加快查找的速度。（常用手段）

例：输入一串小写字母，请分别输出其中 a,b,...,z 各个字母出现的次数。

例：用散列表存储以下线性表 18，75，60，43，54，90，46

假设选取的散列函数为 h(K) = K mod M，K 为元素的关键字，M 为散列表的长度，用余数作为存储该元素的散列地址。K 和 M 均为正整数，并且 M 要大于或等于线性表的长度 n。此例 n = 7，故取 M = 13 就已经足够，得到的每个元素的散列地址为：

h(18)=18 mod 13 = 5
h(75)=75 mod 13 = 10
h(60)=60 mod 13 = 8
h(43)=43 mod 13 = 4
h(54)=54 mod 13 = 1
h(90)=90 mod 13 = 12
h(46)=46 mod 13 = 7

该例数据存储时没有发生冲突。

哈希冲突

当两个不同的数经过哈希函数计算后得到了同一个结果，即他们会被映射到哈希表的同一个位置时，即称为发生了哈希冲突。简单来说就是哈希函数算出来的地址被其它元素占用了。

合理选择哈希函数可以减少冲突概率，扩大哈希表范围也可以减少冲突概率，但是不能够避免冲突。

开放地址

遇到冲突时，寻找新的空闲地址。主要包括线性探测法和平方探测法。

1：线性探测法： 当我们所需要存放值的位置被占了，我们就往后面加i并对 M 取模，直至存在一个空余的地址供我们存放值。

公式：h(x) = (Hash(x) + i) mod (Hashtable.length); // i逐渐加1

例：给定 6 个值：0、1、2、6、7、8，设哈希表容量 M 为 6。

0、1、2 可以直接存储，不存在哈希冲突。

根据公式：h(6) = (6+0) % 6 = 0

由于 0 位置已经被占用，i +1 进行第 2 次运算 h(6) = (6+1) % 6 = 1

由于 1 位置已经被占用，继续 i +1 进行第 3 次运算 h(6) = (6+2) % 6 = 2

由于 2 位置已经被占用，继续 i +1 进行第 4 次运算 h(6) = (6+3) % 6 = 3

因为 3 位置未被占用，所以 6 最终存在 3 位置。

其余数字同理计算。

存在问题：出现非同义词冲突（两个不相同的哈希值，抢占同一个后续的哈希地址）被称为堆积或聚集现象。

2：平方探测法(二次探测)

当我们需要存放值的位置被占了，会前后寻找而不是单独方向的寻找。

公式：h(x)=(Hash(x) +i) mod (Hashtable.length); // i 依次为 + $i^2$ 和 - $i^2$

例：给定 3 个值：0、1、5，设哈希表容量 M 为 5。

0、1可以直接存储，不存在哈希冲突。

根据公式：h(5) = (5+ $0^2$ ) % 5 = 0

由于 0 位置已经被占用，i +1 进行第 2 次运算 h(5) = (5+ $1^2$ ) % 5 = 1

由于 1 位置已经被占用，继续 i +1 进行第 3 次运算 h(5) = (5- $1^2$ ) % 5 = 4

因为 4 位置未被占用，所以 5 最终存在 4 位置。

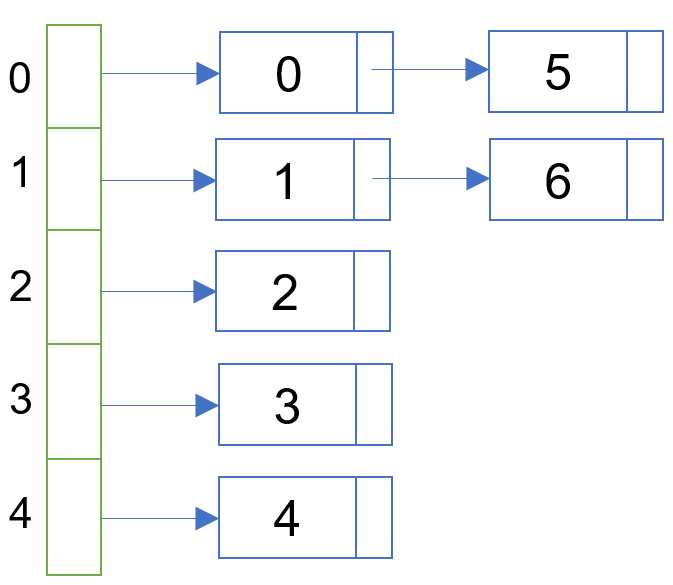
链接地址法

例：给定 6 个值：0、1、2、3、4、5、6，设哈希表容量 M 为 5。

0、1、2、3、4可以直接存储，不存在哈希冲突。

根据公式：

h(5) = 5 % 5 = 0，发生冲突，链接在 0 后面

h(6) = 6 % 5 = 1，发生冲突，链接在 1 后面

将所有哈希地址相同的记录都链接在同一链表中。

公式：h(x)=x mod (Hashtable.length);

再哈希法

同时构造多个不同的哈希函数，等发生冲突时就使用第 2 个、第 3 个......等其他的哈希函数计算地址，直至不发生冲突为止。虽然不易发生聚集，但是增加了计算时间。

建立公共溢出区

将哈希表分为基本表和溢出表，将发生冲突的都存放在溢出表中。

STL set

集合是 C ++ STL（标准模板库）的一部分。其中每个键都是唯一的，可以插入或删除但不能更改。

头文件： #include <set>

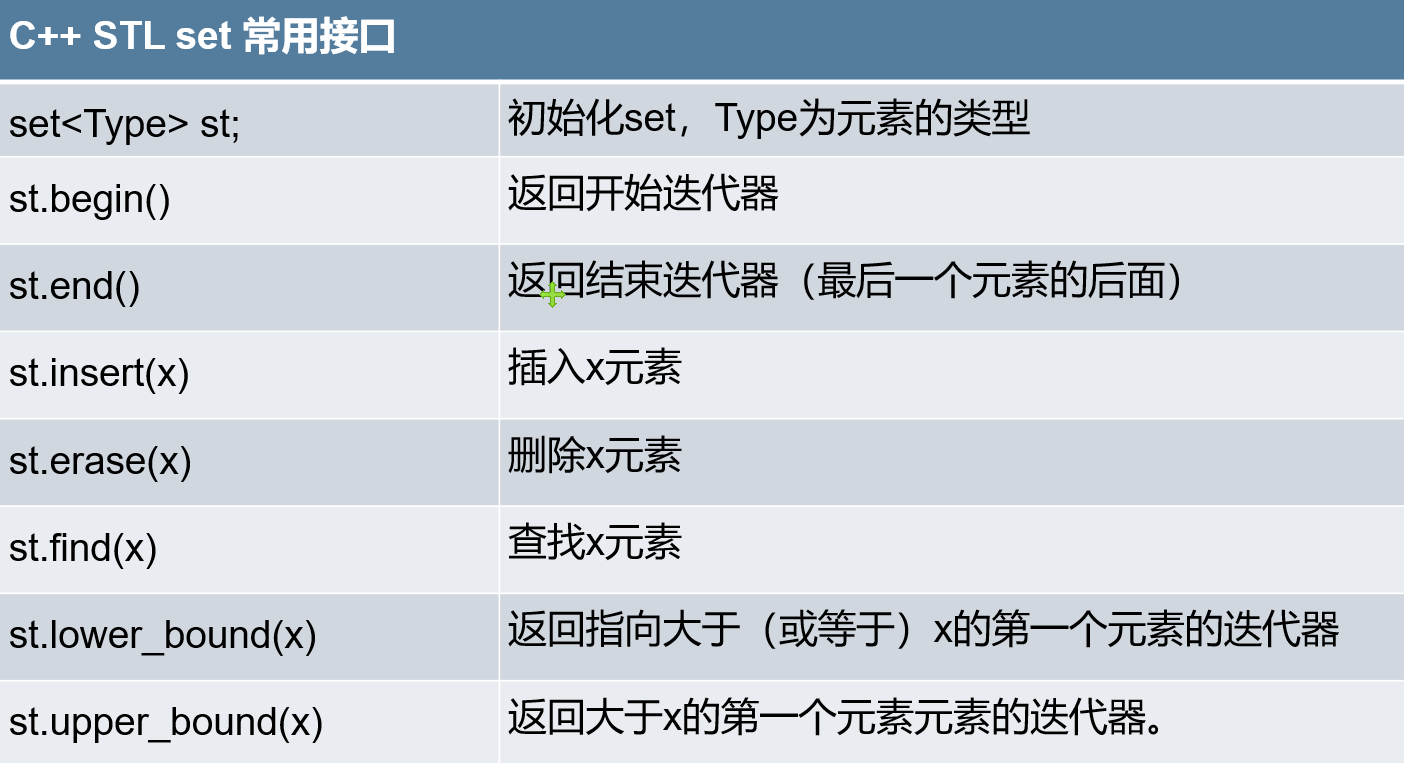
set 基于红黑树实现，插入、删除、查找元素时间复杂度均为 O(logn)，元素有序。

unordered_set 基于哈希实现，插入、删除、查找元素时间复杂度均为 O(1)，元素无序。

#include <bits/stdc++.h>
using namespace std;

int main() {

    set<int> st;

    for(int i = 1; i <= 6; i++){
        st.insert(i);
        st.insert(i + 1);
    }

    st.insert(8);
    st.erase(3);
    for(int x: st) cout << x << ' ';
    cout << endl;

    return 0;
}

STL map

map 是记录 <关键字，数值> 形式元素的容器。可以认为保存的元素按关键字次序构成一棵红黑树，插入，删除，查找一个元素的时间复杂度是 O(logn) 级的。

头文件： #include<map>

定义方法：map<typename1，typename2> mp;

unordered_map 基于哈希实现，插入，删除，查找一个元素的时间复杂度是 O(1) 级的，关键字无序。

补充：万能头文件

经过《CSP-J 闯关系列课程-黑猫一站通C++语法》的学习，我们已经可以灵活运用 C++ 语言，且掌握了很多头文件，在之后的算法课程中我们将继续学习更多头文件。

然而如果头文件记不住，我们就不能使用对应的函数，那该怎么办？

#include <bits/stdc++.h>：几乎包含所有的可用到的 C/C++ 库函数，因此我们也称之为万能头文件。（黑猫OJ 支持万能头文件）

缺点：

1.不属于 GNU C++ 库的标准头文件，在某些情况可能会编译失败。

2.包含了很多不需要的头文件，增加了编译时间。

3.使用万能头会导致部分标识符被占用而无法作为全局变量使用。

4.仅适用于在线OJ比赛使用，不适用工程开发。

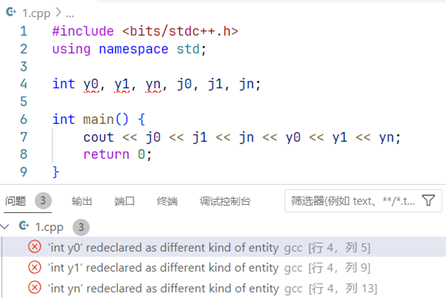
代码报错是因为万能头文件下包含了 math.h

math.h 下面包含的 mathcalls.h 中有对 j0,j1,jn,y0,y1,yn 的定义

所以才报错 重定义 噢！

优点：

1.在竞赛中节约时间。

2.减少了编写头文件的工作量。

万能头文件包含大量不需要的库的头文件，更适合在在线 OJ 比赛中使用，不过在国内 OJ 中，例如 POJ、HDU 不支持这个函数，其他国外的 OJ，还有台湾的 OJ 都支持，CF，Topcoder也都支持。然而，在具体的软件工程的开发中，应该减少包含，控制编译时间和代码大小。

01-枚举、模拟和散列表