什么是贪心算法？

算法思想：

遵循某种规律，不断选取当前最优策略的算法设计方法（不从整体考虑，仅“目光短浅”的考虑当前的局部最优解）。贪心没有固定的算法框架，算法设计的关键是贪心策略的选择。

多阶段决策过程: 问题可以按时间顺序分解成若干相互联系的阶段，在每一个阶段都要做出决策，全部过程的决策是一个策略。

最优子结构和无后效性

**最优子结构指的是，问题的最优解包含子问题的最优解。**

反过来说：我们可以通过求解子问题的最优解，推导出问题的最优解。

无后效性，有两层含义：

在推导后面阶段状态的时候，我们只关心当前阶段的状态值，不关心这个状态是怎么一步步推导出来的。
**某阶段状态一旦确定，就不受之后阶段的决策影响。**

贪心问题解题过程

建立数学模型
确定最优子结构

如何将要求解的大问题分解成子问题
思考贪心策略选择的条件

应该选择满足什么条件的元素加入解
证明贪心选择性质

活动安排问题解题过程

建立数学模型：线段覆盖
确定最优子结构

选择一个活动后，在n-1个活动中选择最多的不重叠的活动
思考贪心策略选择的条件

选择：不与已选择活动重叠的，结束时间最早的活动
证明贪心选择性质

证明贪心选择性质

要想证明贪心选择能否得到最优解，只需要证明最优解包含每一次的贪心选择。

使用数学归纳法：

是否存在最优解包含第一次的贪心选择
假设存在最优解包含前k次的贪心选择，该最优解是否包含第k+1次的贪心选择

证明：存在最优解包含第一次的贪心选择

使用反证法

假设所有最优解都不包含第一次的贪心选择
对于某一最优解，如果第一次采用贪心选择，也仍然能得到最优解。这与假设相悖。
原命题得证。

证明：在k次贪心选择后，存在最优的活动选择方案包含第k+1次的贪心选择：不与前面重叠的结束时间最早的活动 $A_g$ 。

假设所有最优解都不包含活动 $A_g$
对于某一最优解，活动序列按结束时间排序为： $A_1,A_2,...,A_k,A_{k+1},...,A_n$ ，如果将 $A_g$ 替换 $A_{k+1}$ ，仍然能形成最优解，这与假设相悖。
原命题得证。

动态规划概念

动态规划（Dynamic Programming），简称DP。是求解最优化问题的一种常见策略。

和分治法一样，动态规划也是把一个复杂问题分解成相对简单的“子问题”的方式求解，再组合出答案的方法。不过，分治法是将问题划分成一些“独立”的子问题，递归地求解各子问题，然后再合并子问题的解而得到原问题的解，如二分查找、快速排序等问题。与此不同，动态规划适用于子问题不是独立的情况，也就是子问题包含公共的“子子问题”。

**动态规划算法对每个子子问题只求解一次，并且立刻将其结果保存到一张“表”中，从而避免后面每次遇到子子问题时重复去计算。**

背包问题

给定一组物品，每种物品都有自己的重量和价值，在限定的总重量内，我们如何选择，才能使得物品的总价值最高。

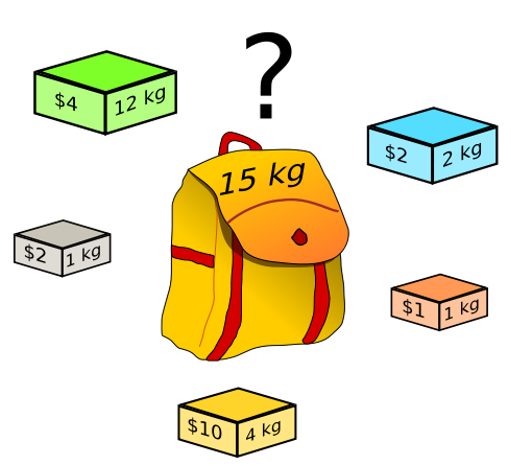
网格解题法：

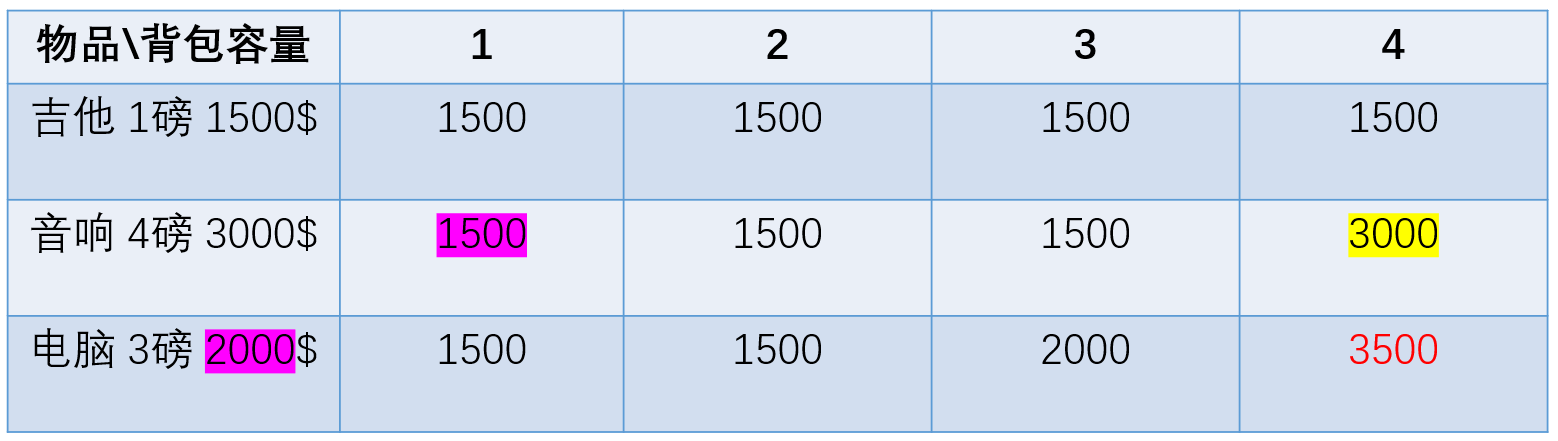
对于每一种物品，都有选和不选两种决策。

选第 i 种商品： $f[i][j] = v + f[i-1][j-w]$ 。

不选第 i 种商品： $f[i][j] = f[i-1][j]$ ，如果可以装下，取两者最大值。

01背包问题

一个旅行者有一个最多能装m公斤的背包，现在有 n 件物品，第i件物品的重量是w[i]，价值为c[i]，求旅行者能获得最大总价值。

特点：每种物品仅有一件，可以选择放或不放。

核心代码：

for(int i = 1; i <= n; i++){
    int w, c;
    cin >> w >> c;
    for(int j = 1; j <= m; j++){
        if(j >= w)
            f[i][j] = max(f[i - 1][j], c + f[i - 1][j - w]);
        else
            f[i][j] = f[i - 1][j];
    }
}

降维优化：

for(int i = 1; i <= n; i++){
    int w, c;
    cin >> w >> c;
    for(int j = m; j >= w; j--){
        f[j] = max(f[j], c + f[j - w]);
    }
}

滚动数组优化：

for(int i = 1; i <= n; i++){
    int w, c;
    cin >> w >> c;
    for(int j = 1; j <= m; j++){
        if(j >= w)
            f[i & 1][j] = max(f[(i - 1) & 1][j], c + f[(i - 1) & 1][j - w]);
        else
            f[i & 1][j] = f[(i - 1) & 1][j];
    }
}

完全背包问题

有一个最大载重m的背包，有 n 种物品，第i种物品的重量是w[i]，价值为c[i]，每种物品都有无限件可用。从n种物品中选取若干件，使其重量的和小于等于m，且价值的和为最大。

特点：每种物品最多可以取无限件。

核心代码：

for(int i = 1; i <= n; i++){
    int w, c;
    cin >> w >> c;
    for(int j = 1; j <= m; j++){
        if(j >= w)
            f[i][j] = max(f[i - 1][j], c + f[i][j - w]);
        else
            f[i][j] = f[ i - 1][j];
    }
}

降维优化：

for(int i = 1; i <= n; i++){    
    int w, c;
    cin >> w >> c;
    for(int j = w; j <= m; j++)
        f[j] = max(f[j], c + f[j - w]);

}

滚动数组优化：

for(int i = 1; i <= n; i++){
    int w, c;
    cin >> w >> c;
    for(int j = 1; j <= m; j++){
        if(j >= w)
            f[i & 1][j] = max(f[(i - 1) & 1][j], c + f[i & 1][j - w]);
        else
            f[i & 1][j] = f[(i - 1) & 1][j];
    }
}

最长上升子序列（LIS）问题

一个数的序列 $b_i$ ，当 $b_1<b_2<...<b_S$ 的时候，我们称这个序列是上升的。

最长上升子序列(LIS：Longest Increasing Subsequence）

求某序列的最长上升子序列的长度。

例如：

原序列：1 7 3 5 9 4 8

最长上升子序列：1 3 4 8 长度：4

状态定义：f[i] 以第i元素为结尾的最长上升子序列的长度。

14-贪心和DP