什么是搜索算法？

人类：随机选取通向出口方向的路，想去哪儿就去哪儿（不稳定，也许能够一下子找到出口，也许需要很长时间才能够找到出口）。

计算机：按照固定规则来选取方向并前进（稳定，在一定时间内一定能找到出口）。

解空间：所有可能得到的解的集合。

解空间树：由解构成的树状结构。

什么是DFS？

深度优先搜索算法（Depth First Search，DFS) ，简称深搜，或回溯法、试探法。 在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发探索解空间树。从一条路走到底，能进则进，不能进则退。

对于每一个能用DFS解决的问题都有一棵答案树。

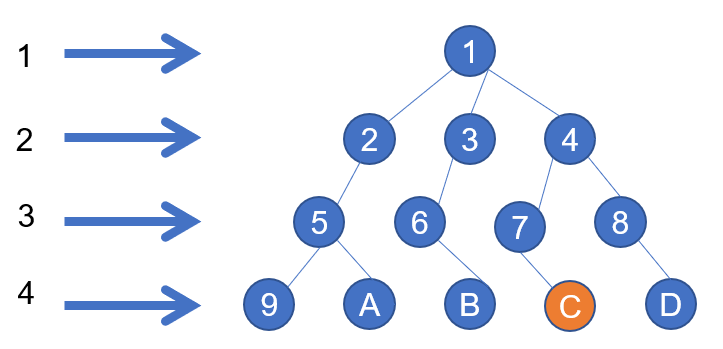
假设这是某个题目的答案树且 C 为题目的答案，那么我们需要从 1 走到 C，这对于人类来说是直观的，可对于计算机并不如此，计算机需要一次一次的尝试，每次尝试在答案树中的体现就是向下进一个层级。

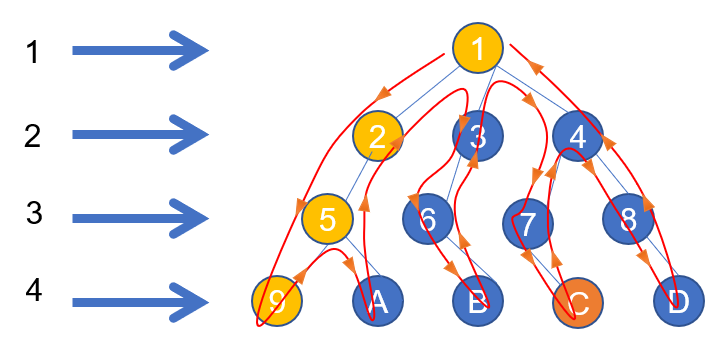
因此计算机想要走到C的话需要1➡2➡5➡9➡A➡3➡6➡B➡4➡7➡C这样的路线 先从1沿着️黄色的路线一直走到9，发现没法再往下走，就回头寻找别的出路... 因此：不撞南墙不回头。

深搜常用模板

void dfs(搜索层数) {
    if (找到解) {
        输出解;
        return;
    }
    if (不满足条件)
        return;
    for (i = 1; i <= 下一层情况数; i++) {
        更新状态
　　　   dfs(搜索层数 + 1);
        恢复状态
    }
}

全排列问题

输出自然数 1 到 n 所有不重复的排列，即 n 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

#include <iostream>  
#include <cstdio>
using namespace std; 

const int N = 15;

int n;
int path[N];    // 存储数字的盒子
bool book[N];  // 标记数组 不能走回头路

// u为当前盒子编号
void dfs(int u){
    // 返回条件
    // 当走到n+1返回
    if(u == n + 1){
        // 一次搜索完成 打印结果
        for(int i = 1; i <= n; i++)
            printf("%3d", path[i]);
        cout << endl;
        return;
    }

    // 枚举手里面所有的数字
    for(int i = 1; i <= n; i++){
        // 数字不能被标记过
        if(!book[i]){
            book[i] = true; // 标记数字i
            path[u] = i;    // 数字i放到盒子u中
            dfs(u + 1);        // 搜索
            book[i] = false;    // 回溯 取消标记
        }
    }
}

int main(){

    cin >> n;

    dfs(1);    // 从第一个格子开始填充


    return 0;
}

组合的输出

排列与组合是常用的数学方法，其中组合就是从n个元素中抽出r个元素(不分顺序且r≤n)，我们可以简单地将n个元素理解为自然数1，2，…，n，从中任取r个数。

现要求你用递归的方法输出所有组合。

例如n＝5，r＝3，所有组合为：

1 2 3

1 2 4

1 2 5

1 3 4

1 3 5

1 4 5

2 3 4

2 3 5

2 4 5

3 4 5

题目解析：

组合数按照从小到大的顺序输出，意味着当前盒子中要选择的数字至少比上一个盒子中的数字个数大1。

返回条件：当走到第 r + 1 个盒子结束。

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 30;

int n, r;
int a[N];

void dfs(int u){
    if(u > r){
        for(int i = 1; i <= r; i++)
            printf("%3d", a[i]);
        puts("");
          return;
    }

    for(int i = a[u - 1] + 1; i <= n; i++){
        a[u] = i;
        dfs(u + 1);
    }
}

int main() {

    cin >> n >> r;
    dfs(1);

    return 0;
}

指数型枚举

从1∼n这 n（n≤16）个整数中随机选取任意多个，输出所有可能的选择方案。

题目解析：

当前数字先标记、选择下一个数字，然后回溯取消标记，再选择下一个数字。

#include <iostream>  
using namespace std; 

int n;
int book[20];

void dfs(int u){
    if(u > n){
        for(int i = 1; i <= n; i++)
            if(book[i])
                cout << i << " ";

        cout << endl;
        return;
    }

    book[u] = true;
    dfs(u + 1);
    book[u] = false;

    dfs(u + 1);
}

int main(){

    cin >> n;
    dfs(1);

    return 0;
}

走迷宫

一个迷宫由R行C列格子组成，有的格子里有障碍物，不能走；有的格子是空地，可以走。

给定一个迷宫，求从左上角走到右下角最少需要走多少步(数据保证一定能走到)。只能在水平方向或垂直方向走，不能斜着走。

题目解析：

方向偏移

迷宫常用模板