一维前缀和

题目描述

输入一个长度为 n​ 的整数序列。

接下来再输入 m​ 个询问，每个询问输入一对 l,r​。

对于每个询问，输出原序列中从第 l​ 个数到第 ​r 个数的和。

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式

共 m 行，每行输出一个询问的结果。

样例

5 3
2 1 3 6 4
1 2
1 3
2 4

3
6
10

提示

1≤l≤r≤n​,

1≤n,m≤100000,

-1000≤数列中元素的值≤1000。

解析：

暴力做法：对于每次询问，都枚举一遍[L,R]区间的数字求和，最坏情况下，时间复杂度为$O(nm)=10^{12}$。

前缀和优化：首先预处理出原数组的前缀和数组s，[L,R]区间的数字和为s[R]-s[L-1]，时间复杂度为$O(n)$。

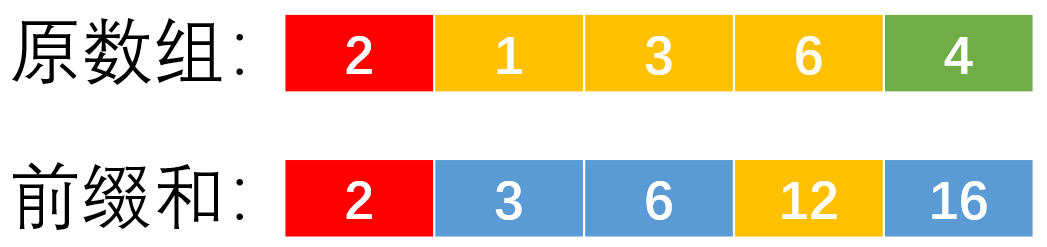
a[2] + a[3] + a[4] = s[4] – s[1] = 12 – 2 = 10

二维前缀和

题目描述

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数n，m，q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含四个整数x1,y1,x2,y2表示一组询问。

输出格式

共q行，每行输出一个询问的结果。

样例

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

17
27
21

提示

数据范围

1≤n,m≤1000, 1≤q≤200000, 1≤x1≤x2≤n, 1≤y1≤y2≤m, −1000≤矩阵内元素的值≤1000。

解析：

暴力做法：对于每次询问，都枚举一遍二维区间的数字求和，最坏情况下，时间复杂度为$O(qnm)=10^{11}$。

前缀和优化：首先预处理出原数组的前缀和数组s，s[i][j]表示从左上角(1,1)开始到右下角(i,j)矩形范围内所有数字之和。

然后每次查询可以在线性时间范围内得出结果，时间复杂度为$O(nm)=10^6$ 。

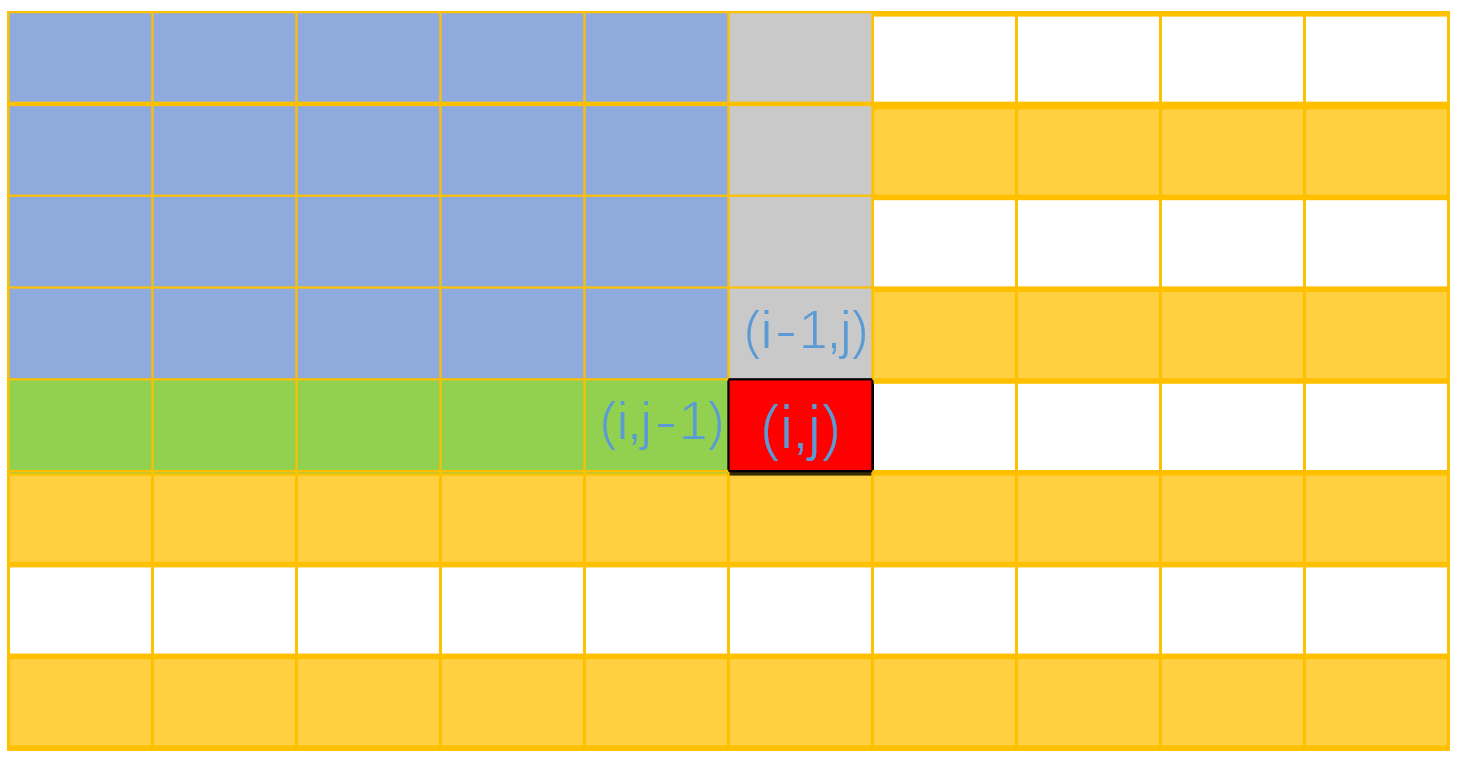
s[i][j] = s[i][j-1] + s[i-1][j] – s[i-1][j-1] + a[i][j]

一维差分

题目描述

输入一个长度为n的整数序列。

接下来输入m个操作，每个操作包含三个整数l,r,c，表示将序列中[l,r]之间的每个数加上c。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数n和m。

第二行包含n个整数，表示整数序列。

接下来m行，每行包含三个整数l，r，c，表示一个操作。

输出格式

共一行，包含n个整数，表示最终序列。

样例

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

3 4 5 3 4 2

提示

数据范围

1≤n,m≤${10^6}$, 1≤l≤r≤n, −1000≤c≤1000, −1000≤整数序列中元素的值≤1000。

解析：

暴力做法：对于每次询问，都枚举一遍[L,R]区间的数字加上c，

最坏情况下，时间复杂度为$O(nm)=10^{12}$。

差分优化：差分是前缀和的逆运算。首先，假定原数组a的差分数组为b，即a[i]=b[1]+b[2]+...+b[i]。

然后a数组在[L,R]区间的数字加上c，就相当于在b数组上进行b[L]+=c，b[R+1]-=c。再将b数组求前缀和的到a数组。时间复杂度$O(n)$。

目标：原数组[3,5]区间数字加上c。

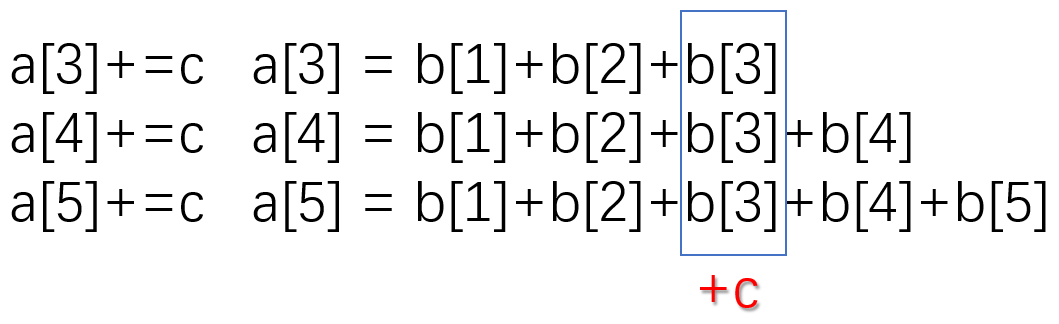
然而，a[6],a[7],a[8]也被迫加上了c，这并不是我们期望的结果。

因此，对b[6]-=c，这样a[6]及其后面的数字就会保持不变。

差分数组b无需特殊构造，在初始状态，a数组和b数组都为0，自然满足b是a的差分数组。

// 在a数组[L,R]区间数字+c
void insert(int L, int R, int c){
    b[L] += c;
    b[R + 1] -= c;
}

初始化时，读入a数组数字，相当于在[i,i]区间插入一个数字c。

for(int i = 1; i <= n; i++) {
    int x;
    cin >> x;
    insert(i, i, x);
}

二维差分

题目描述

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1,y1,x2,y2,c，其中(x1,y1)和(x2,y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数n,m,q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1,y1,x2,y2,c，表示一个操作。

输出格式

共n行，每行m个整数，表示所有操作进行完毕后的最终矩阵。

样例

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

2 3 4 1
4 3 4 1
2 2 2 2

提示

1≤n,m≤1000, 1≤q≤100000, 1≤x1≤x2≤n, 1≤y1≤y2≤m, −1000≤c≤1000, −1000≤矩阵内元素的值≤1000。

解析

暴力做法：对于每次询问，都枚举一遍二维区间的数字+c，

最坏情况下，时间复杂度为$O(qnm)=10^{11}$。

差分优化：首先预处理出原数组的二维差分数组b，a[i][j]表示从左上角(1,1)开始到右下角(i,j)矩形范围内所有b数组数字之和。

然后每次查询可以在线性时间范围内得出结果，时间复杂度为$O(nm)=10^6$。

a数组(x1,y1) → (x2,y2) 区间内数字+c，相当于在差分数组b上进行如下操作。

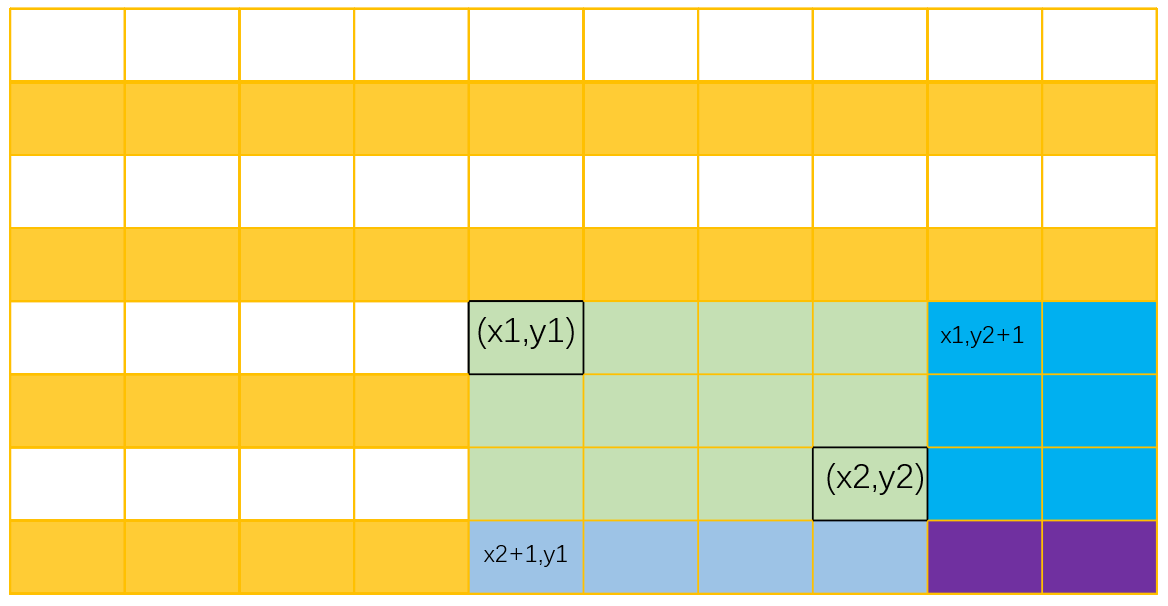
差分数组b无需特殊构造，在初始状态，a数组和b数组都为0，自然满足b是a的差分数组。

void insert(int x1, int y1, int x2, int y2, int c){
    b[x1][y1] += c;
    b[x2+1][y1] -= c;
    b[x1][y2+1] -= c;
    b[x2+1][y2+1] += c;
}

初始化时，读入a数组数字，相当于在区间(i,j)→(i,j)，即这个点插入一个数字c。

for(int i = 1; i <= n; i++){    
    for(int j = 1; j <= m; j++){
        int x;
        scanf("%d", &x);
        insert(i, j, i, j, x);
    }
}