什么是广度优先搜索？

广度优先搜索（又称宽度优先搜索）算法的核心思想是：初始化，生成第一层结点，检查目标结点是否在这些第一层结点中，若没有，再将所有第一层的结点逐一扩展（即其后继结点），得到第二层结点，并逐一检查第二层结点中是否包含目标结点。若没有，再逐一扩展第二层的所有结点……，如此依次扩展，检查下去，直到发现目标结点为止。即：

1. 从图中的某一顶点 $V_0$ 开始，先访问 $V_0$；

2. 访问所有与 $V_0$ 相邻接的顶点 $V_1$，$V_2$，......，$V_t$；

3. 依次访问与 $V_1$，$V_2$，......，$V_t$ 相邻接的所有未曾访问过的顶点；
4. 循此以往，直至所有的顶点都被访问过为止。

这种搜索的次序体现沿层次向横向扩展的趋势，所以称之为广度优先搜索。

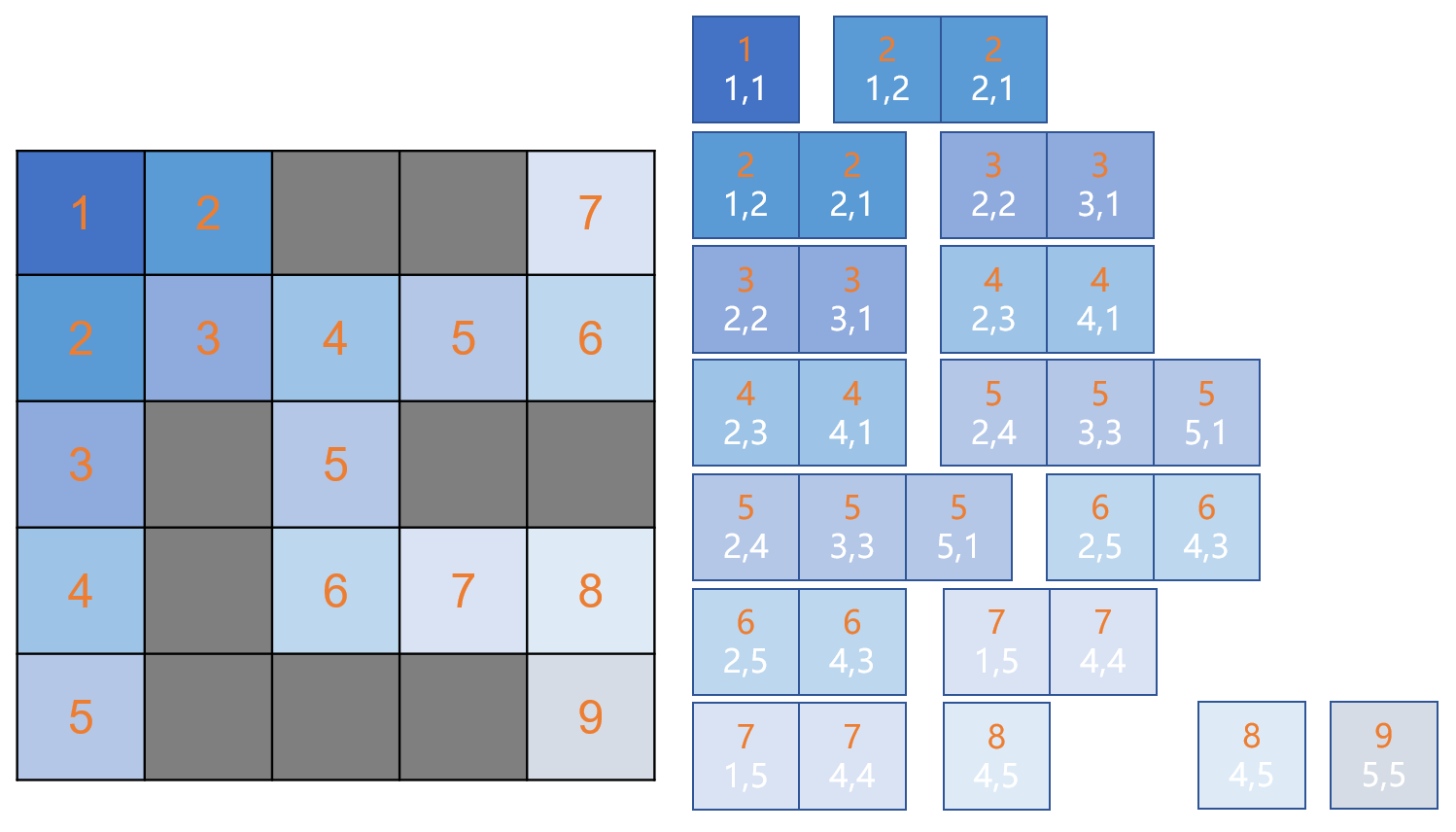
灰色格子表示墙，不可以走；其它颜色格子可以走。

图的广度优先遍历

题目描述

读入一个用邻接矩阵存储的无向图，输出它的广度优先遍历序列。

输入格式

第1行1个正整数n，表示图中顶点数，2≤n≤100；

接下来的n行是一个n×n的邻接矩阵，a[i][j]=1表示顶点i和顶点j之间有直接边相连，a[i][j]=0表示没有直接边相连。保证i=j时，a[i][j]=0，并且a[i][j]=a[j][i]。

输出格式

输出1~n的某一种排列，表示从顶点1开始，对该图进行宽度优先遍历得到的顶点序列，每两个数之间用一个“-”分隔。

样例

8
0 1 1 0 0 0 0 0
1 0 0 1 1 0 0 0
1 0 0 0 0 0 1 1
0 1 0 0 0 1 0 0
0 1 0 0 0 1 0 0
0 0 0 1 1 0 0 0
0 0 1 0 0 0 0 1
0 0 1 0 0 0 1 0

1-2-3-4-5-7-8-6

提示

参考程序：数组模拟队列

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 105;

int n;
int g[N][N];
int q[N];

bool book[N];

bool is_first = true;
void bfs(){
    int hh = 0, tt = -1;
    q[++tt] = 1;
    book[1] = true;

    while(hh <= tt){
        int t = q[hh++];

        if(is_first){
            cout << t;
            is_first = false;
        }
        else
            cout << "-" << t;

        for(int i = 1; i <= n; i++){
            if(g[t][i] && !book[i]){
                q[++tt] = i;
                book[i] = true;
            }
        }
    }
}

int main() {

    cin >> n;

    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            cin >> g[i][j];

    bfs();

    return 0;
}