Dijkstra算法
Dijkstra 算法:采用贪心策略,可以解决单源最短路径问题。
适用要求:图中不存在负权边。
算法可以简单概括为 Dijkstra = BFS + 贪心
算法步骤
设置初始状态:
- S 只包含源点,U 包含除源点外的其他顶点
- U 中顶点v的距离为:若 v 与 s 邻接,距离为 s 到 v 的弧的权值,否则为 INF
从 U 中选出距离 s 最近的顶点 u,并将顶点 u 加入到 S 中;同时,从 U 中移除顶点 u。
更新 U 中各个顶点到源点s的距离。(松弛操作)
重复步骤 2 和 3,直到遍历完所有顶点。
松弛操作
dis[i] 为起点 s 到 i 的最短距离。
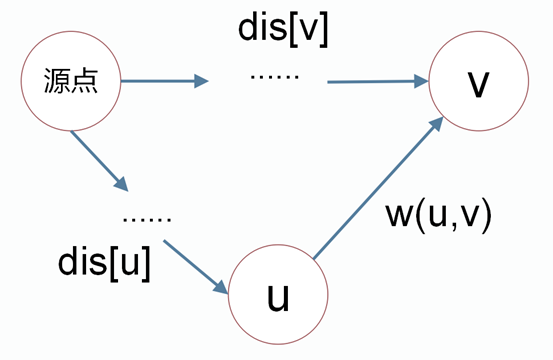
if (dis[v] > dis[u] + w(u,v))
dis[v] = dis[u] + w(u,v)
算法图解
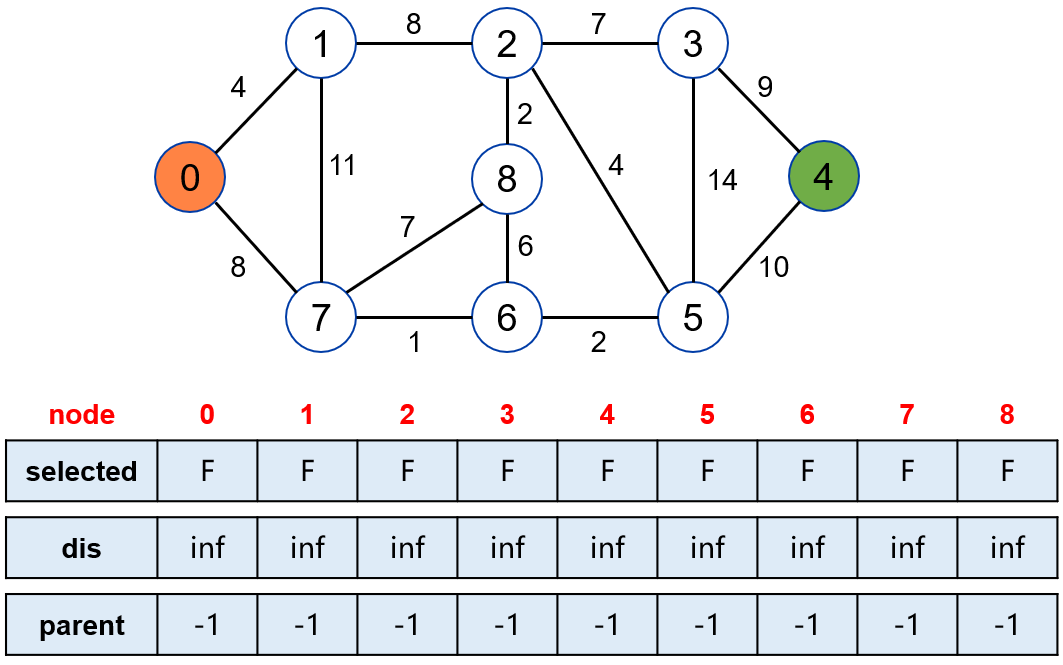
起点 0,终点 4
selected 为已被标记的点
- dis[i] 为从起点到达 i 的最短距离,初始值都是无穷大
- parent[i] 为结点 i 的父节点
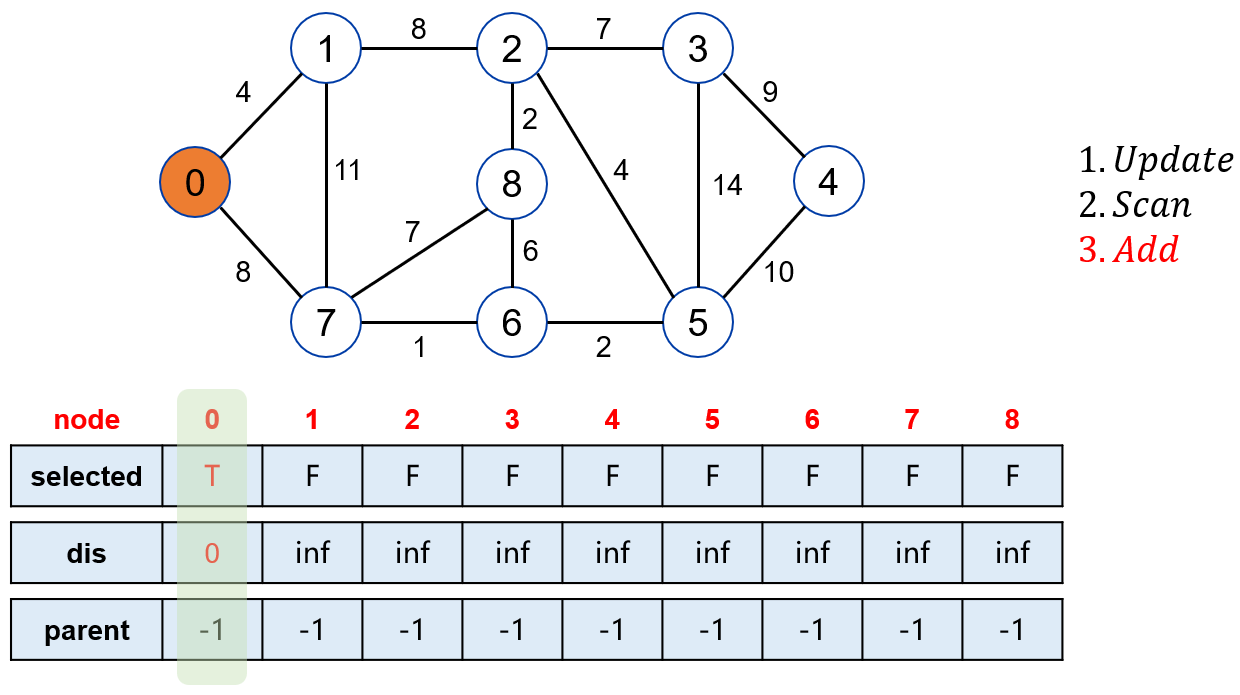
初始化,将起点加入到被标记的集合中,起点距离自身的距离为 0。
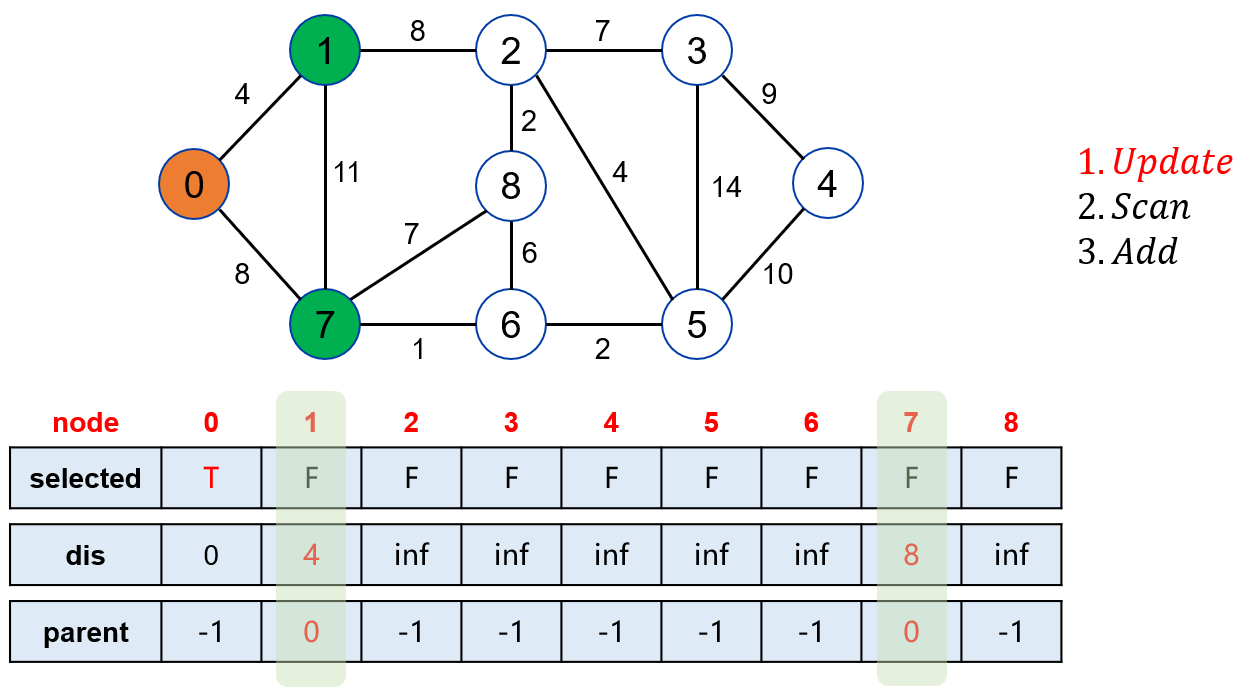
当 0 号点被选中,可以松弛其邻接点 1 和 7。
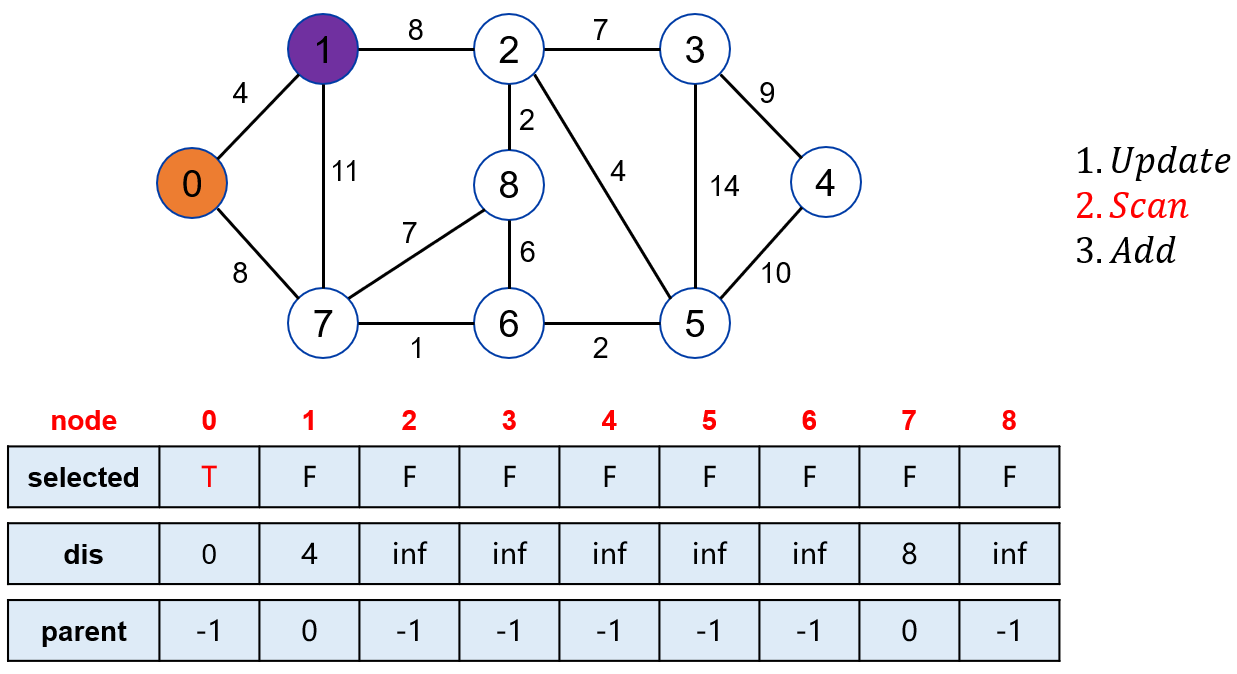
在未被标记的点中,找到距离起点最近的点是 1。
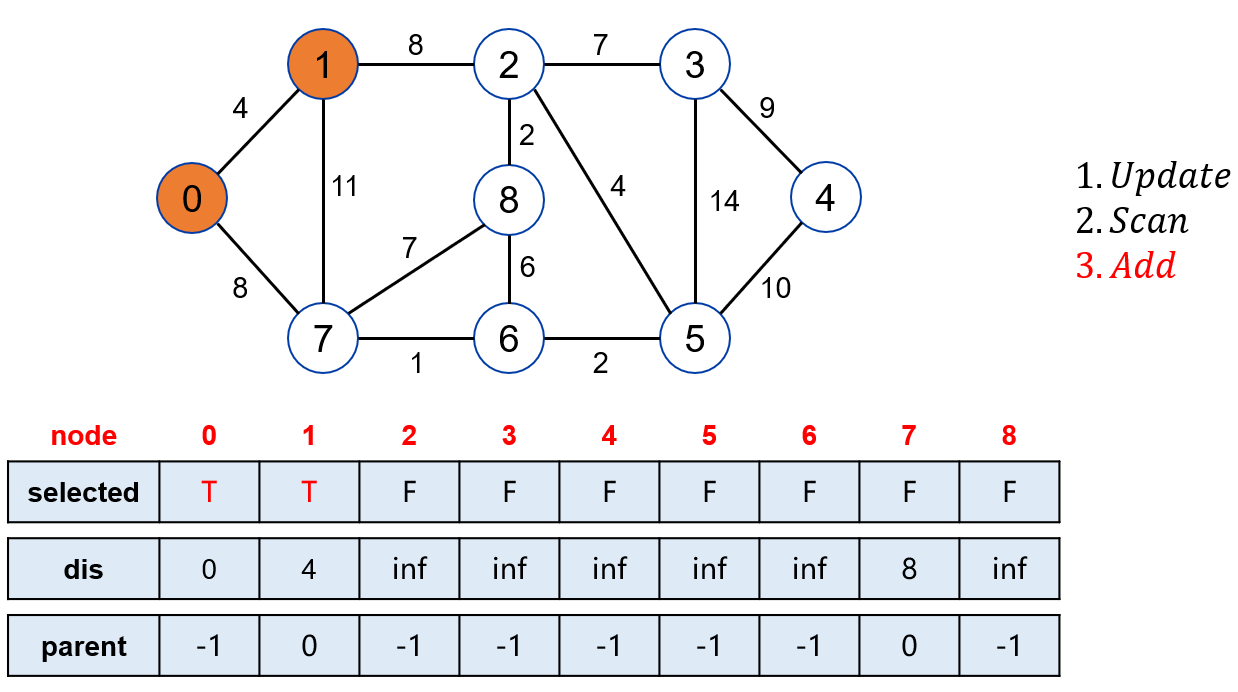
将点 1 标记。
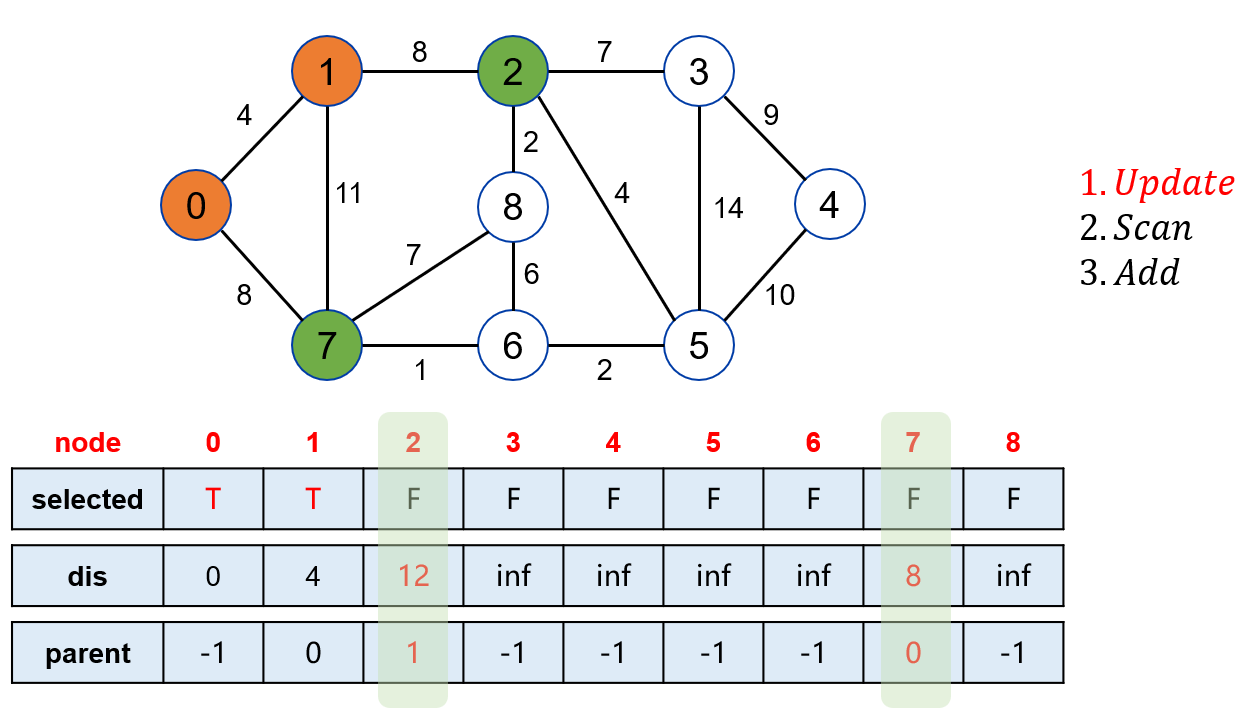
点 1 可以松弛操作点 2 和点 7。
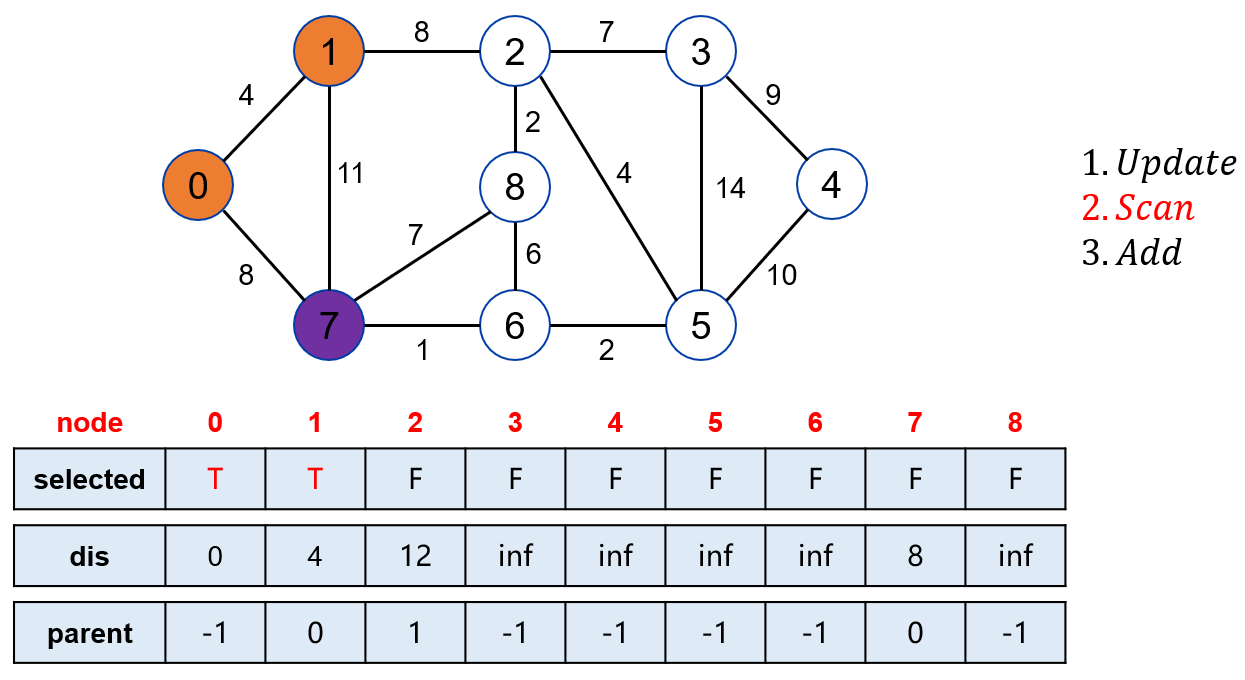
在未被标记的点中,找到距离起点最近的点是 7。
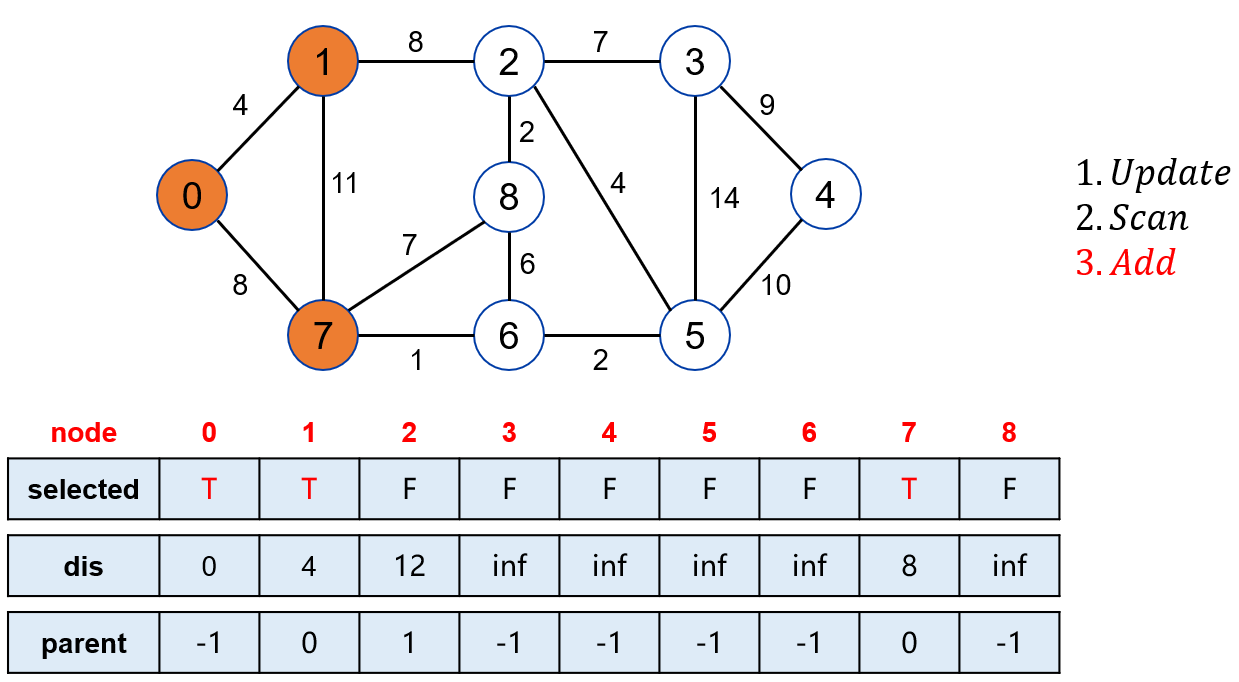
将点 7 标记。
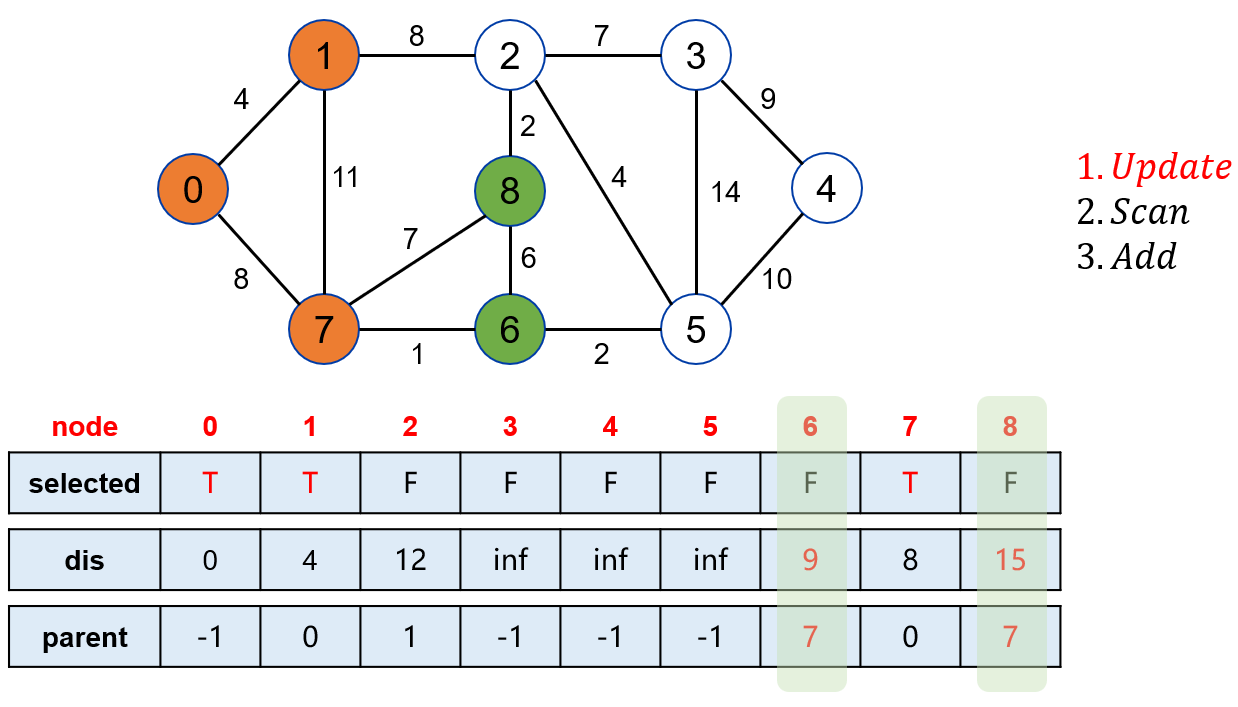
点 1 可以松弛操作点 6 和点 8。
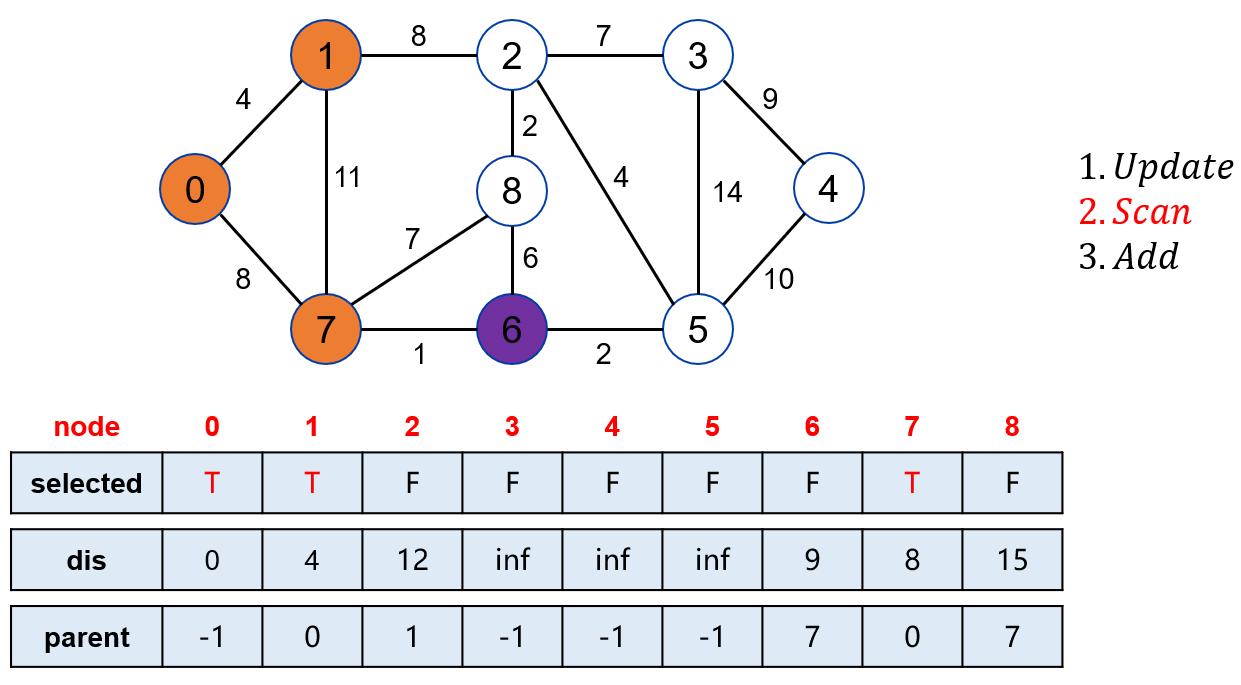
在未被标记的点中,找到距离起点最近的点是 6。
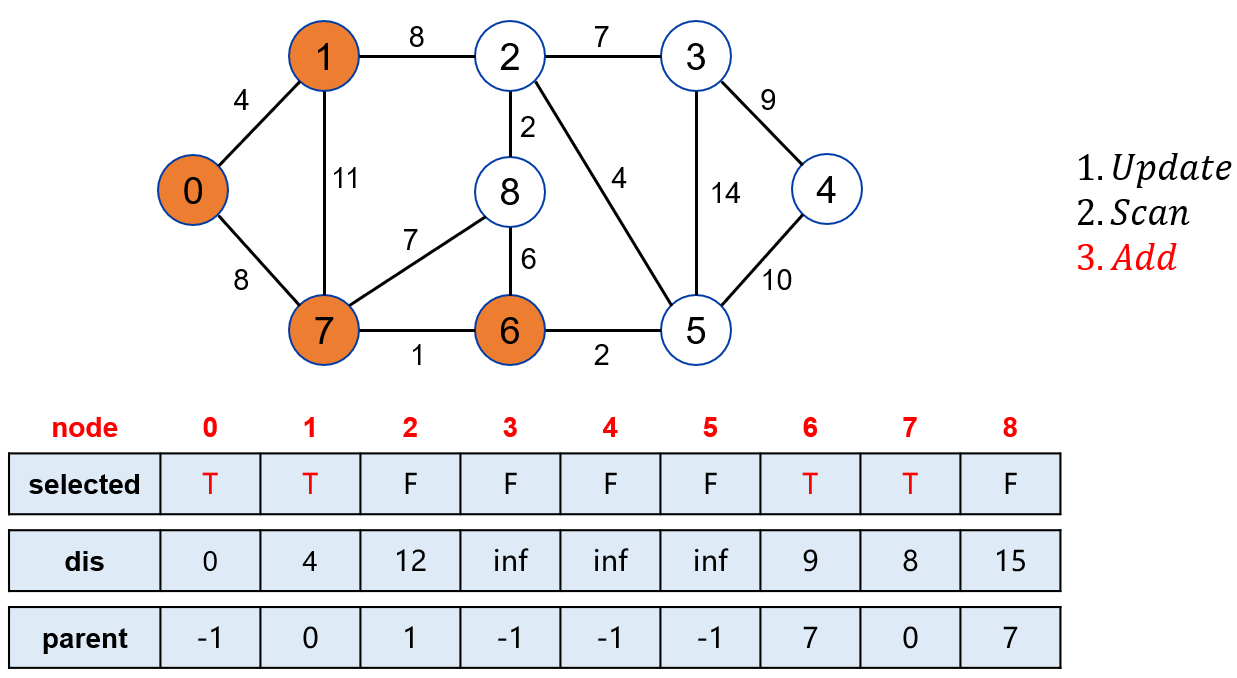
将点 6 标记。
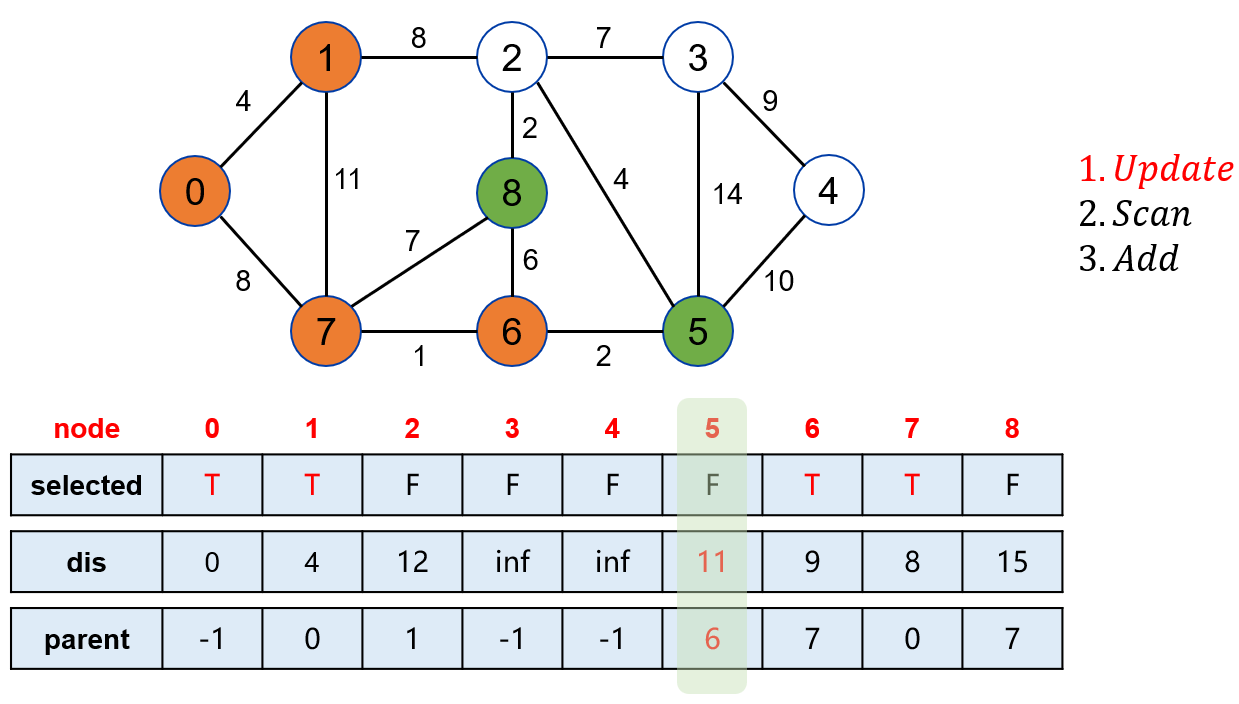
点 1 可以松弛操作点 5 和点 8。
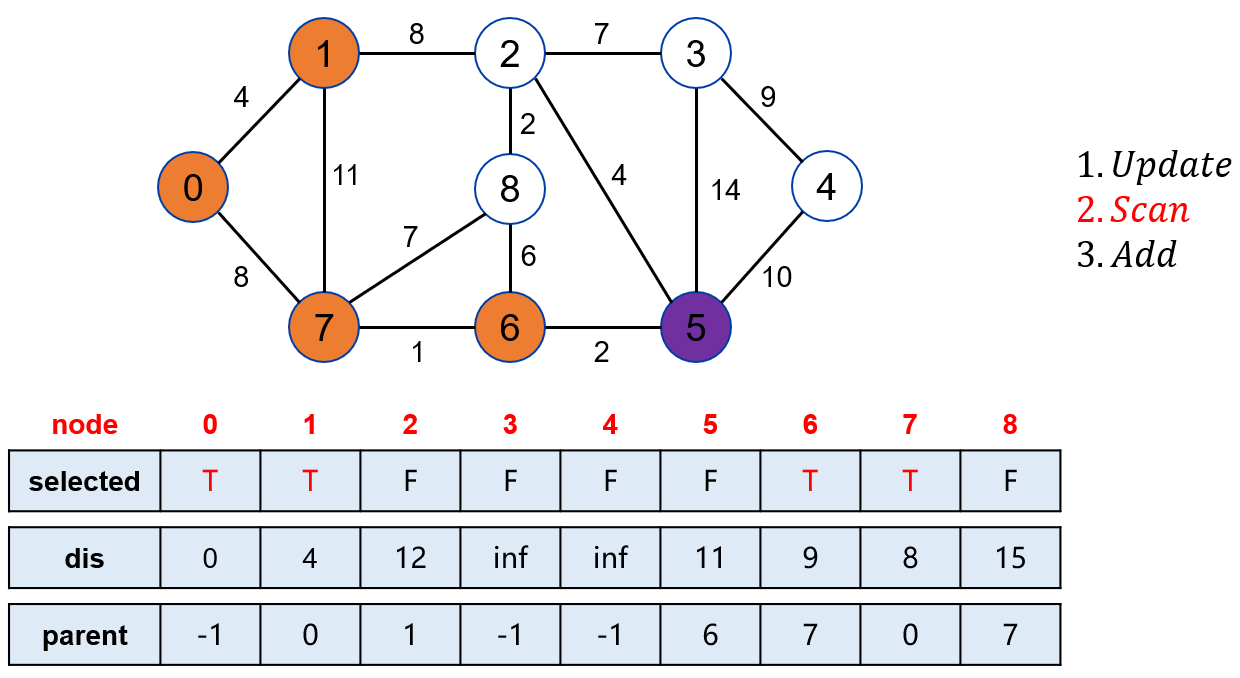
在未被标记的点中,找到距离起点最近的点是 5。
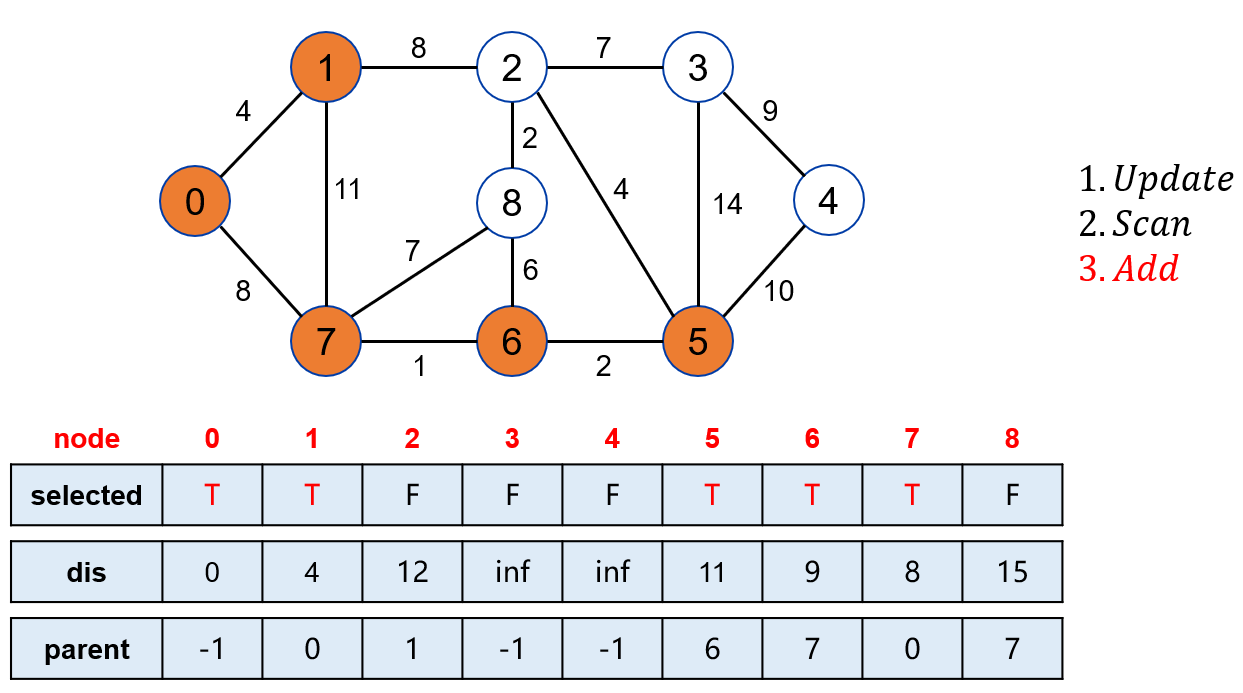
将点 5 标记。
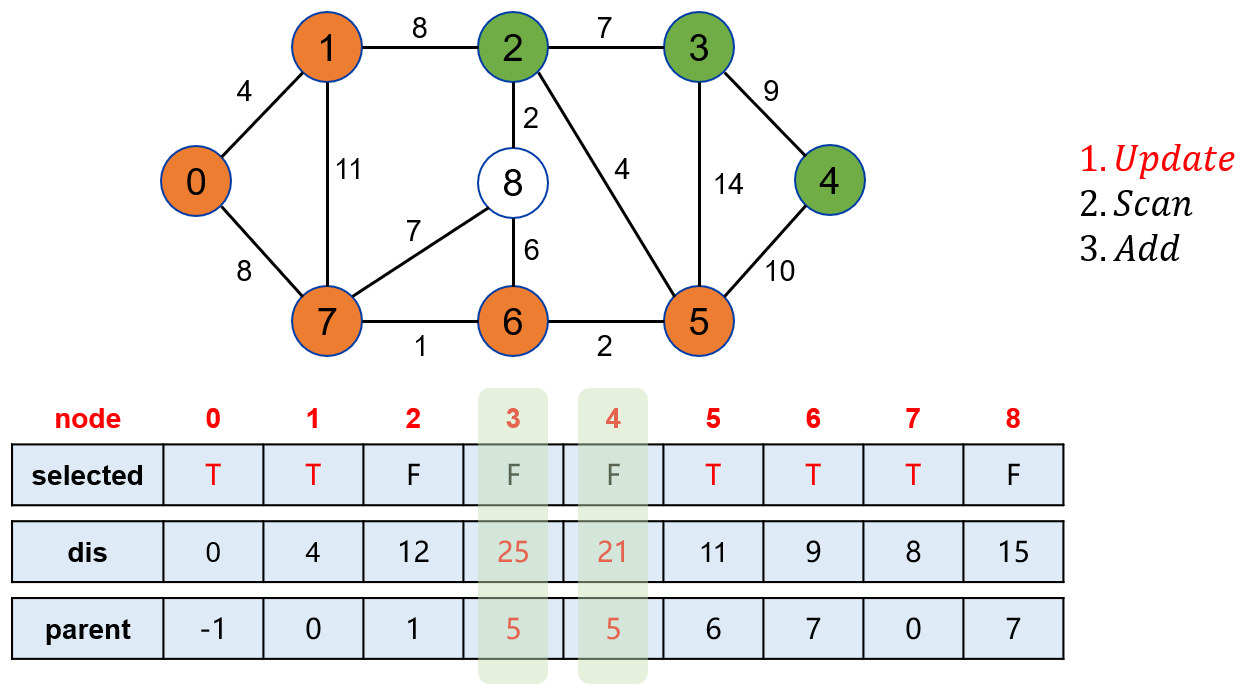
点 1 可以松弛操作点 2、点 3 和点 4。
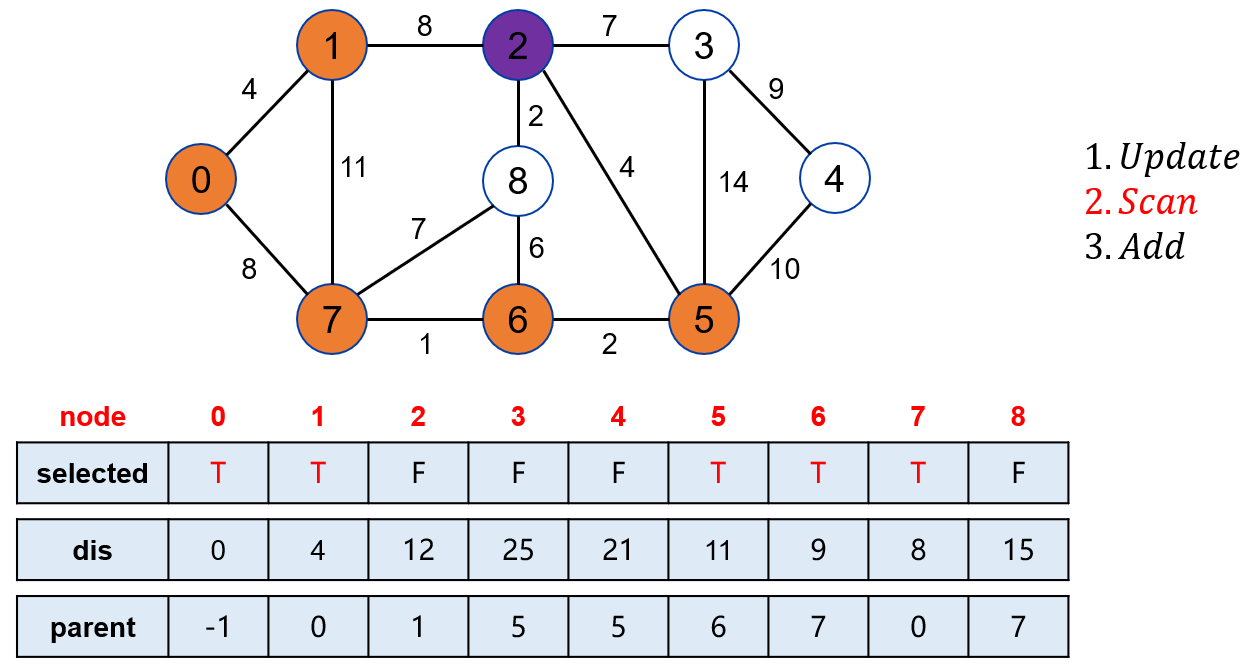
在未被标记的点中,找到距离起点最近的点是 2。
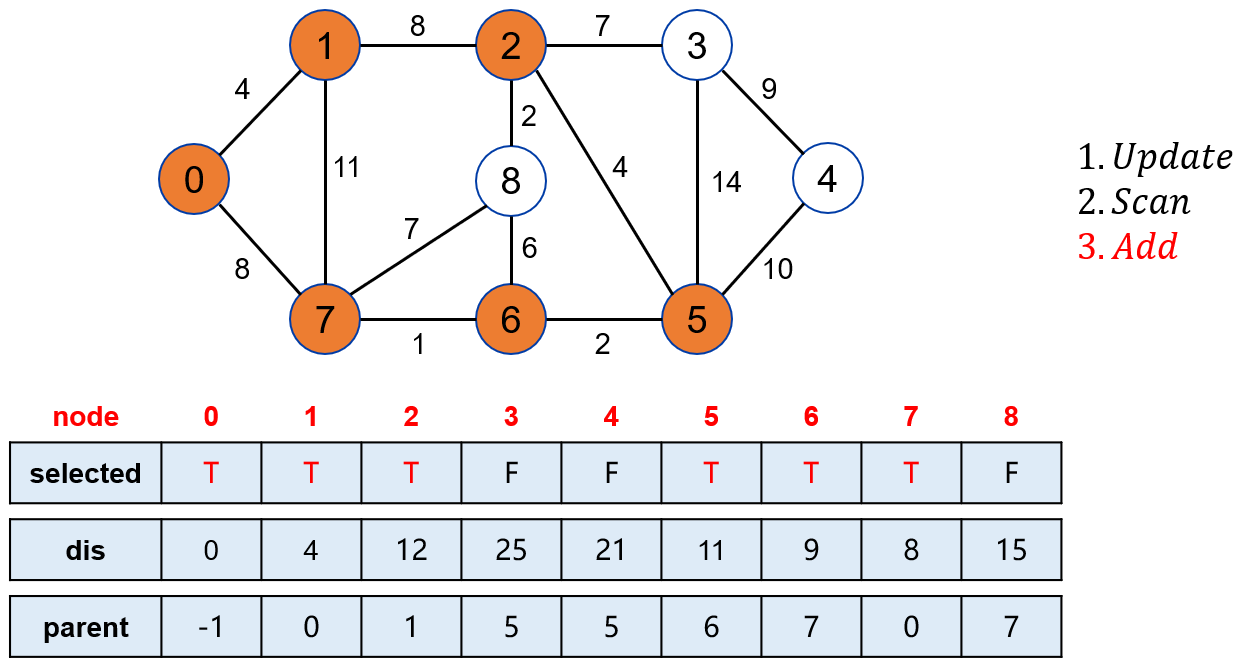
将点 2 标记。
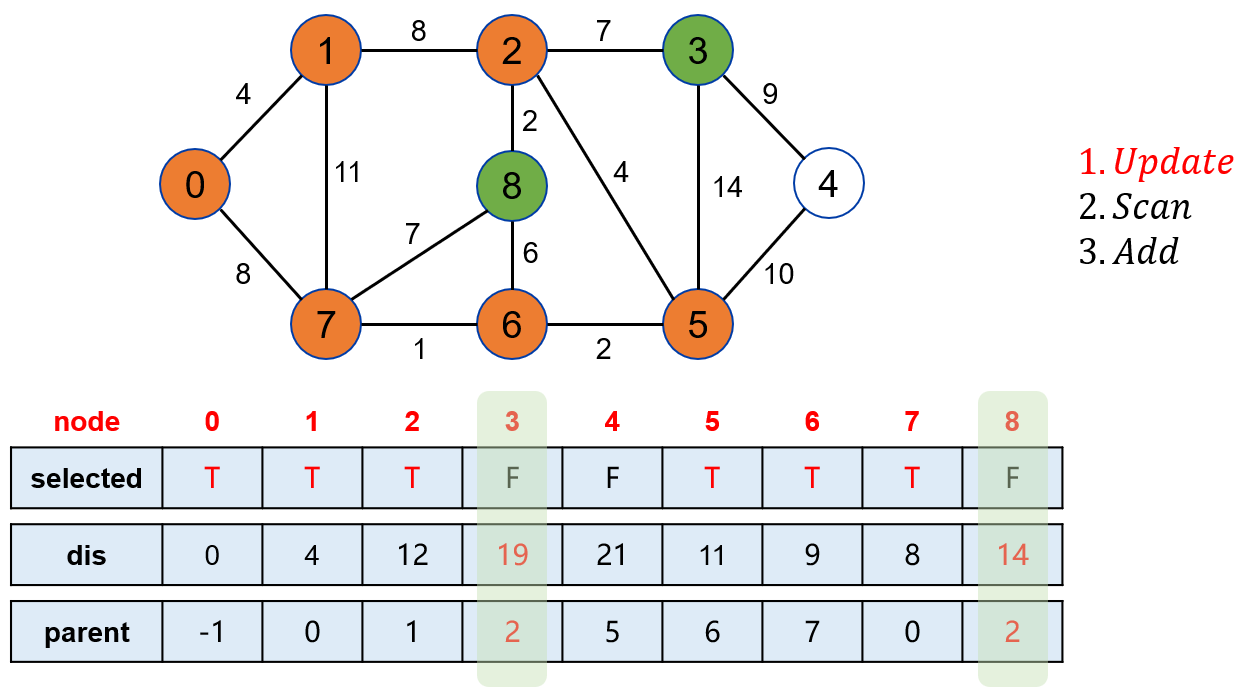
点 2 可以松弛操作点 3 和点 8。
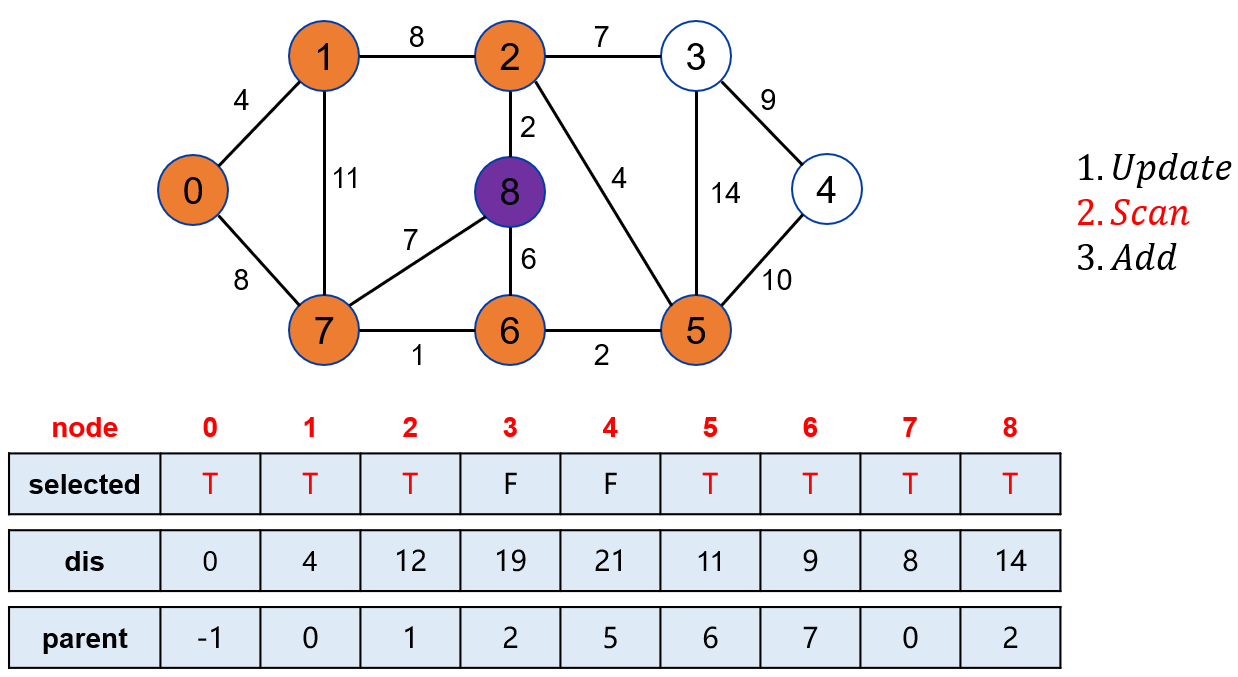
在未被标记的点中,找到距离起点最近的点是 8。

将点 8 标记。
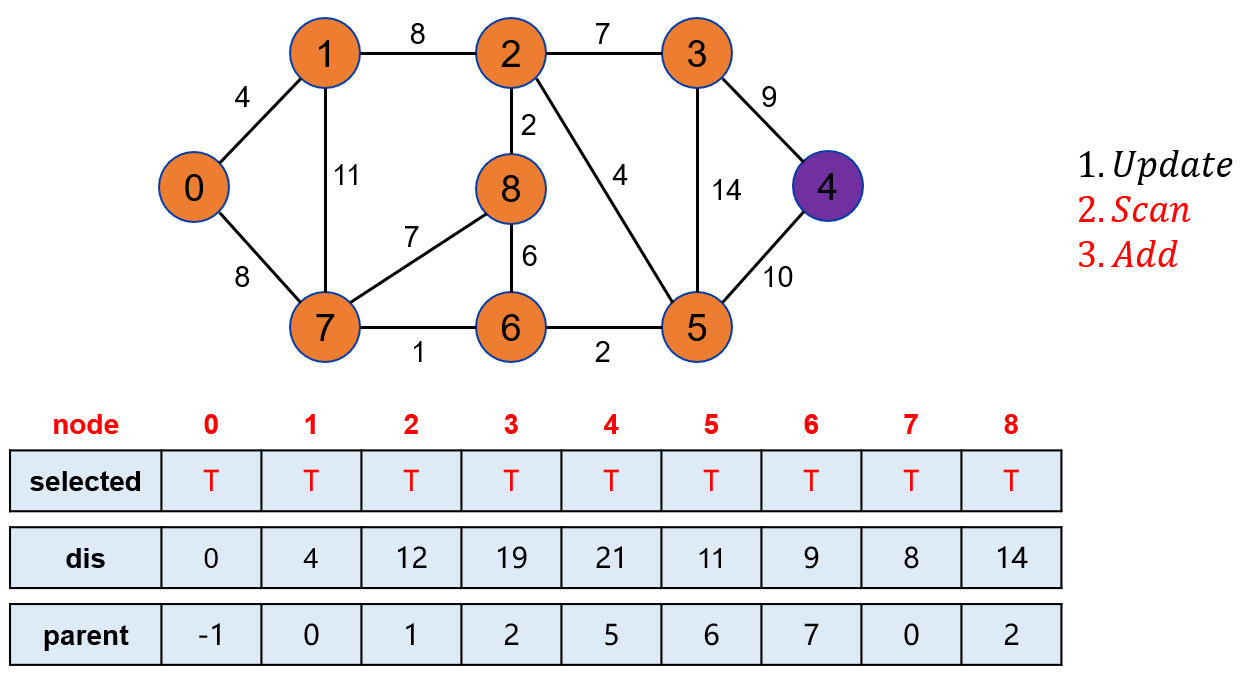
点 8 不能再松弛其它点,在未被标记的点中,找到距离起点最近的点是 4。
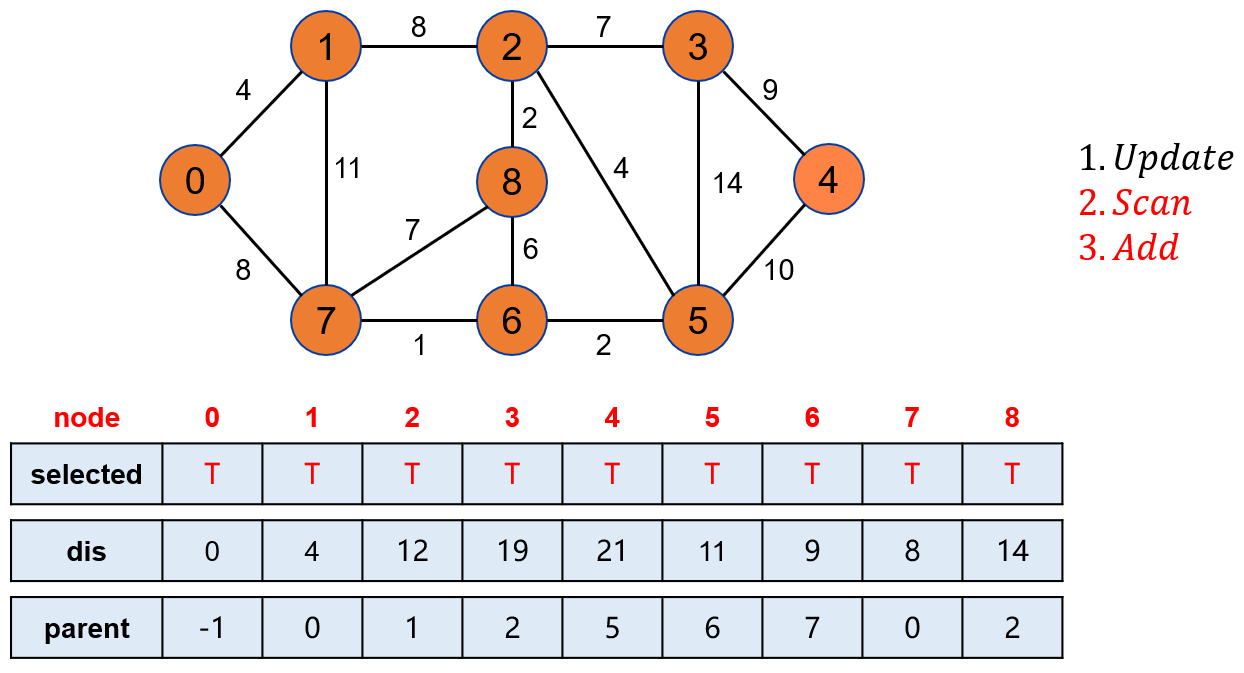
将点 4 标记。
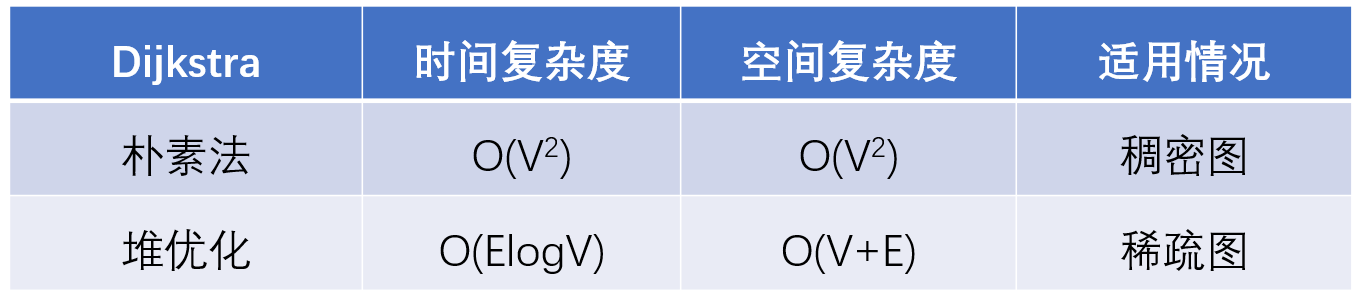
时间复杂度
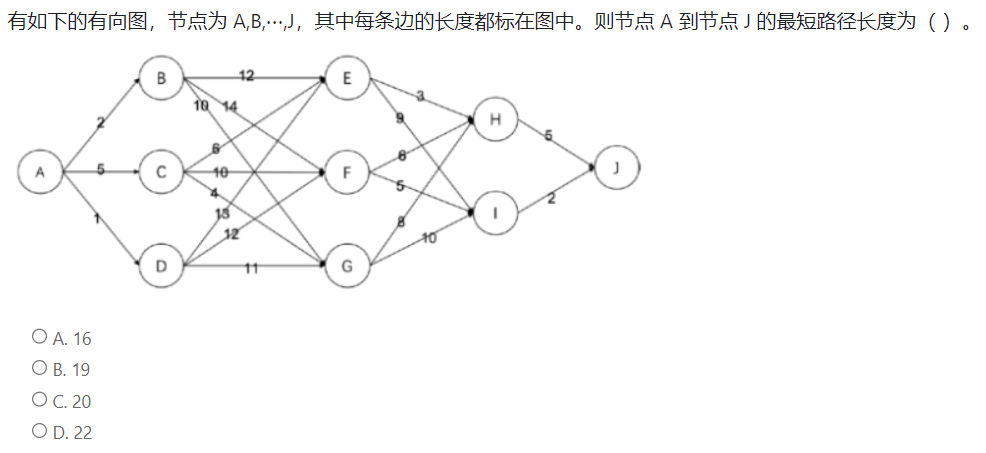
随堂检测
Dijkstra为什么边的权值不能为负数?
因为 Dijkstra 基于 BFS,计算过程是从起点 s 逐步扩散的过程,每扩散一次就用贪心法得到一个点的最短路径。扩散要求路径越来越长,如果遇到一条负边权,会导致路径变短,使扩散失效。
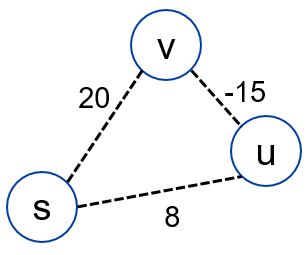
如图所示:设当前得到 s→u 的最短路径,路径长度为 8,此时 s→u 路径计算结束。继续扩展 u 的邻居,若 u 到邻居 v 的边权为 -15,而 v 到 s 距离为 20,那么 u 存在另一条途径到 s ,距离为 20+(-15)=5,这推翻了前面已经得到的长度为 8 的最短路径,破坏了 BFS 的扩散过程。
编程实战
单源最短路径朴素版
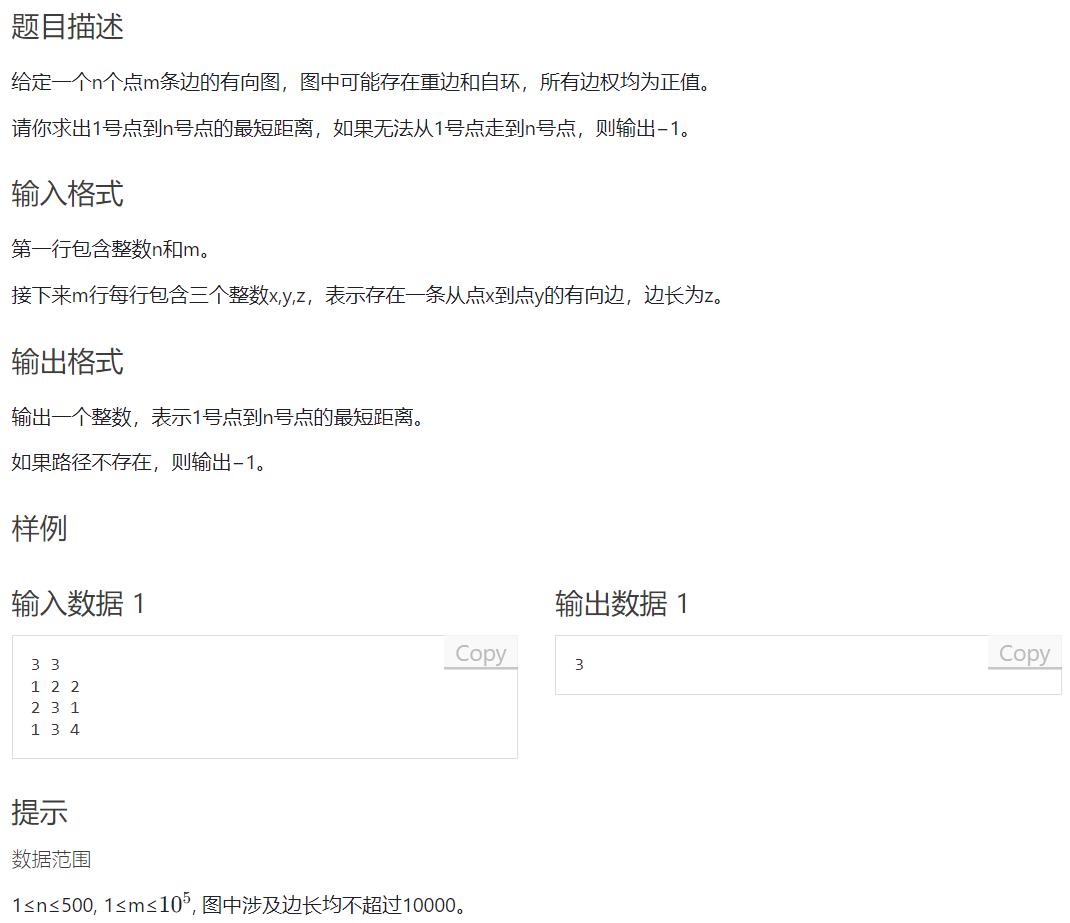
题目解析:邻接矩阵,时间复杂度 $O(N^2)$
参考程序:
#include <bits/stdc++.h>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int n, m;
int g[N][N];
int dis[N];
bool book[N];
int dijkstra(){
memset(dis, 0x3f, sizeof dis);
dis[1] = 0;
for(int i = 1; i <= n; i++){
int u = -1;
for(int j = 1; j <= n; j++){
if(!book[j] && (u == -1 || dis[j] < dis[u])){
u = j;
// dis[u] = dis[j];
}
}
book[u] = true;
for(int v = 1; v <= n; v++){
if(dis[v] > dis[u] + g[u][v])
dis[v] = dis[u] + g[u][v];
}
}
if(dis[n] == INF)
dis[n] = -1;
return dis[n];
}
int main(){
memset(g, 0x3f, sizeof g);
cin >> n >> m;
while(m--){
int a, b, c;
cin >> a >> b >> c;
g[a][b] = min(g[a][b], c);
}
for(int i = 1; i <= n; i++) g[i][i] = 0;
cout << dijkstra();
return 0;
}
单源最短路径进阶版

题目解析:邻接表,时间复杂度 $O(ElogN)$
参考程序:
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, INF = 0x3f3f3f3f;
typedef pair<int, int> PII;
struct Edge{
int w, to, next;
}edge[N];
int h[N];
int n, m;
int dis[N];
bool book[N];
int cnt = 0;
void add(int a, int b, int c){
edge[cnt].to = b;
edge[cnt].w = c;
edge[cnt].next = h[a];
h[a] = cnt++;
}
int dijkstra(){
memset(dis, 0x3f, sizeof dis);
dis[1] = 0;
priority_queue<PII, vector<PII>, greater<PII> > q;
q.push({0, 1});
while(q.size()){
PII t = q.top();
q.pop();
int u = t.second;
if(book[u]) continue;
book[u] = true;
for(int i = h[u]; ~i; i = edge[i].next){
int v = edge[i].to;
if(dis[v] > dis[u] + edge[i].w){
dis[v] = dis[u] + edge[i].w;
q.push({dis[v], v});
}
}
}
if(dis[n] == INF) dis[n] = -1;
return dis[n];
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while (m--) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
cout << dijkstra() << endl;
return 0;
}
城市路
