除法定理

对于任意正整数 a 和 任意正整数 m，存在唯一整数 q 和 r，满足 0≤r<m 且 a=qm+r，其中 $q=\lfloor\frac{a}{m}\rfloor$ 为商，r=a mod m 为余数。

同余定理

a mod m = b mod m，即 a,b 除以 m 所得的余数相等，记作：a $\equiv$​ b(mod m)。

欧拉函数

小于或等于 n 且与 n 互质的正整数的个数，称为欧拉函数，记为 φ(n)。

例如：φ(1)=1，φ(2)=1，φ(3)=2，φ(4)=2，φ(5)=4，φ(6)=2。

如果 n 是一个素数，那么 φ(n)=n-1。

定理：若 n 的质因数为 $p_1,p_2,...,p_s$，则欧拉函数表示为：$\phi(n)=n \prod_{i=1}^{s} (1-\frac{1}{p_i})$

例：$\phi(6)=6 \times (1-\frac{1}{2}) \times (1-\frac{1}{3})=2$

引理：如果 p 是一个质数，n 是一个正整数，那么 $\phi(p^n)=p^n-p^{n-1}$。

例如：p=3，n=2，$\phi(3^2)=3^2-3=6$。

乘法逆元

当 a,m 互素时，若 ax $\equiv$ 1(mod m)，则称 x 是 a 关于模 m 的逆元，记做 $a^{-1}$。在 $[0,m)$ 的范围内，逆元是唯一的。

证明

反证法：若 a 有两个逆元 0<$x_1$<$x_2$<m，即 $ax_1 \equiv ax_2 \equiv 1(mod) m$。

那么有 $m|a(x_2-x_1)$ 成立，又由于 (a,m)=1，因此 $m|(x_2-x_1)$，与 0<$x_1$<$x_2$​<m 矛盾。

费马小定理求逆元

欧拉定理：如果 (α, m)=1，则 $\alpha^{\phi(m)} \equiv 1$(mod m)

由 $\alpha \cdot \alpha^{\phi(m)-1} \equiv 1$(mod m)，可得 $\alpha^{\phi(m)-1} \equiv \alpha^{-1}$(mod m)

若 m 是素数：$\alpha^{m-2} \equiv \alpha^{-1}$(mod m)

// 快速幂求逆元
for(int i = 1; i <= n; i++)
    cout << quickPow(i, m - 2) << endl;

证明：

假设有 m-1 个整数，那么 α，2α，3α，...，(m-1)α 中没有一个是 m 的倍数，也不存在任意两个数模 m 同余。

因此，这 m-1 个数对模 m 的同余是 1,2,3，...，(m-1) 的全排列。

可以化简为：$\alpha^{m-1} \times (m-1)! \equiv (m-1)!$ (mod m)

即 $\alpha^{m-1} \equiv 1$ (mod m) 得证。

递推求逆元

设 i 为 [1,n] 中的整数，则 $p = \lfloor \frac{p}{i} \rfloor i$ + (p mod i)

从而有 $\frac{1}{i} \equiv - \frac{\lfloor \frac{p}{i} \rfloor}{p mod i}$ (mod) p

由于 p mod i < i，因此可以使用递推算法。

inv[i] = - (p / i) * inv[p % i] % p

最小正整数解：inv[i] = p - (p / i) * inv[p % i] % p

[NOIP 2011 提高组] 计算系数

参考程序

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 1010, MOD = 10007;

int a, b, k, n, m;
int fact[N] = {1}, invfact[N] = {1};

int quickPow(int a, int b)
{
    a %= MOD;
    int res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % MOD;
        a = a * a % MOD;
        b >>= 1;
    }

    return res;
}

int main()
{

    cin >> a >> b >> k >> n >> m;

    for (int i = 1; i <= k; i++)
    {
        fact[i] = fact[i - 1] * i % MOD;
        invfact[i] = invfact[i - 1] * quickPow(i, MOD - 2) % MOD;
    }

    int t = fact[k] * invfact[n] % MOD * invfact[k - n] % MOD;

    cout << t * quickPow(a, n) % MOD * quickPow(b, m) % MOD << endl;

    return 0;
}

卡特兰数

在一个二维平面内，从 (0, 0) 出发到达 (n, n)，每次可以向上或者向右走一格，0 代表向右走一个，1 代表向上走一格，则每条路径都会代表一个 01 序列，则满足任意前缀中 0 的个数不少于 1 个数序列对应的路径则右下侧。

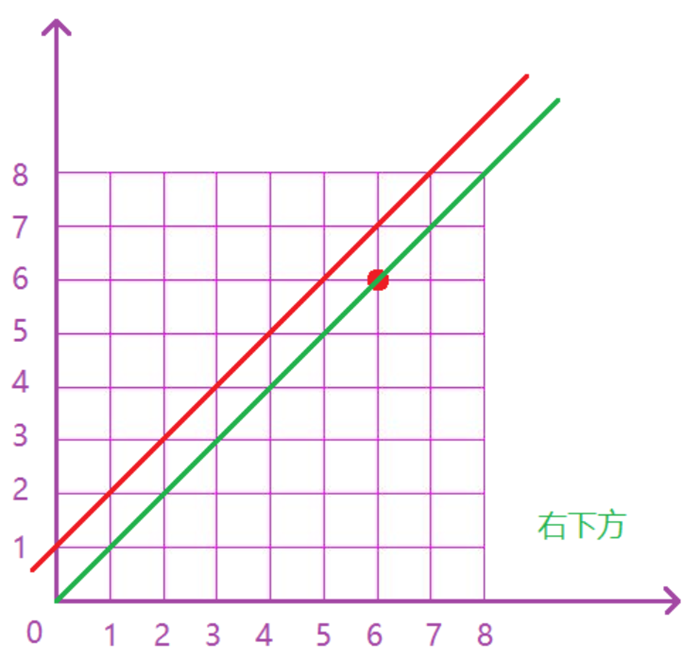
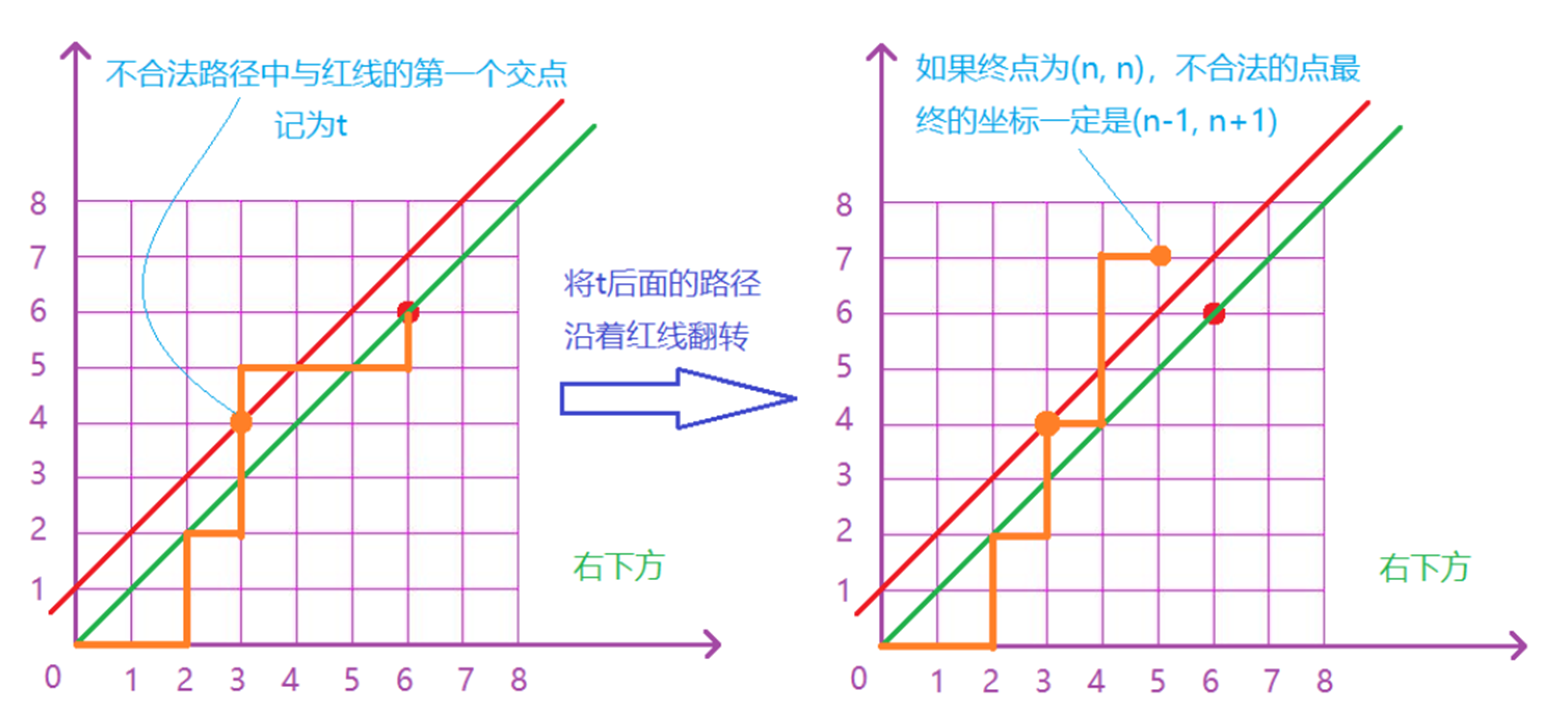
[NOIP 2003 普及组] 栈

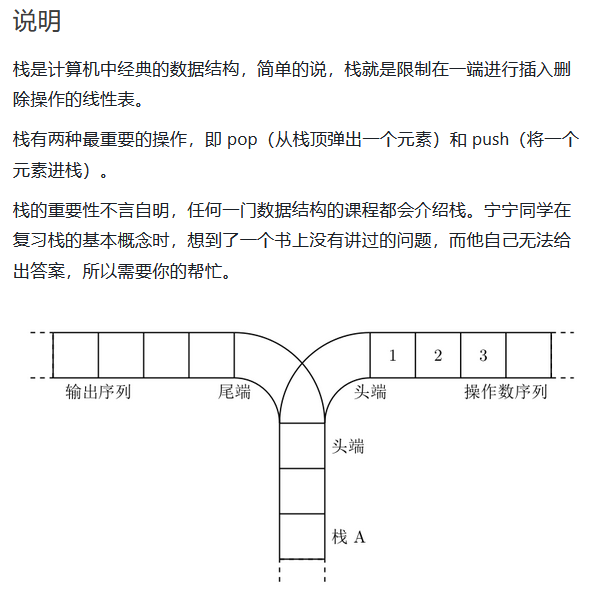
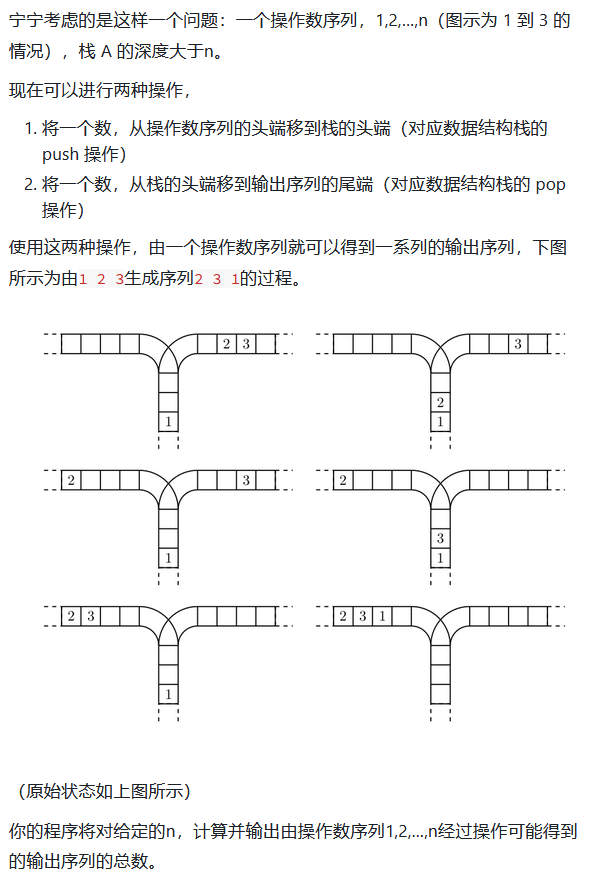
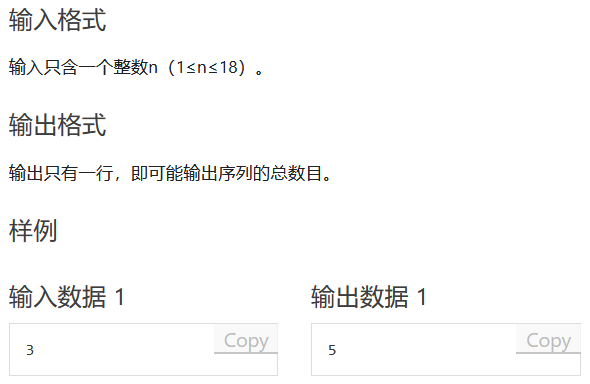
题目解析

答案是卡特兰数。$\frac{C_{2n}^n}{n+1}$

使用组合数递推公式：$C_n^m=C_n^{m-1}+C_{n-1}^{m-1}$，即杨辉三角。

参考程序

#include <iostream>
#include <cstdio>
using namespace std;

// C(2n,n)/(n+1)
// 二叉树不同形态数量、合法括号匹配数量、凸n变形可以划分成三角形个数 卡特兰数

typedef long long LL;

const int N = 40;

int n;
LL C[N][N];

int main() {

      cin >> n;

      for(int i = 0; i <= 2 * n; i++)
        for(int j = 0; j <= i; j++)
              if(!j) C[i][j] = 1;
              else C[i][j] = C[i - 1][j] + C[i - 1][j - 1];

      cout << C[2 * n][n] / (n + 1) << endl;

    return 0;
}

构造排列

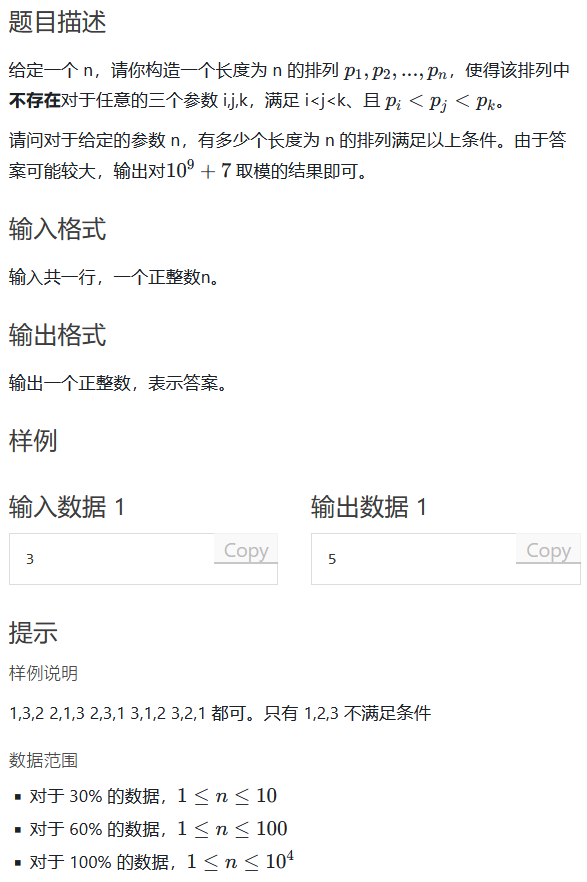
题目解析

答案是卡特兰数。$\frac{C_{2n}^n}{n+1}$

由于数据范围较大，使用快速幂和逆元求解。

参考程序

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 200010, MOD = 1e9 + 7;
typedef long long LL;

int n;
int fact[N] = {1}, invfact[N] = {1};

int qmi(int a, int k) {
    int res = 1;
    while (k) {
        if (k & 1) res = (LL)res * a % MOD;
        a = (LL)a * a % MOD;
        k >>= 1;
    }
    return res;
}

int main()
{

    cin >> n;

    for (int i = 1; i < N; i++)
    {
        fact[i] = (LL)fact[i - 1] * i % MOD;
        invfact[i] = (LL)invfact[i - 1] * qmi(i, MOD - 2) % MOD;
    }

    cout << (LL)fact[2 * n] * invfact[n] % MOD * invfact[n] % MOD * qmi(n + 1, MOD - 2) % MOD << endl;

    return 0;
}