五级大纲

  • 数组模拟高精度加法、减法、乘法、除法
  • 单链表、双链表、循环链表
  • 辗转相除法（也称欧几里得算法）
  • 素数表的埃氏筛法和线性筛法
  • 唯一分解定理
  • 二分查找/二分答案（也称二分枚举法）
  • 贪心算法
  • 分治算法（归并排序和快速排序）
  • 递归
  • 算法复杂度的估算（含多项式、指数、对数复杂度）

知识点解析

高精度算法

高精度加法

vector<int> add(vector<int>& A, vector<int>& B){
    vector<int> C;

    if(A.size() < B.size()) return add(B, A);

    int k = 0; // 进位
    for(int i = 0; i < A.size(); i++){
        int t = A[i] + k;
        if(i < B.size()) t += B[i];
        C.push_back(t % 10);
        k = t / 10;
    }

    if(k) C.push_back(1);

    while(C.back() == 0 && C.size() > 1) C.pop_back();
    return C;
}

高精度减法

vector<int> sub(vector<int>& A, vector<int>& B) {
    vector<int> C;
    if (!cmp(A, B)) {
        cout << "-";
        return sub(B, A);
    }

    int k = 0;
    for (int i = 0; i < A.size(); i++) {
        int t = A[i] - k;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) k = 1;
        else k = 0;
    }

    while (!C.back() && C.size() > 1) C.pop_back();

    return C;
}

高精乘单精

vector<int> mul(vector<int>& A, int b) {
    vector<int> C;

    int k = 0;
    for (int i = 0; i < A.size() || k; i++) {
        int t;
        if (i < A.size()) t = A[i] * b + k;
        else t = k;

        k = t / 10;
        C.push_back(t % 10);
    }

    while (!C.back() && C.size() > 1) C.pop_back();

    return C;
}

高精乘高精

vector<int> mul(vector<int>& A, vector<int>& B) {
    vector<int> C(A.size() + B.size() + 10);

    for (int i = 0; i < B.size(); i++)
        for (int j = 0; j < A.size(); j++)
            C[i + j] += B[i] * A[j];

    int t = 0;
    for (int i = 0; i < C.size(); i++) {
        t += C[i];
        C[i] = t % 10;
        t /= 10;
    }

    while (!C.back() && C.size() > 1) C.pop_back();

    return C;
}

高精除单精

vector<int> div(vector<int>& A, int b, int& r) {

    vector<int> C;

    for (int i = 0; i < A.size(); i++) {
        int t = r * 10 + A[i];
        C.push_back(t / b);
        r = t % b;
    }

    reverse(C.begin(), C.end());

    while (!C.back() && C.size() > 1) C.pop_back();

    return C;
}

高精除高精

vector<int> div(vector<int>& A, vector<int>& B, vector<int>& R) {
    vector<int> C;

    int j = B.size();
    R.assign(A.end() - j, A.end());

    while (j <= A.size()) {
        int k = 0;
        while (cmp(R, B)) {
            vector<int> tmp = sub(R, B);
            R.assign(tmp.begin(), tmp.end());
            k++;
        }
        C.push_back(k);
        if (j < A.size()) R.insert(R.begin(), A[A.size() - j - 1]);
        while (!R.back() && R.size() > 1) R.pop_back();
        j++;
    }

    reverse(C.begin(), C.end());

    while (!C.back() && C.size() > 1) C.pop_back();

    return C;
}

链表

链表相较于数组，可以充分利用内存中分散的空间，但是每个节点都至少需要一个指针，我们可以用 class 封装一个动态链表。

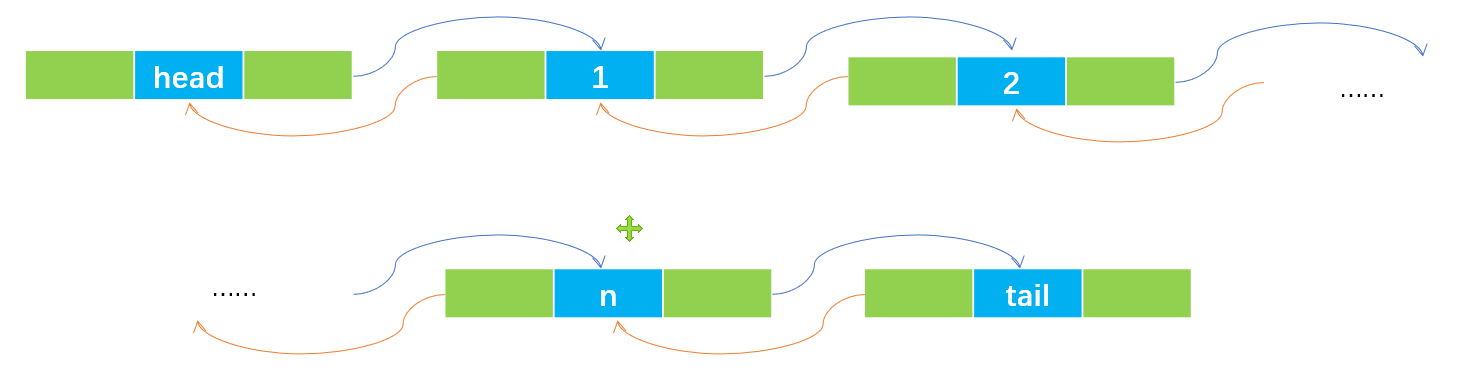
双向链表结点

template<class T>
struct ListNode {
    T data;
    ListNode* next;
    ListNode* prior;
};

一个数据域，一个向后指针域，一个向前指针域。

循环链表：链表的尾结点的 next 指针指向头结点。

基础数论

约数、倍数、素数、合数

约数（Divisors 或 Factors）

定义：如果一个整数 a 除以另一个非零整数 b，商为整数，且余数为零，我们就说 b 是 a 的约数。

解释：

约数也叫因数。

一个数的约数总是成对出现的（除了完全平方数，其平方根只出现一次）。

例子：6 的约数有 1、2、3 和 6，因为 6 可以被这些数整除。

倍数（Multiples）

定义：如果 a 和 b 都是整数，且 b 不是 0，那么 b 是 a 的倍数当且仅当 a 除以 b 的余数为 0。

解释：

一个数的倍数是无限多的，除非这个数是 0（0 没有正倍数）。

任何数都是 1 和它本身的倍数。

例子：3 的倍数有 3、6、9、12、15 等，因为这些都是 3 的整数倍。

素数（Prime Numbers）

定义：一个大于 1 的自然数，除了 1 和它自身外，无法被其他自然数整除的数叫做素数。

解释：

素数只有两个正因数：1 和它自己。

最小的素数是 2。

例子：2、3、5、7、11、13、17、19 等都是素数。

合数（Composite Numbers）

定义：除了 1 和它本身以外还有其他因数的数叫做合数。

解释：

合数至少有三个正因数。

1 和所有素数都不是合数。

例子：4、6、8、9、10、12 等都是合数（因为它们除了 1 和自己外，还有其他因数）。

辗转相除法

求 6731 和 2809 的最大公因数：

6731 = 2809*2 + 1113

2809 = 1113*2 + 583

1113 = 583*1 + 530

583 = 530 + 53

530 = 53*10 + 0

所以 (6731,2809)= 53

int gcd(int a, int b){
    return b ? gcd(b, a % b) : a;
}

复杂度为 O(log(max(a,b))。

由于任何正整数都是 0 和 0 的公约数，故 gcd(0, 0) 不存在。

对任意正整数 a，有 gcd(0, a) = a。

素数筛法

埃式筛法：（Eratosthenes筛法）只有质数才可能标记后面的合数。

时间复杂度：O(nloglogn)。

vector<int> get_primes(int n){

    vector<int> v;    

    for(int i = 2; i <= n; i++){
        if(!book[i]) {
            v.push_back(i);

            for(int j = 2 * i; j <= n; j += i)
                book[j] = true;
        } 
    }

    return v;
}

欧拉筛法：（线性筛法）设 x 的最小质因数为 d，则 x 只会被 xd\frac{x}{d} 标记。

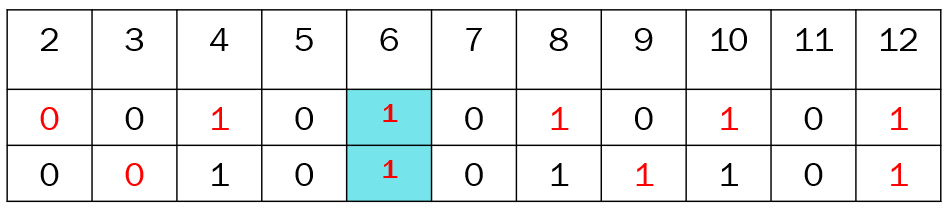
时间复杂度 O(n)。

当枚举到 i 时，假设当前已经求出质数为 P1,P2,…,PkP_1,P_2,\ldots,P_k，而 i 的最小质因数为 PmP_m，则对于所有的 x∈[1,m]，PxiP_x i 的最小质因数就是 PxP_x，故用 i 标记 PxiP_x i。

vector<int> get_primes(int n){
    vector<int> v;
      for(int i = 2; i <= n; i++){
        if(!book[i]) v.push_back(i);
          for(int j = 0; v[j] <= n / i; j++){
            book[v[j] * i] = true;
              if(i % v[j] == 0) break;
        }
    }
      return v;
}

唯一分解定理

设 n≥2 为整数，则有唯一的分解式：n=∏i=1mPiαin = \prod\limits_{i=1}^m {P_i}^{\alpha_i}，其中 P1<P2<…<PmP_1<P_2<\ldots<P_m 且 PiP_i 为质数，αi\alpha_i 为正整数。

相关题目

01-特殊的质数肋骨

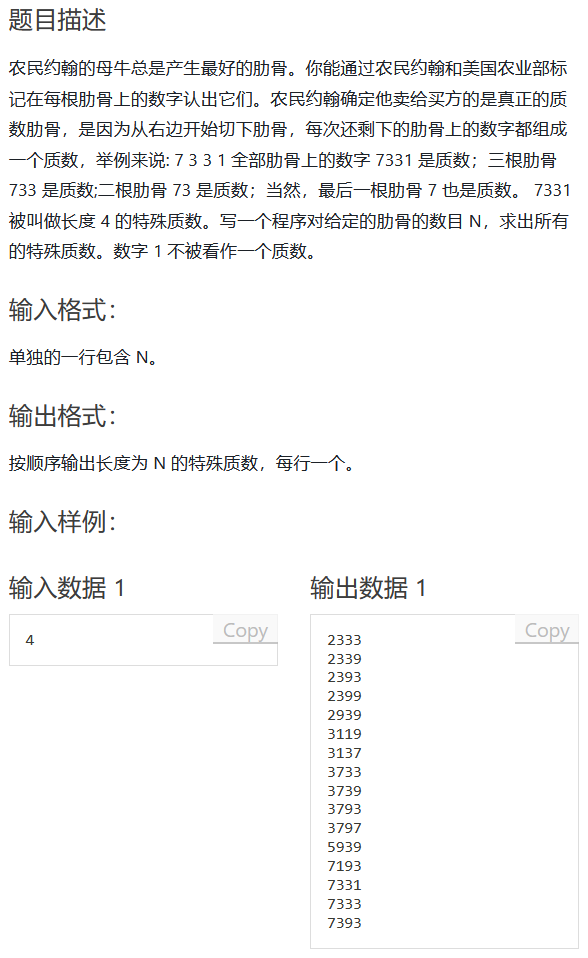
  • 暴力枚举：先用埃氏筛打表，然后直接输出结果。
#include <bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    cin >> n;
    switch (n)
    {
    case 1:
        cout << "2\n3\n5\n7";
        break;
    case 2:
        cout << "23\n29\n31\n37\n53\n59\n71\n73\n79\n";
        break;
    case 3:
        cout << "233\n239\n293\n311\n313\n317\n373\n379\n593\n599\n719\n733\n739\n797\n";
        break;
    case 4:
        cout << "2333\n2339\n2393\n2399\n2939\n3119\n3137\n3733\n3739\n3793\n3797\n5939\n7193\n7331\n7333\n7393";
        break;
    case 5:
        cout << "23333\n23339\n23399\n23993\n29399\n31193\n31379\n37337\n37339\n37397\n59393\n59399\n71933\n73331\n73939";
        break;
    case 6:
        cout << "233993\n239933\n293999\n373379\n373393\n593933\n593993\n719333\n739391\n739393\n739397\n739399";
        break;
    case 7:
        cout << "2339933\n2399333\n2939999\n3733799\n5939333\n7393913\n7393931\n7393933";
        break;
    case 8:
        cout << "23399339\n29399999\n37337999\n59393339\n73939133";
        break;
    }
    return 0;
}

02-约数研究

#include <iostream>
#include <cstdio>
using namespace std;

int n, res = 0;

int main() {

      cin >> n;
      for(int i = 1; i <= n; i++) res += n / i;

      cout << res << endl;

    return 0;
}

二分法

二分查找

int L = 1, R = n;

while(L <= R){
    int m = L + R >> 1;
    if(a[m] == x){
        cout << "YES" << endl;
        return 0;
    }

    if(a[m] > x) L = m + 1;
    else R = m - 1;
}

cout << "NO" << endl;

二分答案

求满足某条件的最小值

// check()函数：判断某答案是否满足条件

while(L < R) {
    int mid = (L + R) / 2;
    if(check(mid)) //如果满足条件，看左半部分
        R = mid;
    else
        L = mid + 1;
}

求满足某条件的最大值

while(L < R) {
    int mid = (L + R + 1) / 2;
    if(check(mid)) //如果满足某一条件，看右半部分
        L = mid;
    else
        R = mid - 1;
}

函数指针

函数存放在内存的代码区域内，它们同样有地址.如果我们有一个 int f(int n) 的函数，那么，它的地址就是函数的名字，这一点如同数组一样，数组的名字就是数组的起始地址。

1：函数指针定义方式

data_types (*func_pointer)( data_types arg1, data_types arg2, ...,data_types argn);

#include <bits/stdc++.h>
using namespace std;

int f(int n){
    return n;
}

int main() {

    int (*fp)(int n);

    fp = f;

    cout << f(10) << endl;

    return 0;
}

注意：函数指针所指向的函数一定要保持函数的返回值类型，函数参数个数，类型一致。

2：typedef 简化函数指针定义

#include <bits/stdc++.h>
using namespace std;

int f(int n){
    return n;
}

int main() {

    typedef int (*fp)(int n);

    fp f2 = f;
    fp f3 = f;

    cout << f2(10) << endl;
    cout << f3(20) << endl;

    return 0;
}

3：函数指针作为函数参数

#include <bits/stdc++.h>
using namespace std;

int f(int n){
    return n;
}

int f2(int (*f)(int), int n){
    int r = f(10) + n;
    return r;
}

int main() {

    cout << f2(f, 5) << endl;

    return 0;
}

4：函数指针数组

#include <bits/stdc++.h>
using namespace std;

void f1(){
    puts("f1");
}

void f2(){
    puts("f2");
}

void f3(){
    puts("f3");
}

int main() {

    typedef void (*fp)(void);

    fp f[3] = {f1, f2, f3};
    f[0]();

    return 0;
}

results matching ""

    No results matching ""