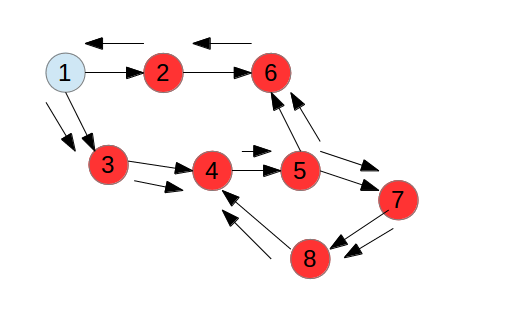
边集数组
边集数组是由两个一维数组构成。
一个是存储顶点的信息,另一个是存储边的信息。边数组每个数据元素由一条边的起点下标 (begin), 终点下标 (end) 和权 (weight) 组成。
边集数组关注的是边的集合,对顶点的处理效率较低,例如查找某顶点的度,就需要扫描整个边数组。
链式前向星
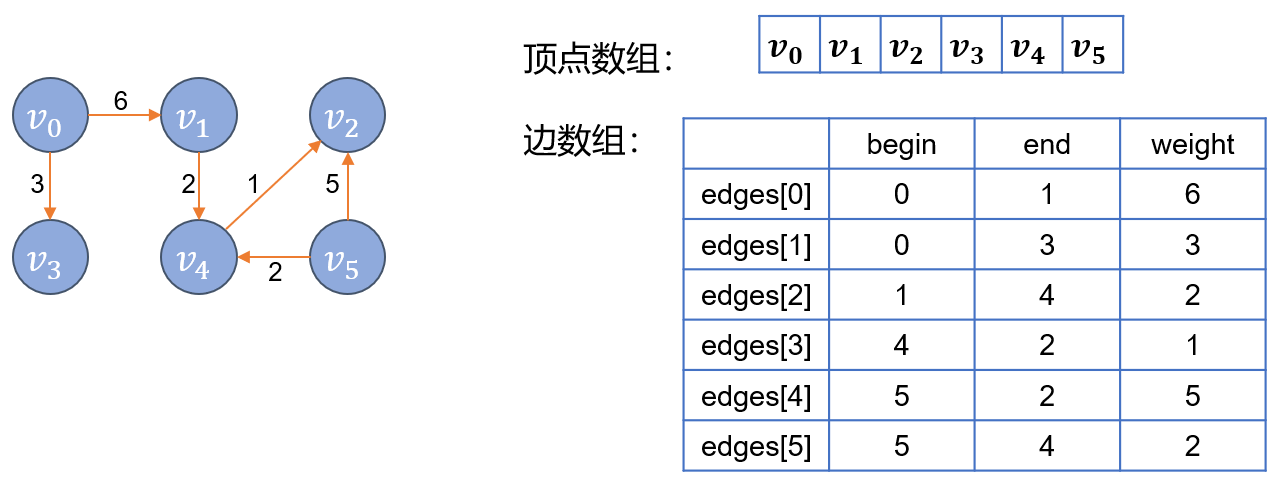
链式前向星可用于存储图,本质上是一个静态链表,用边集数组和邻接表相结合,可用快速访问一个顶点所有邻接点。
链式前向星存储包括两种结构:
边数组:edge[] ,edge[i] 表示第 i 条边。
头结点数组:head[],head[i] 存以 i 为起点的最后一条边的下标(在edge[]中的下标)。
使用链式前向星,储存 N 个顶点的有向有权图,边集数组对应的边数 M 未指定的情况下,要设置比 NN 大的数(无向图需要再 2 )。
头结点数组 head[a]=i,表示顶点 a 的最后一个邻接边是 edge[i]。

链式前向星的特性:
和邻接表一样,因为采用头插法进行链接,所以边输入顺序不同,创建的链式前向星也不同。
对于无向图,每输入一条边,需要添加两条边,互为反向边。例如,输入第一条边 1 2 5,实际上添加了两条边,如图所示:

如果一条边的下标为 i,则其反向边为 i^1 。
- 链式前向星具有边集数组和邻接表的功能,属于静态链表,不需要频繁地创建结点,应用十分灵活。
struct Edge{
int to, w, next;
}edge[M];
int h[N];
int cnt = 0;
void add(int a, int b, int c){
edge[cnt].to = b;
edge[cnt].w = c;
edge[cnt].next = h[a];
h[a] = cnt++;
}
memset(h, -1, sizeof h);
for(int i = h[x]; ~i; i = edge[i].next){
int to = edge[i].to;
}
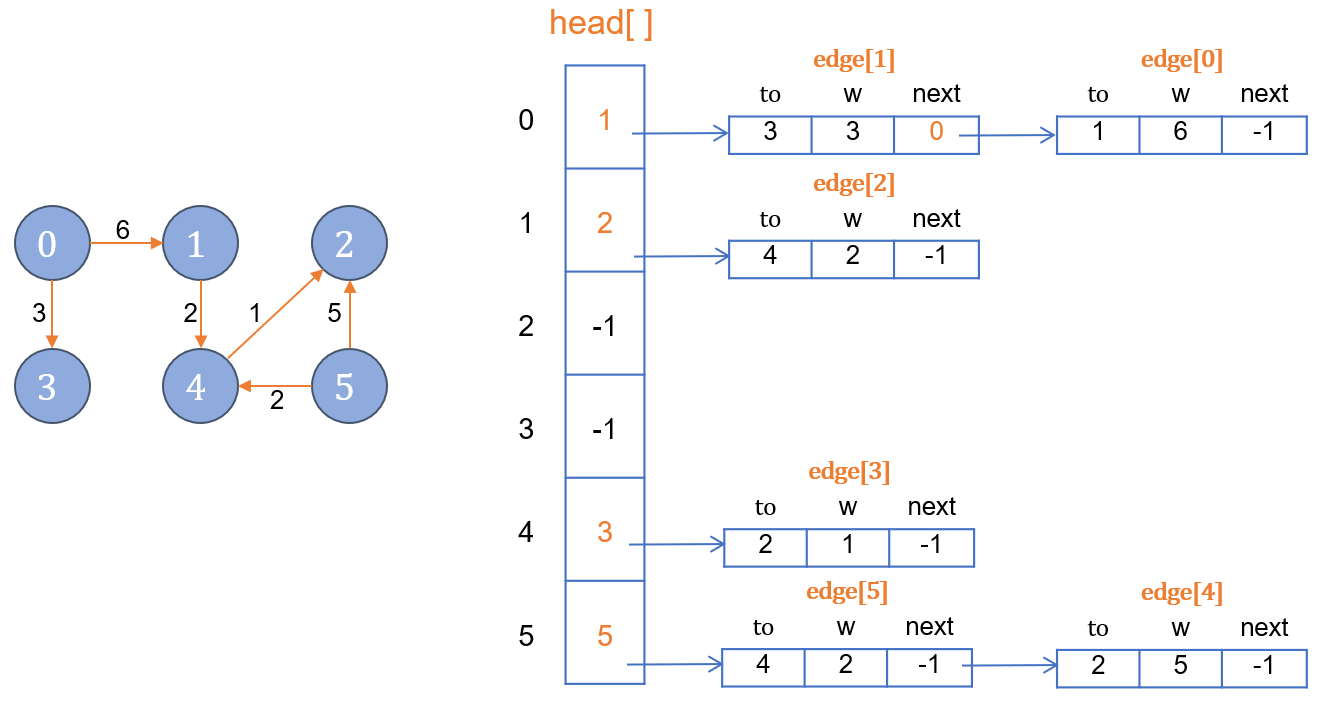
无向图判断是否有环:深搜
除了“父顶点”,邻接点中有标记过的顶点就是有环。
例:
从顶点1开始深搜,访问2,访问3,
访问4时,4的“父顶点”是3,除了3外,1是已经访问过的顶点,所以存在环。
有向图判断是否有环:深搜 + 3色标记
每个顶点有3种标记
0:该顶点未访问过
-1:该顶点的邻接点未访问完
1:该顶点的邻接点已访问完
深度优先遍历有向图,如果一个顶点的邻接点有标记为-1的顶点,那么该图中存在环。
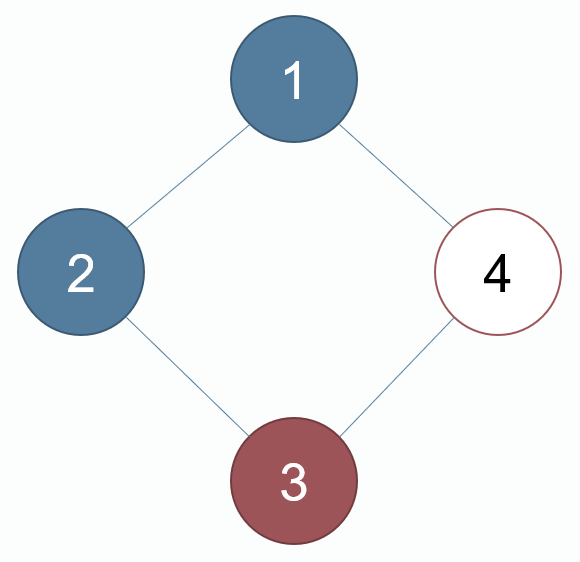
如图所示,是一个有向无环图:
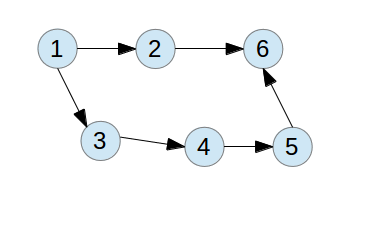
如图所示,是一个有向有环图:
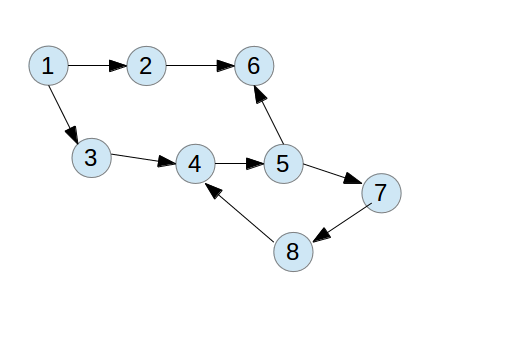
假定我们从结点1出发,先访问2这边的边,一直到结点6,这个时候按照深度优先遍历是首先一步步递归进去到结点6。因为结点6没有别的出边,所以就要一步步的按照前面的过程返回。
具体过程:结点1被标记为-1,继续深搜遍历结点2、结点6,然后返回。
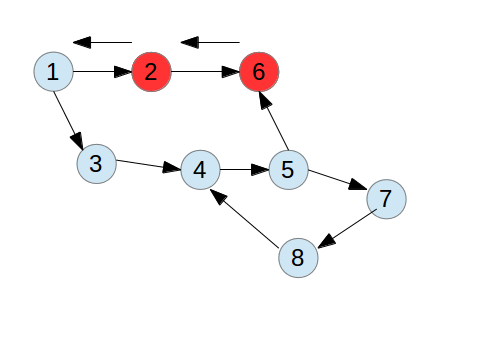
在前面2,6结点都返回后,这个时候就算后面的结点比如5访问到6了,它们是不构成环的。
具体过程:结点1还是被标记为-1,继续深搜遍历结点3、结点4、结点5、结点6,然后返回,当结点1已经没有其他邻接点了,就可以标记为1。
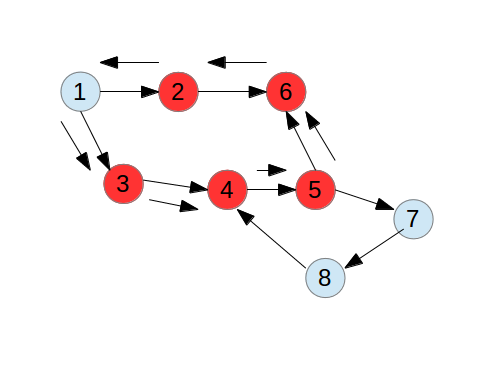
当前状态:访问到结点4,被标记为-1,深搜遍历结点5、结点7、结点8。
此时,结点4还是标记为-1,而结点8的下一个点就是结点4,构成环。