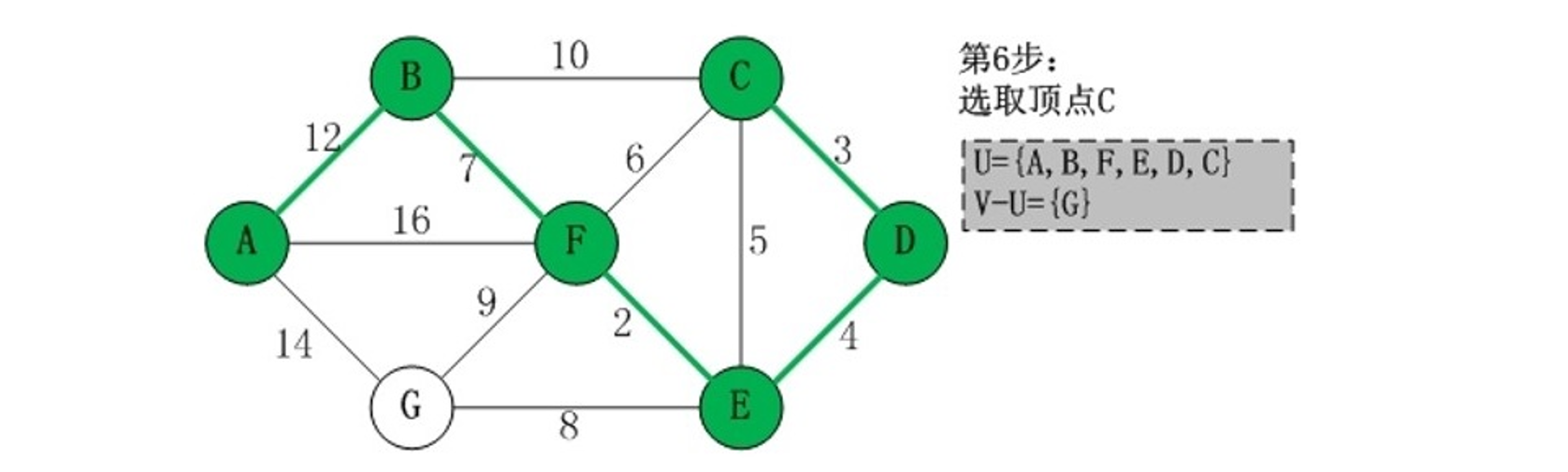
最短路径问题

最短路径问题：如果从图中某一顶点（源点）到达另一顶点（终点）的路径可能不止一条，如何找到一条路径使得沿此路径上各边的权值总和（称为路径长度）达到最小。

单源最短路径问题：计算从源点到其他所有顶点的最短路径长度。

多源最短路径问题：计算从所有顶点到所有顶点的最短路径长度。

Floyd算法

Floyd-Warshall 算法：又称为插点法，是一种利用动态规划的思想求多源最短路径的算法。

图中可以有正权边或负权边，但是不能有负权回路。

算法思想：

状态定义：$g[k][i][j]$：只能使用第1号到第k号点作为中间媒介时，点i到点j之间的最短路径长度。

初始条件：如果存在弧，$g[0][i][j]$ = w(i, j) i到j弧的权值如果不存在弧，$g[0][i][j]$ = INF

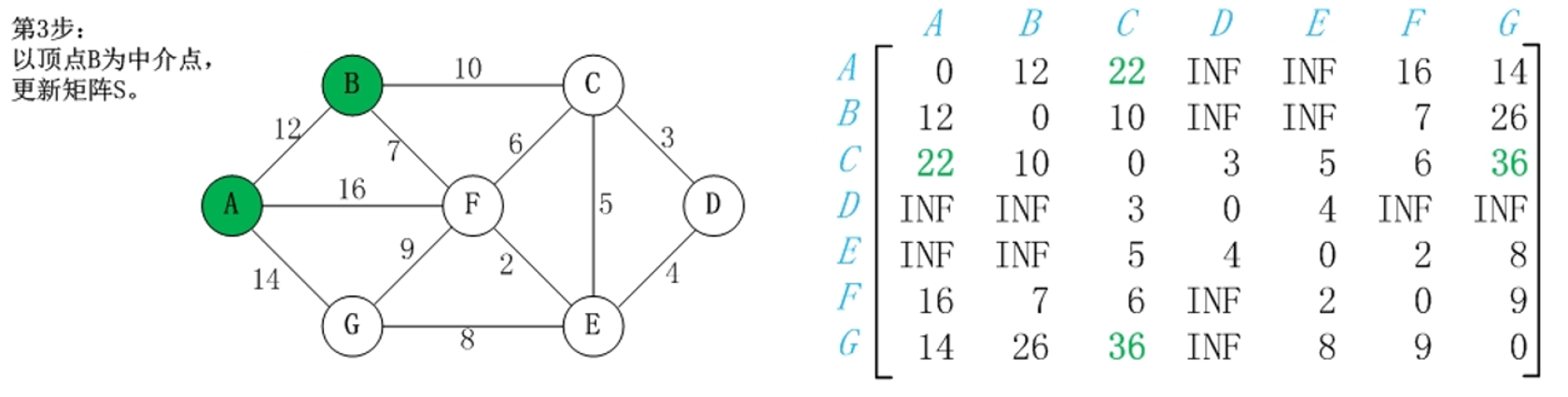
状态转移方程：$g[k][i][j] = min(g[k-1][i][j], g[k-1][i][k] + g[k-1][k][j])$

数组降维：$g[i][j] = min(g[i][j], g[i][k] + g[k][j])$

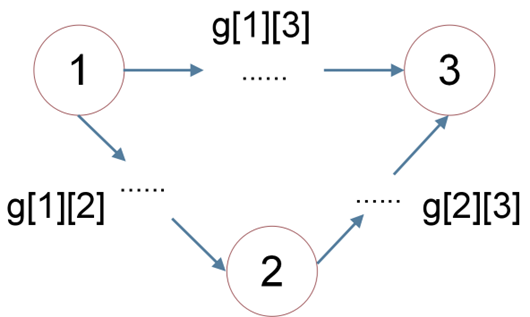
如果 $g[1][3] > g[1][2] + g[2][3]$

那么 $g[1][3] = g[1][2] + g[2][3]$

for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                g[i][j] = min(g[i][j], g[i][k] + g[k][j]);

Floyed的时间复杂度是 $O(N^3)$

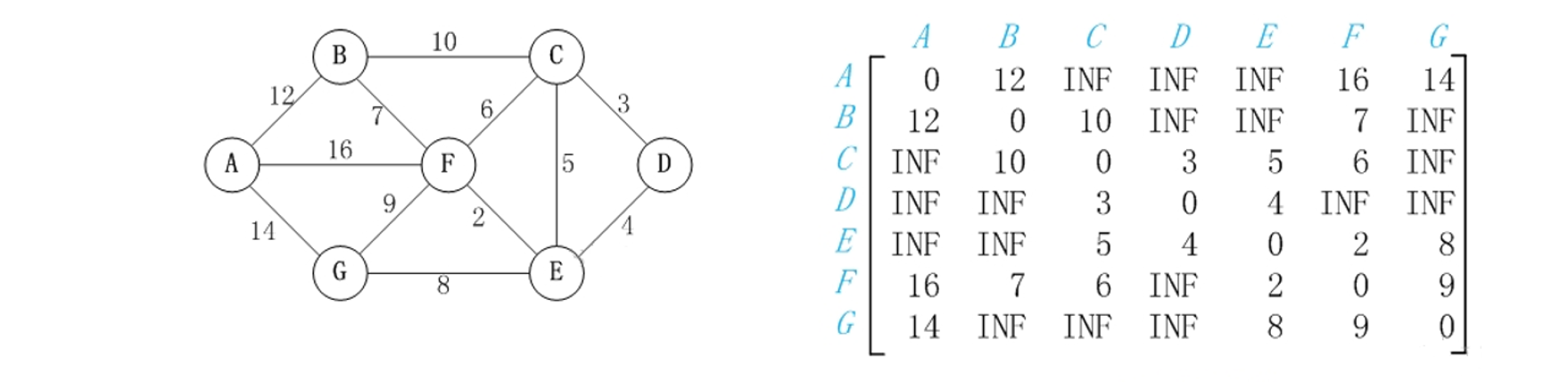
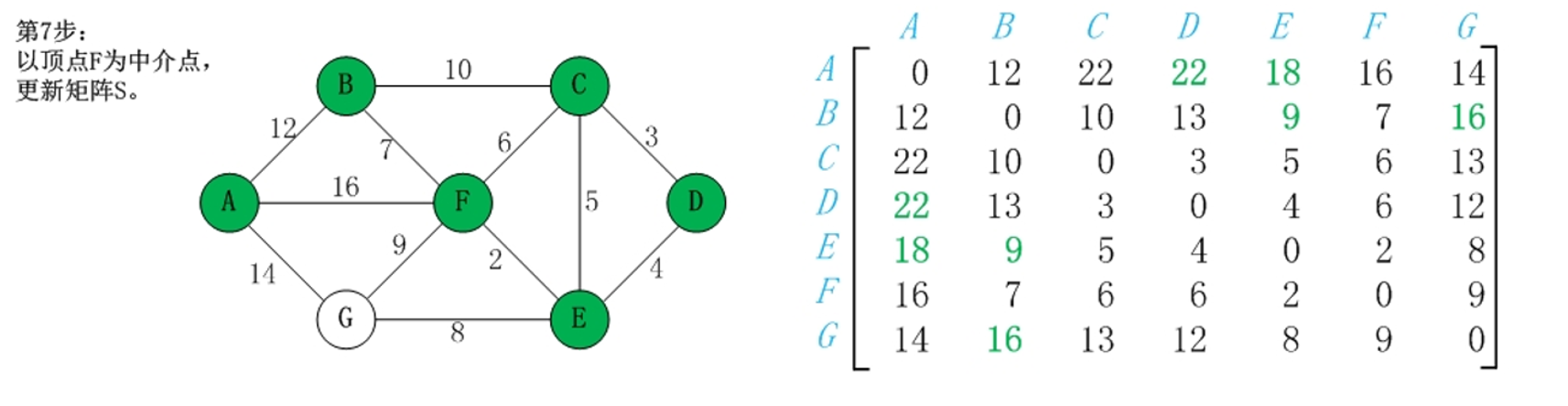
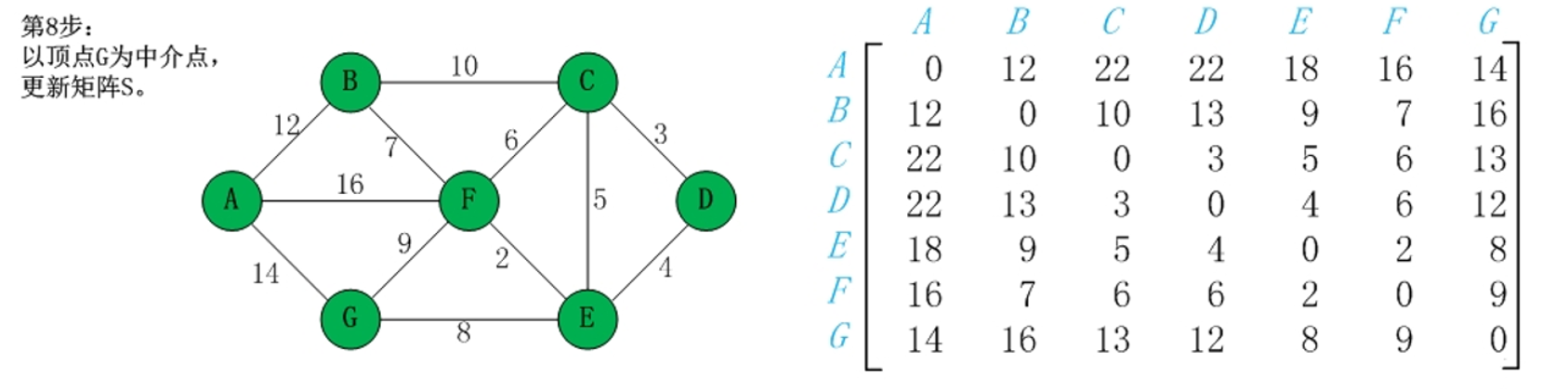
算法图解

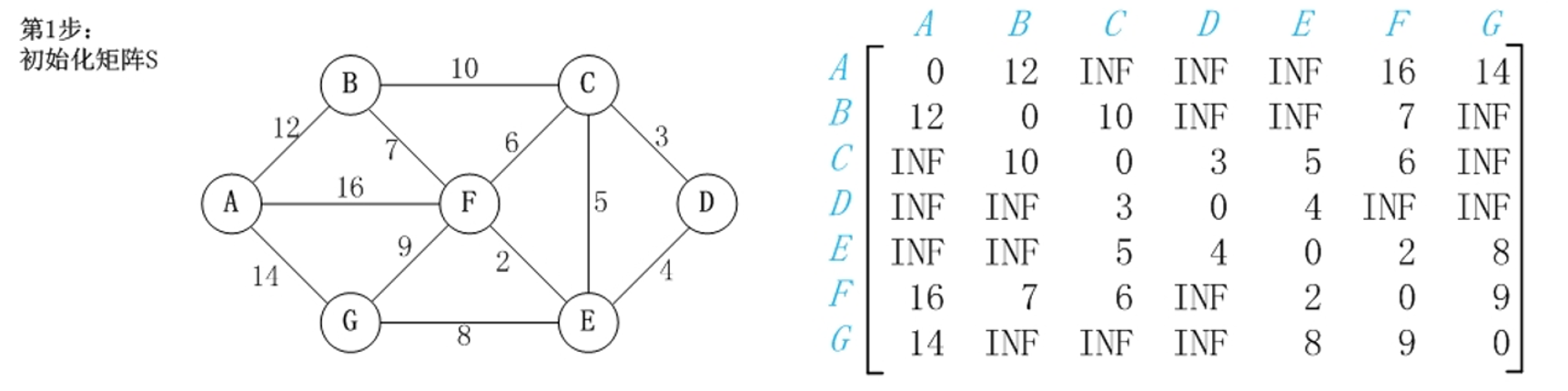
建立邻接矩阵