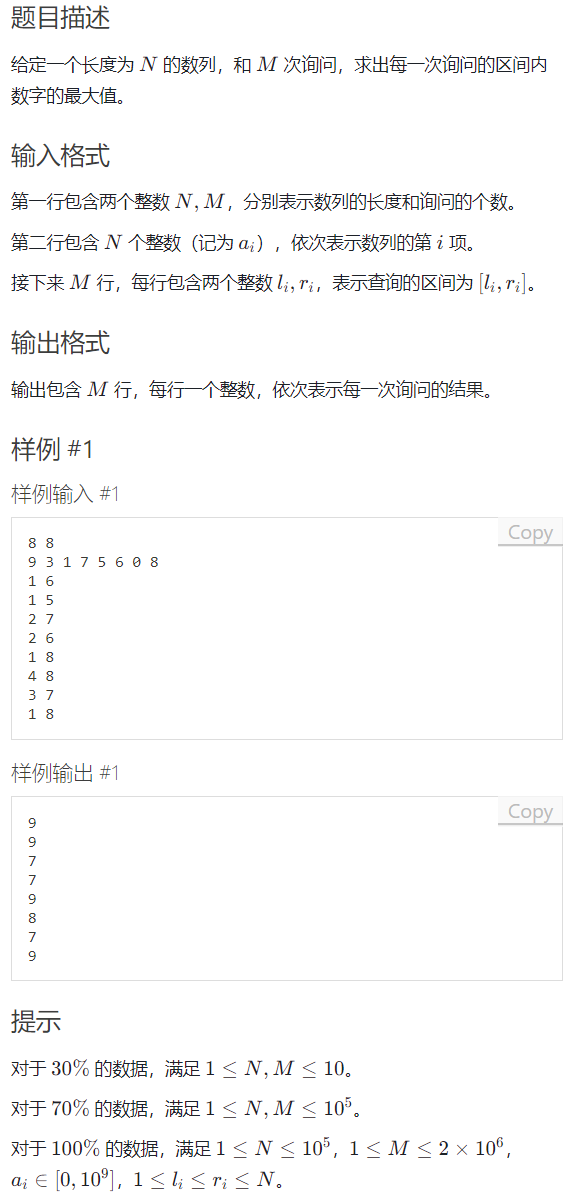
RMQ问题

RMQ（Range Minimum/Maximum Query）问题指的是：对于长度为 n 的数列 A ，回答若干次询问 RMQ（A,i,j） (i,j≤n) ，返回数列 A 中下标在 [i,j] 里的最小(大)值，也就是说， RMQ 问题是指 求区间最值的问题。

黑猫OJ #B312. ST 表 && RMQ 问题【模板】

1.朴素法暴力枚举：每次查询的时间复杂度在：O(n)，查询的次数是 m 次，即算法总时间复杂度：O(nm)，显然会超时。

参考程序

#include <bits/stdc++.h>
using namespace std;

const int N =1e5 +  10;

int n, m;
int a[N];

int main() {

    cin >> n >> m;

    for(int i = 1; i <= n; i++) cin >> a[i];

    while(m--){
        int L, R;
        cin >> L >> R;

        int maxx = -2e9;
        for(int i = L; i <= R; i++){
            if(a[i] > maxx)
                maxx = a[i];
        }
        cout << maxx << endl;
    }

    return 0;
}

2.ST 表：Sparse Table (稀疏表)，主要用来解决 RMQ 问题。应用倍增思想，可实现 O(logN) 预处理，O(1) 查询。

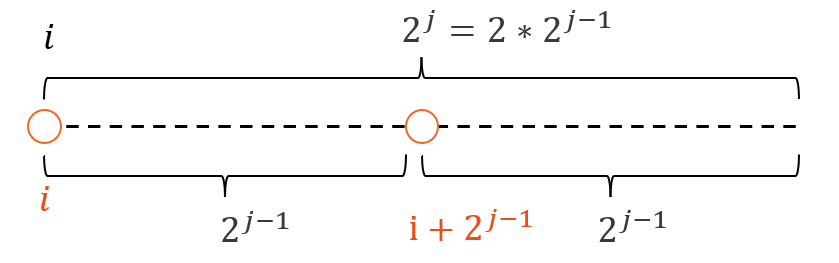
倍增法递推：用两个等长小区间拼凑一个大区间。$f[i][j]$ 以第 i 个数为起点，长度为 $2^j$ 的区间中的最大值。$(0\leq j \leq \lfloor logN \rfloor)$

$f[i][j]= max(f[i][j-1],f[i+2^{j-1} ][j-1]) (i+2^j-1 \leq n)$

• 整个区间的最大值一定是左右两个部分中最大值的较大值
• 状态转移方程：f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
• 边界条件：f[i][0] = a[i];

例如：n = 6，区间长度倍增：1，2，4，8…

$f[i][0] :[1, 1][2, 2][3, 3][4, 4][5, 5][6, 6]$

$f[i][1] :[1, 2][2, 3][3, 4][4, 5][5, 6]$

$f[i][2] :[1, 4][2, 5][3, 6]$

$j=3 : i+2^j-1=1+8 -1>6$

预处理

void init(){
    for(int j = 0; j < M; j++)
        for(int i = 1; i + (1 << j) - 1 <= n; i++)
            if(!j) f[i][j] = a[i];
            else f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}

RMQ查询

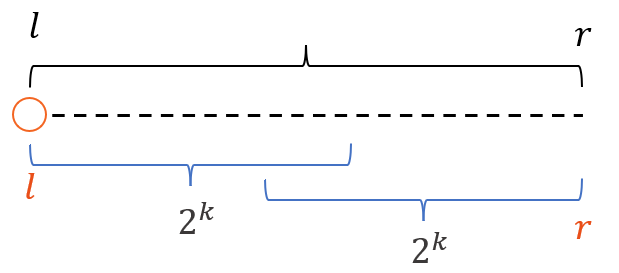
对查询区间 $[l, r]$ 做分割、拼凑，区间长度的指数 $k=log(r-l+1)$，k=0 : {1}； k=1 : {2, 3}； k=2 : {4, 5, 6,7}，观察发现： $2^k \leq r-l+1<2 \times 2^k$，即区间 $[l,r]$ 必可以用两个长度为 $2^k$ 的区间重叠拼凑。

[1,4]→[1,4]+[1,4]

[1,5]→[1,4]+[2,5]

[1,6]→[1,4]+[3,6]

[1,7]→[1,4]+[4,7]

int query(int L, int R){
    int len = R - L + 1;
    int k = log(len) / log(2);
    return max(f[L][k], f[R - (1 << k) + 1][k]);
}

$f[i][j]= max(f[i][j-1],f[i+2^{j-1}][j-1])$

预处理：O(nlogn)

查询: O(1)

空间：O(nlogn)

参考程序

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10, M = 30;

int n, m;
int a[N];
int f[N][M];

void init(){
    for(int j = 0; j < M; j++){
        for(int i = 1; i + (1 << j) - 1 <= n; i++){
            if(!j) f[i][j] = a[i];
            else f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
        }
    }
}

int query(int L, int R){
    int len = R - L + 1;
    int k = log(len) / log(2);
    return max(f[L][k], f[R - (1 << k) + 1][k]);
}

int main() {

    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d", a + i);

    init();

    while(m--){
        int L, R;
        scanf("%d%d", &L, &R);

        printf("%d\n", query(L, R));
    }

    return 0;
}