为什么需要树状数组？

当我们需要维护一个数组的前缀和S[i]=A[1]+A[2]+……+A[i]时，如果修改了任意一个A[i]，S[i]都会发生变化。在最坏情况下，会需要O(n)时间，引入树状数组后，修改和求和都是O(logn)，极大提高效率。

基本思想：根据任意正整数关于2的不重复次幂唯一分解性质，若一个正整数21的二进制表示为10101 = 242^4 + 222^2 + 202^0，因此，区间[1,x]可以分成O(logx)个小区间：

  • 长度为242^4的小区间[1, 242^4]，即[1,16]；
  • 长度为222^2的小区间[242^4 + 1, 242^4 + 222^2]，即[17,20]；
  • 长度为202^0的小区间[242^4+ 222^2 + 1, 242^4+ 222^2 + 202^0]，即[21,21]。

这些子区间共同特点是：若区间结尾为R，则区间长度就是R的二进制分解下最小的1所在位置2的次幂，设为lowbit(R)。

例如：

  • 16=10000，区间长度16=242^4；
  • 20=10100，区间长度4=222^2;
  • 21=10101，区间长度1=202^0。

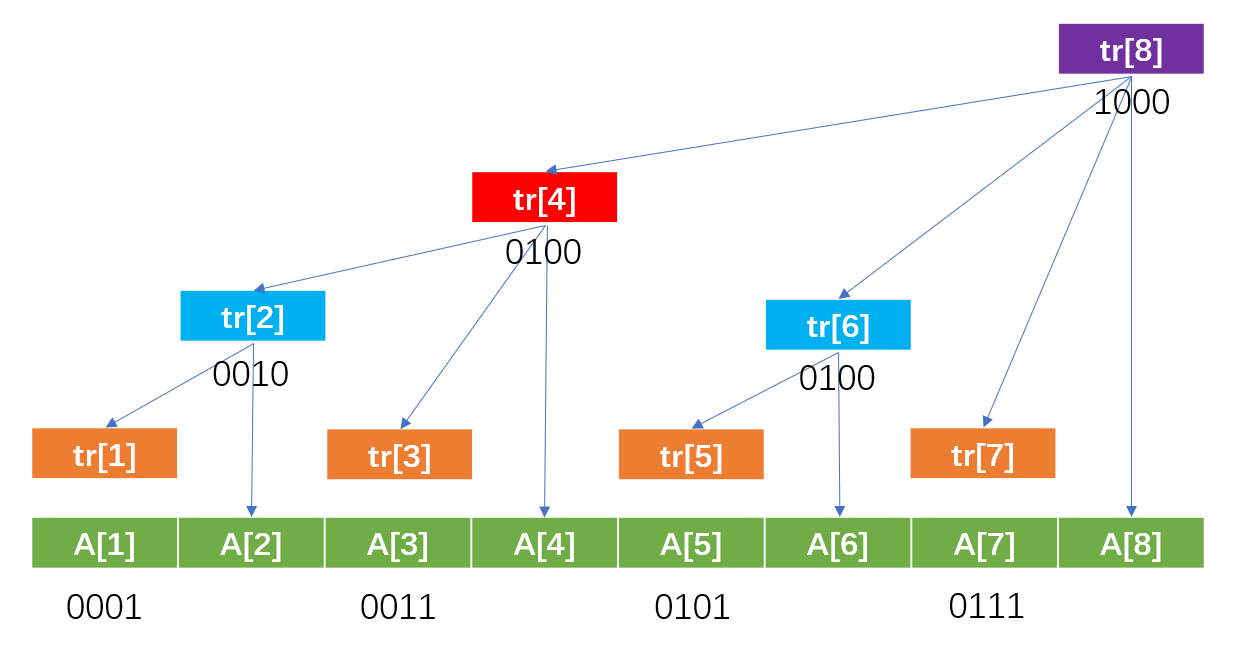
  • 1=(0001) tr[1]=A[1]
  • 2=(0010) tr[2]=A[1]+A[2]
  • 3=(0011) tr[3]=A[3]
  • 4=(0100) tr[4]=A[1]+A[2]+A[3]+A[4]
  • 5=(0101) tr[5]=A[5]
  • 6=(0110) tr[6]=A[5]+A[6]
  • 7=(0111) tr[7]=A[7]
  • 8=(1000) tr[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]

tr[i]=A[i-2k2^k+1]+A[i-2k2^k​+2]+……+A[i]

如何快速求出 i 的区间长度呢？这里我们要学习一个函数：lowbit(x) 

int lowbit(int x) { return x & (-x); }

例如，x = 20，则 -x = -20，由于计算机中负数都是以补码的形式来存储，则有如下计算过程：

(20)10=(10100)2(20)_{10}=(10100)_2

(−20)10=(01100)2(-20)_{10}=(01100)_2

单点更新

例如：当前更改A[1]，在A[1]基础之上加t

  • 1=(0001) tr[1]+=t 1+lowbit(1)=2(0010)

  • 2=(0010) tr[2]+=t 2+lowbit(2)=4(0100)

  • 4=(0100) tr[4]+=t 4+lowbit(4)=8(1000)

  • 8=(1000) tr[8]+= t 8+lowbit(8)=16(10000) 由于给定数组

    长度是8，而16超过8，因此不需要继续计算。

void update(int x, int t){
    while(x <= n){
        tr[x] += t;
        x += lowbit(x);
    }
}

查询前缀和

假定x=7，sum[7]= A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]

  • tr[7]=A[7]
  • tr[6]=A[5]+A[6]
  • tr[4]=A[1]+A[2]+A[3]+A[4]
int sum(int x){
    int res = 0;
    while(x){
        res += tr[x];
        x -= lowbit(x);
    }
    return res;
}

编程实战

黑猫OJ B215. 树状数组模板-单点修改区间查询

参考程序

#include <iostream>  
using namespace std; 

const int N = 1e6 + 10;

int n, q;
int tr[N];

int lowbit(int x){
    return x & -x;
}

void update(int x, int t){
    while(x <= n){
        tr[x] += t;
        x += lowbit(x);
    }
}

int sum(int x){
    int res = 0;
    while(x){
        res += tr[x];
        x -= lowbit(x);
    }
    return res;
}

int main(){

    cin >> n >> q;
    for(int i = 1; i <= n; i++) {
        int t;
        cin >> t;
        update(i, t);
    }

    while(q--){
        int flag;
        cin >> flag;
        if(flag){
            int i, x;
            cin >> i >> x;
            update(i, x);
        }
        else{
            int L, R;
            cin >> L >> R;
            cout << sum(R) - sum(L - 1) << endl;
        }
    }

    return 0;
}

黑猫OJ #B214. 树状数组模板-区间修改单点查询

题目分析

利用差分思想。

参考程序

#include <iostream>
#include <cstdio>
#define lowbit(x) x&-x
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;

int n, m;
LL tr[N];

void update(int x, int t){
    while(x <= n){
        tr[x] += t;
          x += lowbit(x);
    }
}

LL sum(int x){
    LL res = 0;

      while(x){
        res += tr[x];
          x -= lowbit(x);
    }

      return res;
}

int main() {

      scanf("%d%d", &n, &m);

      for(int i = 1; i <= n; i++){
        int d;
          scanf("%d", &d);
          update(i, d), update(i + 1, -d);
    }

      while(m--){
        char op[2];
          int L, R, d, x;
          scanf("%s", op);
          if(*op == 'C'){
            scanf("%d%d%d", &L, &R, &d);
              update(L, d), update(R + 1, -d);
        }
          else{
            scanf("%d", &x);
              printf("%lld\n", sum(x));
        }
    }

    return 0;
}

黑猫OJ #HM057. 区间修改区间查询

题目解析

a[1,x] 的前缀和：∑i=1xai=a1+a2+\sum_{i=1}^{x}a_i=a_1+a_2+ ... +ax+a_x

而每个 aia_i 都是我们维护的差分数组的前缀和：∑j=1idj=d1+d2+\sum_{j=1}^{i}d_j=d_1+d_2+ ... +did_i

即 a[1,x] 的前缀和：∑i=1xai=∑i=1x∑j=1idj\sum_{i=1}^xa_i=\sum_{i=1}^x\sum_{j=1}^id_j

进一步展开：

i=1→d1i=1\rightarrow d_1

i=2→d1+d2i=2\rightarrow d_1+d_2

i=3→d1+d2+d3i=3\rightarrow d_1+d_2+d_3

...

i=x→d1+d2+d3+i=x\rightarrow d_1+d_2+d_3+ ... +dx+d_x

∑i=1x=(d1+d2+d3+\sum_{i=1}^x=(d_1+d_2+d_3+... +dx)×(x+1)−(d1+2d2++d_x)\times(x+1)-(d_1+2d_2+ ... +xdx)=(x+1)∑i=1xdi−∑i=1xi×di+xd_x)=(x+1)\sum_{i=1}^xd_i-\sum_{i=1}^x i \times d_i

参考程序

#include <iostream>
using namespace std;
typedef long long LL;
const int N = 100010;

int n, m;
int a[N];
LL d1[N]; // 维护 d[i] 的前缀和
LL d2[N]; // 维护 i*d[i] 的前缀和

int lowbit(int x) { return x & -x; }

void update(LL tr[], int x, LL k) {
    while (x <= n)
    {
        tr[x] += k;
        x += lowbit(x);
    }
}

LL sum(LL tr[], int x) {
    LL res = 0;
    while (x)
    {
        res += tr[x];
        x -= lowbit(x);
    }
    return res;
}

LL prefix_sum(int x) {
    return sum(d1, x) * (x + 1) - sum(d2, x);
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++){
        scanf("%d", &a[i]);
        update(d1, i, a[i]); update(d1, i + 1, -a[i]);
        update(d2, i, (LL)a[i] * i); update(d2, i + 1, - (LL)a[i] * (i + 1));
    }

    while (m--) {
        int op, x, y, k;
        scanf("%d%d%d", &op, &x, &y);
        if (op == 1){
            scanf("%d", &k);
            // 区间修改
            update(d1, x, k), update(d2, x, x * k);
            update(d1, y + 1, -k), update(d2, y + 1, - (y + 1) * k);
        }      
        else
            printf("%lld\n", prefix_sum(y) - prefix_sum(x - 1));
    }
    return 0;
}

黑猫OJ #B217. 校门外的树【进阶】

题目分析

在一个区间 [i, j] 上种树，我们可以在 i 处放一个左括号，在 j 处放一个右括号，表示区间 [i, j] 种了树。

可以发现，查询某个区间树的种类个数时，如区间 [i, j]，只要拿 j（ 包括j ）之前的左括号数量 减去 i（ 不包括 i）之前的右括号数量即可。

故用两个树状数组分别维护左右括号的前缀和，更新时记录左右括号数，查询时相减即能得到结果。

参考程序

#include <iostream>  
using namespace std; 

const int N = 5e4 + 10;

int n, m;
int trl[N], trr[N];

int lowbit(int x){
    return x & -x;
}

void update(int x, int t, int tr[]){
    while(x <= n){
        tr[x] += t;
        x += lowbit(x);
    }
}

int sum(int x, int tr[]){
    int res = 0;
    while(x){
        res += tr[x];
        x -= lowbit(x);
    }
    return res;
}

int main(){

    cin >> n >> m;

    while(m--){
        int op, L, R;
        cin >> op >> L >> R;
        if(op == 1)
            update(L, 1, trl), update(R, 1, trr);
        else
            cout << sum(R, trl) - sum(L - 1, trr) << endl;
    }

    return 0;
}

results matching ""

    No results matching ""