什么是树形结构？

在现实生活中有很多体现树的逻辑的例子，比如企业里的职级关系，就是一个树。

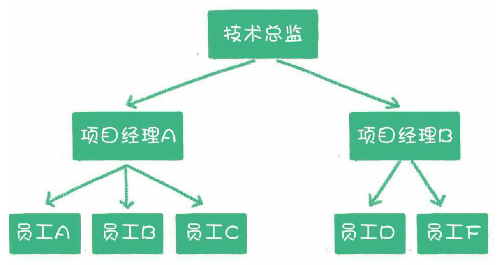
树的定义

树（Tree）是n（n≥0）个结点的有限集。

n=0 时称为空树。

在任意一棵非空树中：

（1）有且仅有一个特定的结点称为根（root）的结点。

（2）当 n>1 时，除根结点外，其余结点可分为 m（m>0）个互不相交的有限集 $T_1,T_2,....,T_m$ , 其中每一个集合本身又是一棵树，并且称为根的子树（SubTree）。

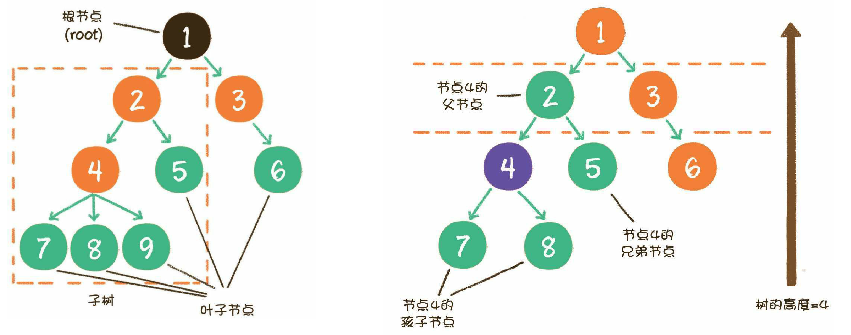
对于树的定义还需要注意两点：

1.n>0 时，根结点是唯一的，不可能存在多个根结点。

2.m>0 时，子树的个数没有限制，但它们一定是互不相交的。如图中的两个结构就不符合树的定义，因为它们都有相交的子树。

树的相关概念

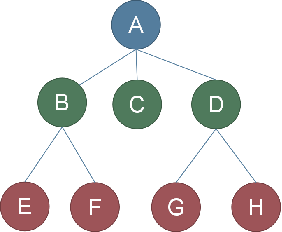
根结点

例：A

**度指的是一个结点的子结点的数量，一棵树的度是指树中最大的结点度**

例：结点 B 的度为 2，结点 D 的度为 3，树的度为 3。

分支结点：度不为 0 的结点

例：A B D F

叶子结点：度为 0 的结点

例：E J G H I C

孩子：一个结点子树的根

例：G H I 是 D 的孩子

双亲：如果 B 是 A 的孩子，那么 A 是 B 的双亲

例：D 是 G H I 的双亲

兄弟：同一双亲的孩子间互称兄弟

例：G H I 互为兄弟

祖先：从根到某个结点所经过的分支上的所有结点称为该结点的祖先

例：J 的祖先有：A B F

子孙：某结点子树中所有结点都是该结点的子孙例：B 的子孙有 E F J

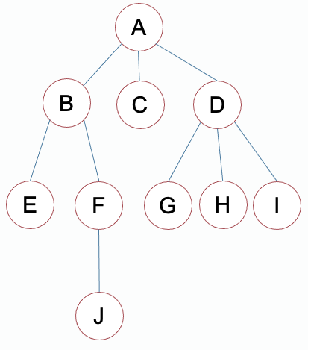
找树根和孩子

题目描述

给定一棵树，输出树的根root，孩子最多的结点max以及他的孩子。

输入

第一行：n（结点个数≤100），m（边数≤200）。

以下m行：每行两个结点x和y，表示y是x的孩子(x,y≤1000)。

输出

第一行：树根：root；

第二行：孩子最多的结点max；

第三行：max的孩子（按编号由小到输出）。

样例

4
2 
6 7 8

提示

如果存在多个最大,取编号小的那个。

题目解析：

1.tr[y] = x 表示 y 的双亲结点为 x。

2.由于结点编号未必连续，因此每出现一个结点都需要标记。

3.mp[x] 记录 x 的子结点数量。

参考程序：

#include <iostream>
#include <map>
using namespace std;

const int N = 110;

int n, m;
int tr[N];
bool book[N];
map<int, int> mp;

int main() {

    cin >> n >> m;
    while(m--){
        int x, y;
        cin >> x >> y;
        tr[y] = x;
        mp[x]++;
        book[x] = true;
        book[y] = true;
    }

    for(int i = 1;  i < N; i++){
        if(tr[i] == 0 && book[i]){
            cout << i << endl;
            break;
        }
    }   

    int cnt = -1, p = -1;
    for(auto x: mp){
        if(x.second > cnt){
            cnt = x.second;
            p = x.first;
        }
    }

    cout << p << endl;

    for(int i = 1; i < N; i++)
        if(tr[i] == p)
            cout << i << " ";

    return 0;
}

单词查找树

题目描述

在进行文法分析的时候，通常需要检测一个单词是否在我们的单词列表里。为了提高查找和定位的速度，通常都画出与单词列表所对应的单词查找树，其特点如下：

1．根结点不包含字母，除根结点外每一个结点都仅包含一个大写英文字母；

2．从根结点到某一结点，路径上经过的字母依次连起来所构成的字母序列，称为该结点对应的单词。单词列表中的每个单词，都是该单词查找树某个结点所对应的单词；

3．在满足上述条件下，该单词查找树的结点数最少。

4．如图所示左边的单词列表就对应于右边的单词查找树。注意，对一个确定的单词列表，请统计对应的单词查找树的结点数（包含根结点）。

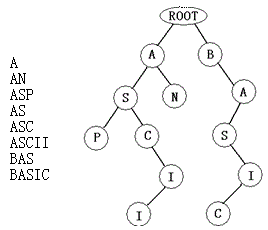
输入格式

为一个单词列表，每一行仅包含一个单词和一个换行/回车符。每个单词仅由大写的英文字母组成，长度不超过63个字母。文件总长度不超过32K，至少有一行数据。

输出格式

仅包含一个整数，该整数为单词列表对应的单词查找树的结点数。

样例

A
AN
ASP
AS
ASC
ASCII
BAS
BASIC

题目解析

首先要对建树的过程有一个了解。对于当前被处理的单词和当前树：在根结点的子结点中找单词的第一位字母，如果存在则进而在该结点的子结点中寻找第二位字母……

如此下去直至单词结束，那么就不需要在该树中添加结点；或单词的第 n 位不能被找到，即将单词的第 n 位及其后的字母依次加入单词查找树中去。

**但，本问题只是问你结点总数，而非建树方案，且有 32K 文件，可以考虑能不能不通过建树就直接算出结点数？**

问题本质：一个单词相对于另一个单词的差：设单词 2 的长度为 L，且与单词 1 从第 N 位开始不一致，则说单词 2 相对于单词 1 的差为 L-N

可见，将一个单词加入单词树的时候，需加入的结点数等于该单词与单词树中单词之差的最小值。

单词的字典顺序排列后的序列则具有类似的特性，即在一个字典顺序序列中，第 m 个单词相对于第 m-1 个单词的差必定是它对于前 m-1 个单词的差中最小的。于是，得出建树的等效算法：

① 读入数据；

② 对单词列表进行字典顺序排序；

③ 依次计算每个单词对前一单词的差，并把差累加起来。注意：第一个单词相对于【空】的差为该单词的长度；

④ 累加和再加上1（根结点），输出结果。

就给定的样例，按照这个算法求结点数的过程如下表：

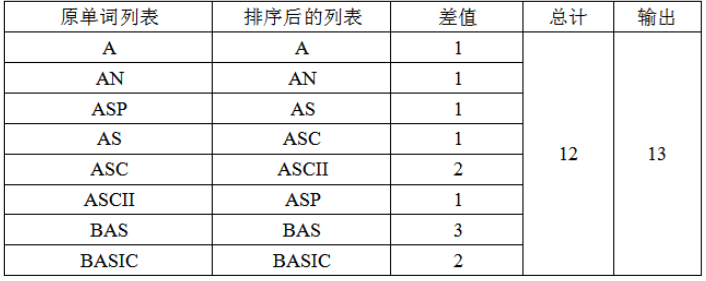
数据结构：

先确定 32K（32*1024=32768 字节）的文件最多有多少单词和字母。当然应该尽可能地存放较短的单词。

因为单词不重复，所以长度为 1 的单词（单个字母）最多 26 个；

长度为2的单词最多为 26*26=676 个；因为每个单词后都要一个换行符（换行符在计算机中占 2 个字节），所以总共已经占用的空间为：(1+2)*26+(2+2)*676=2782 字节；

剩余字节（32768-2782=29986 字节）分配给长度为 3 的单词（长度为 3 的单词最多有 26*26*26=17576 个）有 29986/(3+2）≈ 5997。

所以单词数量最多为 26+676+5997=6699。

定义一个数组：string words[7000]；把所有单词连续存放起来，用选 sort 进行排序。

参考程序

#include <iostream>
#include <string>
#include <algorithm>
using namespace std;

string words[7000];
int n = 1;

int main() {

    while(cin >> words[n++]);
    n--;

    sort(words + 1, words + n + 1);

    int res = words[1].size();

    for(int i = 2; i <= n; i++){
        int j = 0;
        while(j < words[i - 1].size()){
            if(words[i][j] != words[i - 1][j])
                break;
            j++;
        }
        res += words[i].size() - j;
    }

    cout << res + 1 << endl;

    return 0;
}

什么是二叉树？

二叉树（Binary Tree）是树的一种特殊形式。二叉，顾名思义，这种树的每个结点最多有 2 个孩子结点。注意，这里是最多有 2 个，也可能只有 1 个，或者没有孩子结点。

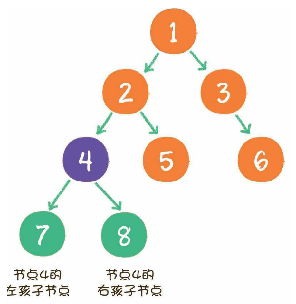
满二叉树

**一个二叉树的所有非叶子结点都存在左右孩子，并且所有叶子结点都在同一层级上，那么这个树就是满二叉树。**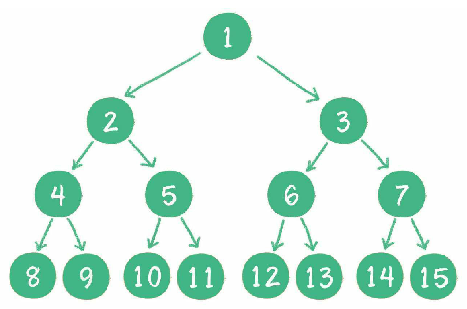

完全二叉树

对于深度为 k 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应时称之为完全二叉树。

**前 k-1 层是满的，最后一层不满，但是最后一层从左到右是连续的。**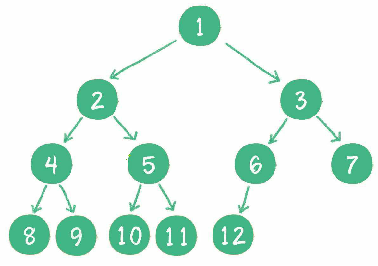

二叉树的五条性质

性质1

在二叉树的第 i 层上最多有 $2^{i-1}$ 个结点。（i≥1）

第 1 层是根结点，只有 1 个，所以 $2^{1-1}$ = $2^0$ =1。

第 2 层有 2 个， $2^{2-1}$ = $2^1$ =2。

第 3 层有 4 个， $2^{3-1}$ = $2^2$ =4。

第 4 层有 8 个， $2^{4-1}$ = $2^3$ =8。

通过数学归纳法的论证该结论。

性质2

二叉树中如果深度为 k，那么最多有 $2^k$ -1个结点。(k≥1）注意这里一定要看清楚，是 $2^k$ 后再减去 1，而不是 $2^{k-1}$ 。切记不可与性质 1 混淆！

如果有 1 层，至多 1= $2^1$ -1 个结点。

如果有 2 层，至多 1+2=3= $2^2-1$ 个结点。

如果有 3 层，至多 1+2+4=7= $2^3$ -1 个结点。

如果有 4 层，至多 1+2+4+8=15= $2^4$ -1 个结点。

通过数学归纳法的论证该结论。

性质3

对任意一棵二叉树，如果其叶结点数为 $n_0$ ，度为 2 的结点数为 $n_2$ ，则一定满足： $n_0=n_2+1$ 。

因为二叉树中所有结点的度数均不大于 2，所以结点总数（记为n）应等于 0 度结点数 $n_0$ 、1 度结点 $n_1$ 和 2 度结点数 $n_2$ 之和：

$n=n_0+n_1+n_2$ ……(式子1)

分支总线数=n-1= $n_1+2n_2$ ……(式子2)

由式子 1 和式子 2 得到： $n_0=n_2+1$

性质4

具有 n 个结点的完全二叉树的深度为 ⌊ $log_2n$ ⌋+1。

假设深度为 k，则根据完全二叉树的定义，前面 k-1 层一定是满的，所以 n> $2^{k-1}$ -1。但 n 又要满足 n≤ $2^k$ -1。

所以， $2^{k-1}$ –1<n≤ $2^k$ -1。变换一下为 $2^{k-1}$ ≤n< $2^k$ 。

以 2 为底取对数得到：k-1≤ $log_2n$ <k。而 k 是整数，所以 k= ⌊ $log_2n$ ⌋ +1 。

性质5

根结点位置为 1，对于第 x 位置的结点

左孩子：第 2x 位置

右孩子：第 2x+1 位置

双亲：第 $\frac{x}{2}$ 位置

二叉树存储结构

二叉树数组存储

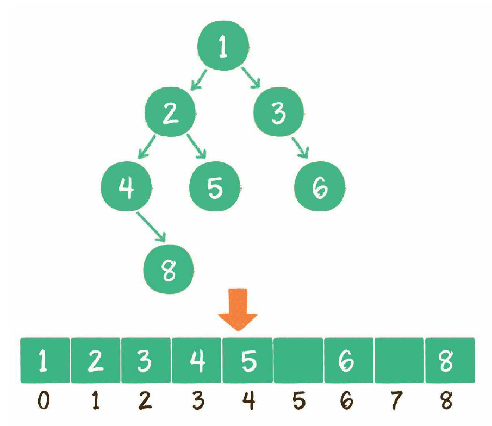
**如果对应位置没有结点，那么在存储时需要预留出这个位置。为了读取数据时可以还原出二叉树结构。**

二叉树链式存储

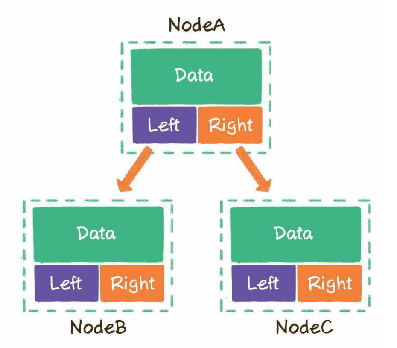
二叉树遍历

前序遍历

规则是若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树（根->左子树->右子树）。

中序遍历

规则是若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树（左子树->根->右子树）。

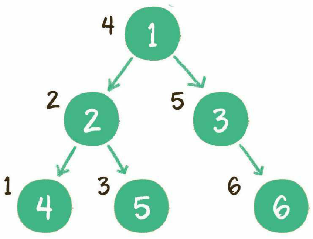
后序遍历

规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点（左子树->右子树->根）。

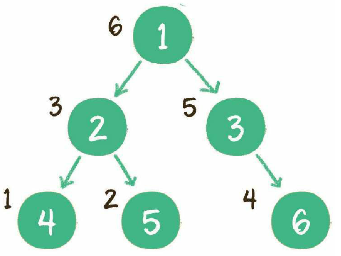
层序遍历

借助队列实现层次遍历

访问根结点，根结点入队；
结点出队，访问该结点的孩子结点，并将该结点的孩子结点入队；
重复步骤2，直至队列为空。

随堂练习-选择题

例题1

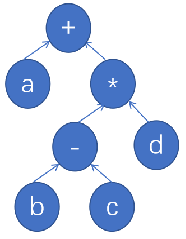
对表达式 a+(b-c)*d 的前缀表达式为（），其中 +、-、* 是运算符。

A. *+a-bcd

B. +a*-bcd

C. abc-d*+

D. abc-+d

答案：B

解析：按照运算优先级建立如下表达式树，然后进行前序遍历。

例题2

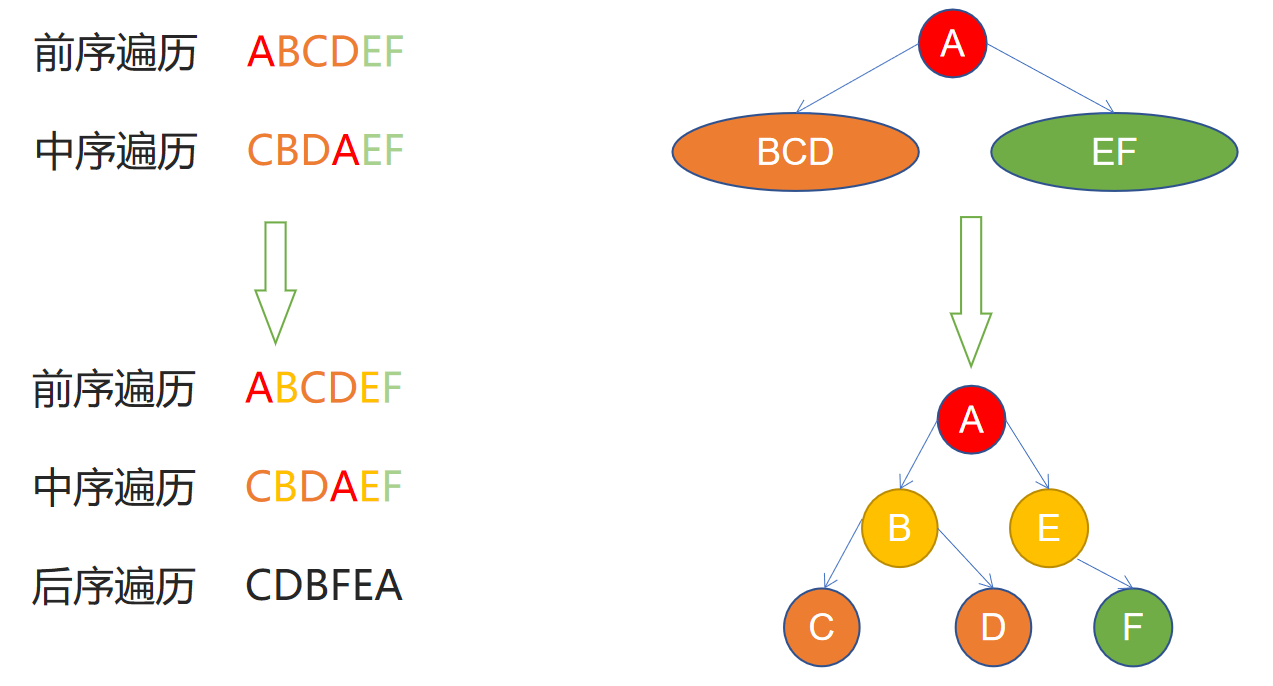
**给定先序遍历和中序遍历，求后序遍历。**

先序遍历 ABCDEF

中序遍历 CBDAEF

解析：

首先在前序中找到根：A；

再中序中用根分出左右两部分：CBD 和 EF；

再先序中找到这两部分的根 B 和 E；

一直如此往复即可。

二叉树形态和树的计数问题

二叉树五种基本形态：

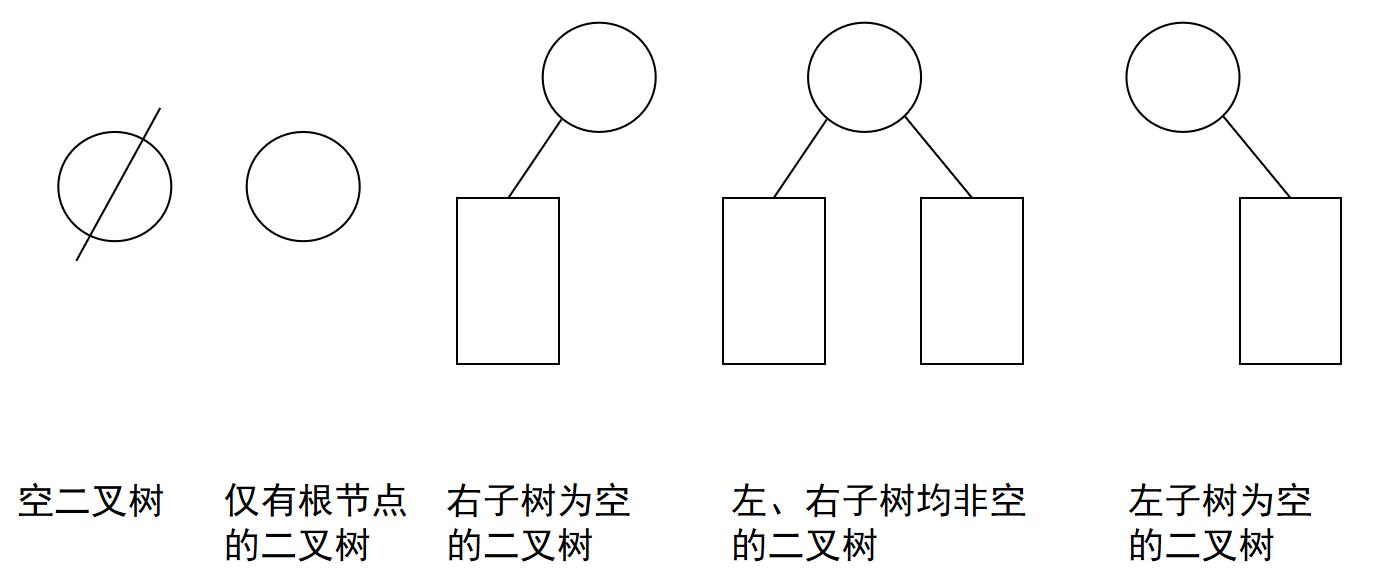
3 个结点二叉树五种形态：

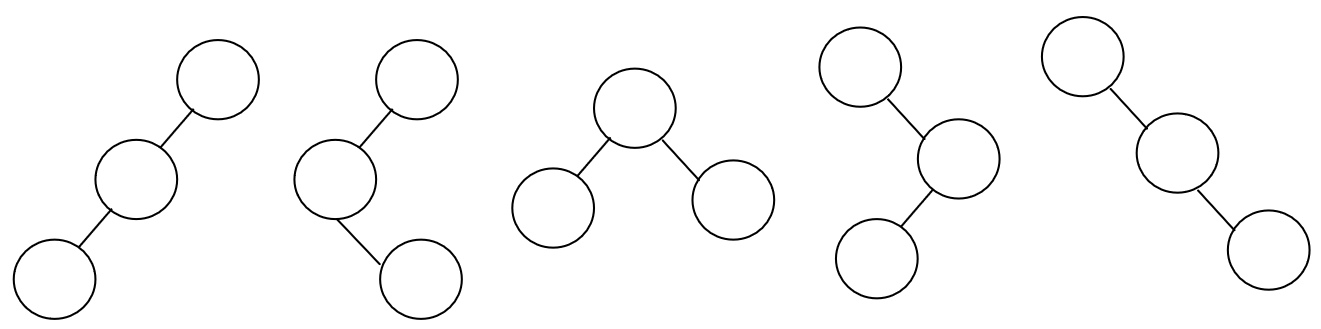
那么 n 个结点的不同形态二叉树有多少棵？

一般情况下，一棵具有 n（n>1）个结点的二叉树可以看做是一个根节点、一颗具有 i 个结点的左子树和一颗具有 n-i-1 个结点的右子树组成，其中 0≤0≤n-1。

A[0]=1

A[1]=1

A[n]= $\sum_{i=0}^{n-1}A[i]*A[n-i-1]$

这是 Catalan 数的形式之一，等价于 $C_{2n}^n*\frac{1}{n+1}$

二叉树先序、中序求后序

题目描述

输入一棵二叉树的先序和中序遍历序列，输出其后序遍历序列。

输入

共两行，第一行一个字符串，表示树的先序遍历，第二行一个字符串，表示树的中序遍历。树的结点一律用小写字母表示。

输出

一行，表示树的后序遍历序列。

样例

abdec
dbeac

debca

题目解析

1.通过先序遍历找到根节点；

2.在中序遍历中找到根节点位置，并划分左、右子树，且可以得到左、右子树长度；

3.在先序遍历序列中根据左、右子树长度找到对应左、右子树序列；

4.分别对得到的左、右子树继续做先序遍历划分，直至子树为空返回。

参考程序

#include <iostream>
#include <string>
using namespace std;

void postOrder(string pre_string, string in_string){
    int len = pre_string.size();
    if(!len) return;

    char root = pre_string[0];
    int in_root_idx = in_string.find(root);

    string pre_left_tree = pre_string.substr(1, in_root_idx);
    string in_left_tree = in_string.substr(0, in_root_idx);

    postOrder(pre_left_tree, in_left_tree);

    string pre_right_tree = pre_string.substr(in_root_idx + 1);
    string in_right_tree = in_string.substr(in_root_idx + 1);

    postOrder(pre_right_tree, in_right_tree);

    cout << root;
}

int main() {

    string pre_string, in_string;
    cin >> pre_string >> in_string;

    postOrder(pre_string, in_string);

    return 0;
}

扩展二叉树

题目描述

由于先序、中序和后序序列中的任一个都不能唯一确定一棵二叉树，所以对二叉树做如下处理，将二叉树的空结点用·补齐，如图所示。我们把这样处理后的二叉树称为原二叉树的扩展二叉树，扩展二叉树的先序和后序序列能唯一确定其二叉树。

现给出扩展二叉树的先序序列，要求输出其中序和后序序列。

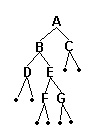
输入

扩展二叉树的先序序列。

输出

输出其中序和后序序列。

样例

ABD..EF..G..C..

DBFEGAC
DFGEBCA

题目解析

1.建树：每次读取一个字符，如果不是.，存储到数据域，然后递归创建左、右子树，返回该结点编号；

2.中序、后续遍历二叉树。

参考程序

#include <iostream>
using namespace std;

const int N = 110;

struct BNode{
    char ch;
    int lchild, rchild;
}node[N];

int root = 0, cnt = 0;

int build_tree(int T){

    char ch;
    cin >> ch;
    if(ch == '.') return 0;

    T = ++cnt;
    node[T].ch = ch;
    node[T].lchild = build_tree(T);
    node[T].rchild = build_tree(T);

    return T;
}

void in_order(int T){
    if(!T) return;

    in_order(node[T].lchild);
    cout << node[T].ch;
    in_order(node[T].rchild);
}

void post_order(int T){
    if(!T) return;
    post_order(node[T].lchild);
    post_order(node[T].rchild);
    cout << node[T].ch;
}

int main() {

    root = build_tree(0);
    in_order(root);
    cout << endl;
    post_order(root);

    return 0;
}

12-树和二叉树

什么是树形结构？

树的定义

树的相关概念

找树根和孩子

单词查找树

什么是二叉树？

满二叉树

完全二叉树

二叉树的五条性质

性质1

性质2

性质3

性质4

性质5

二叉树存储结构

二叉树数组存储

二叉树链式存储

二叉树遍历

前序遍历

中序遍历

后序遍历

层序遍历

随堂练习-选择题

例题1

例题2

二叉树形态和树的计数问题

二叉树先序、中序求后序

扩展二叉树

results matching ""

No results matching ""