数据结构概念
数据结构有三个要素:
逻辑结构
物理结构
数据的运算
逻辑结构是指数据元素之间的逻辑关系。
更贴近于现实,即从逻辑关系上来描述数据。
是独立于计算机的,与计算机内部如何存储是无关的。
线性结构:线性表,栈,队列,双队列,串
非线性结构:集合、高维数组,树形结构、图状结构
物理结构:是指数据结构在计算机内的表示,也称为存储结构。

线性表与链表
线性表:是n个具有相同特性的数据元素的有限序列。
线性表中数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其它数据元素都有且只有一个前趋元素,有且只有一个后继元素。
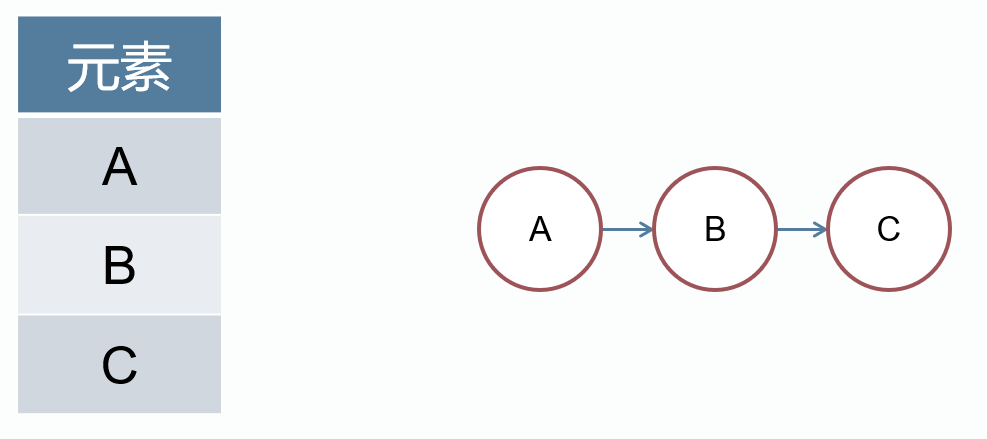
顺序存储结构的线性表,也叫顺序表。
链式存储结构的线性表,也叫链表。
链表有头结点。

链表
单链表
链表结点
struct Node{
DataType val; //DataType:数据类型 val: 数据的值
int next; //下一个结点的地址
};
内存管理
Node node[N]; //内存池,MAXN:最大结点数量
int p = 1; //内存指针,指向等待被分配的结点

分配结点
int np = p++;
node[np]即为被分配的节点
头结点
头结点:该结点无数据,其next指向链表的第一个结点
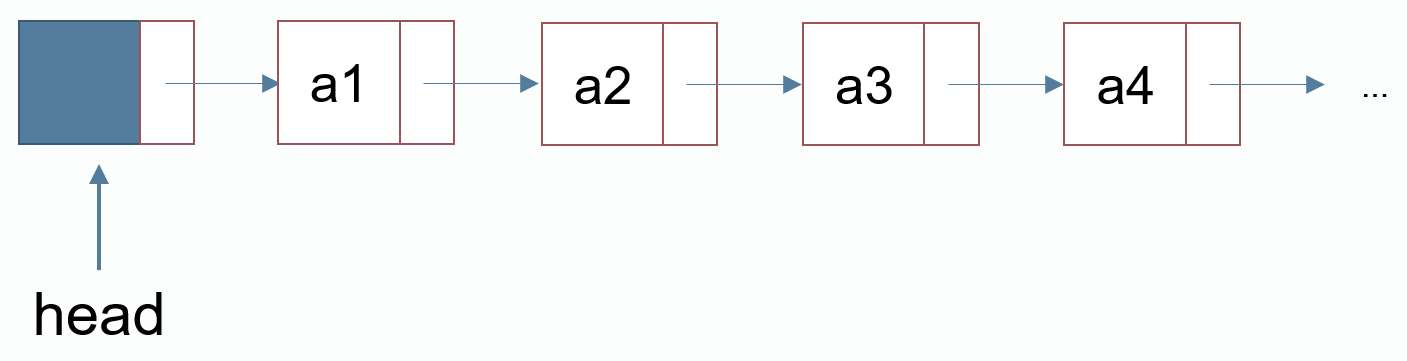
int head = p++; //申请一个结点,该结点地址为head
node[head] 使用头结点
尾指针
尾指针:指向链表的最后一个结点
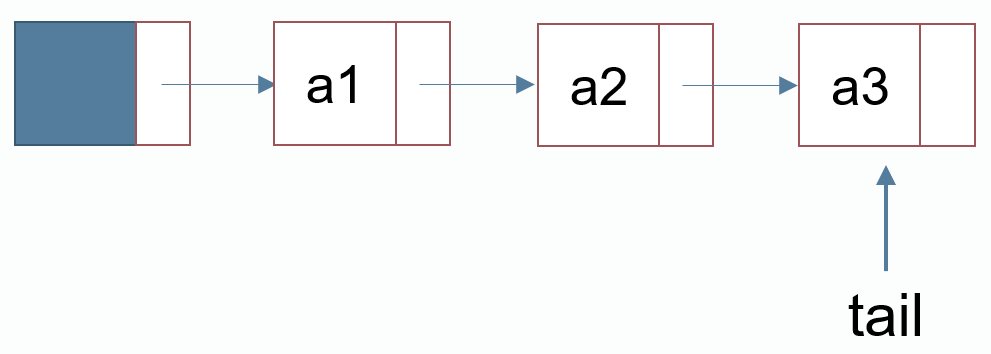
int tail = head; //初始情况下尾指针指向头结点
结点地址
结点地址(结点指针):结点在node数组中的下标
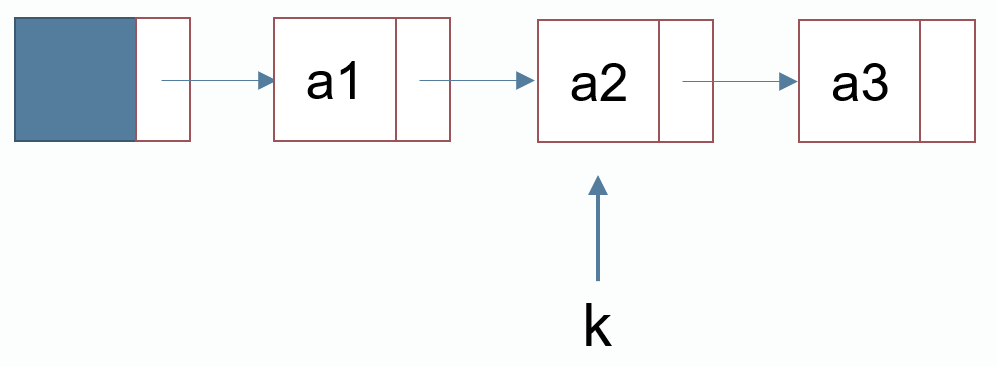
取结点地址k指向的结点:node[k]
尾插法添加结点
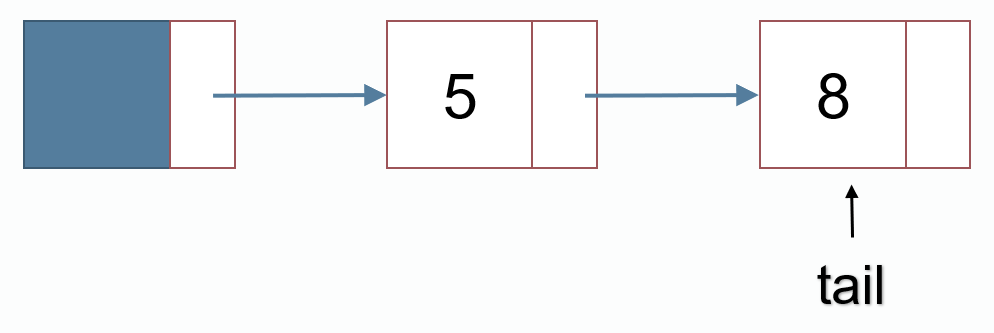
int np = p++; //申请一个结点 地址为np
node[np].val = 8;
node[tail].next = np;
tail = np;
头插法添加结点
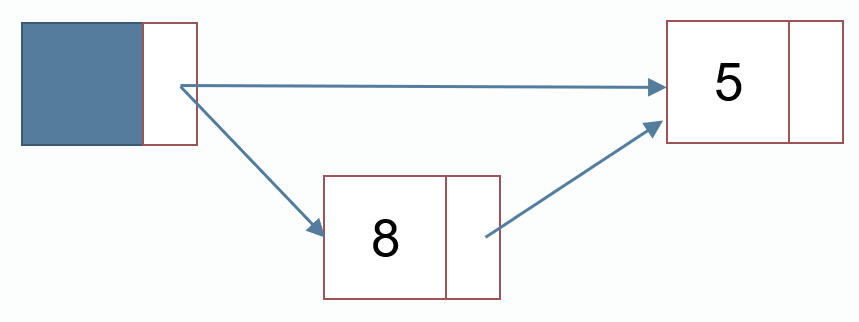
int np = p++;
node[np].val = 8;
node[np].next = node[head].next;
node[head].next = np;
遍历链表
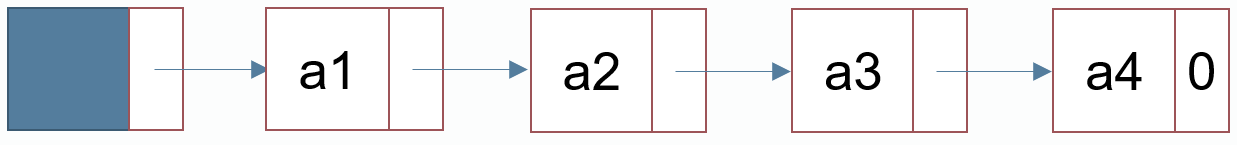
for(int i = node[head].next; i != 0; i = node[i].next){
//...
//此时取到结点为node[i]
}
链表插入(在k指向的结点后插入)
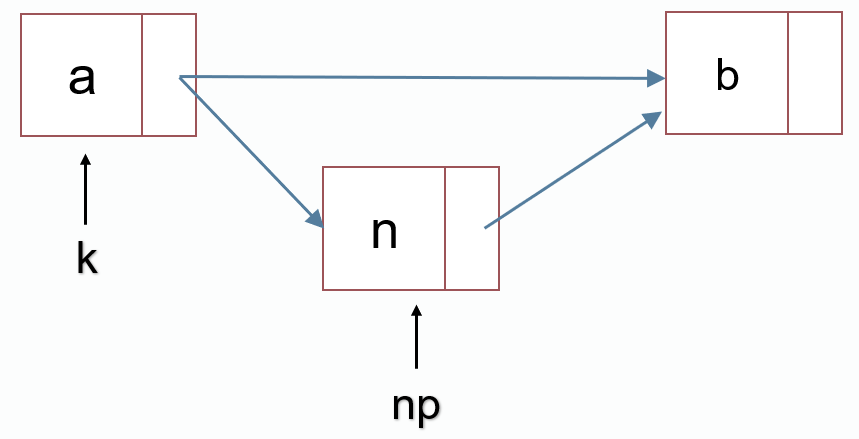
int np = p++;
node[np].next = node[k].next;
node[k].next = np;
链表删除(删除k指向的结点的下一个结点)
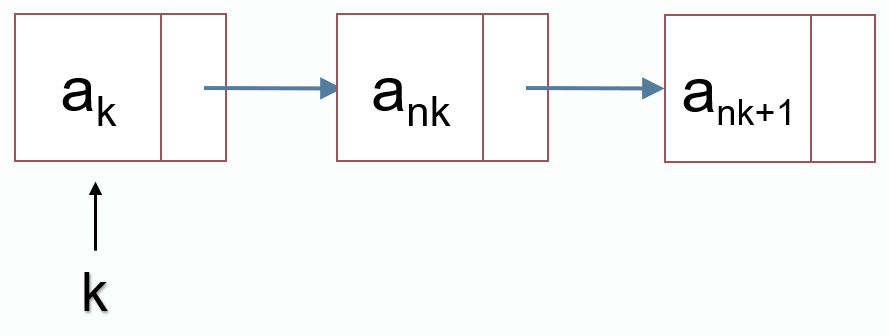
int nk = node[k].next;
node[k].next = node[nk].next;
双链表
双向静态链表
struct Node {
DataType val;//DataType:数据类型
int pre; //pre:前一个结点的地址
int next; //next:下一个结点的地址
};


尾插法添加结点
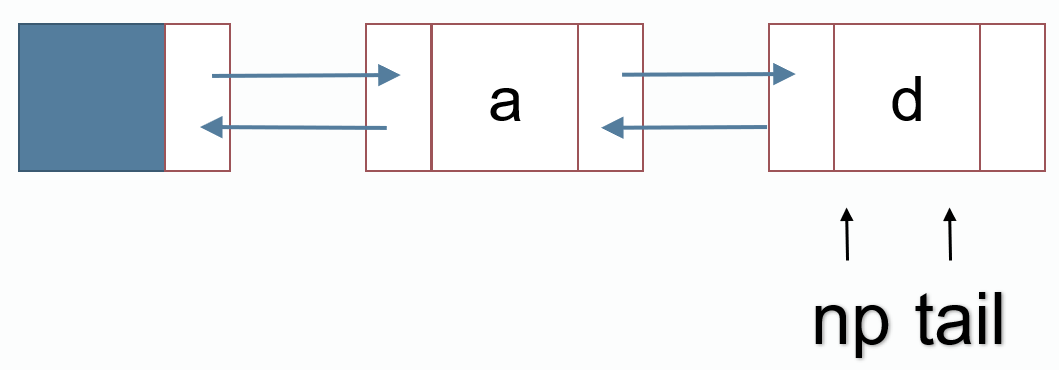
int np = p++; //申请一个结点 地址为np
node[np].val = d;
node[tail].next = np;
node[np].pre = tail;
tail = np;
链表插入(在k指向的结点前插入,返回新结点地址)

int pk = node[k].pre;
int np = p++;
node[np].val = d;
node[np].next = k;
node[np].pre = pk;
node[k].pre = np;
node[pk].next = np;
头插法添加结点
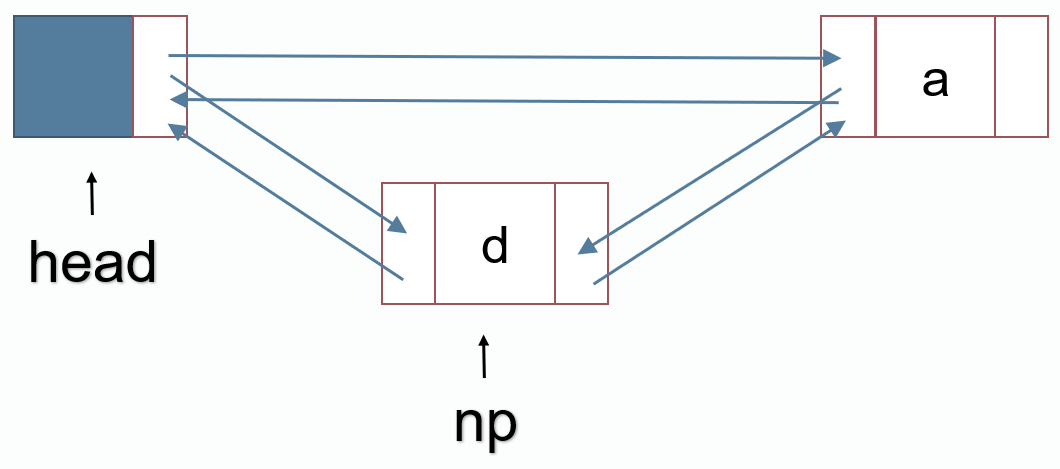
int np = p++;
node[np].val = d;
node[np].next = node[head].next;
node[np].pre = head;
node[node[head].next].pre = np;
node[head].next = np;
链表删除(删除k指向的结点)
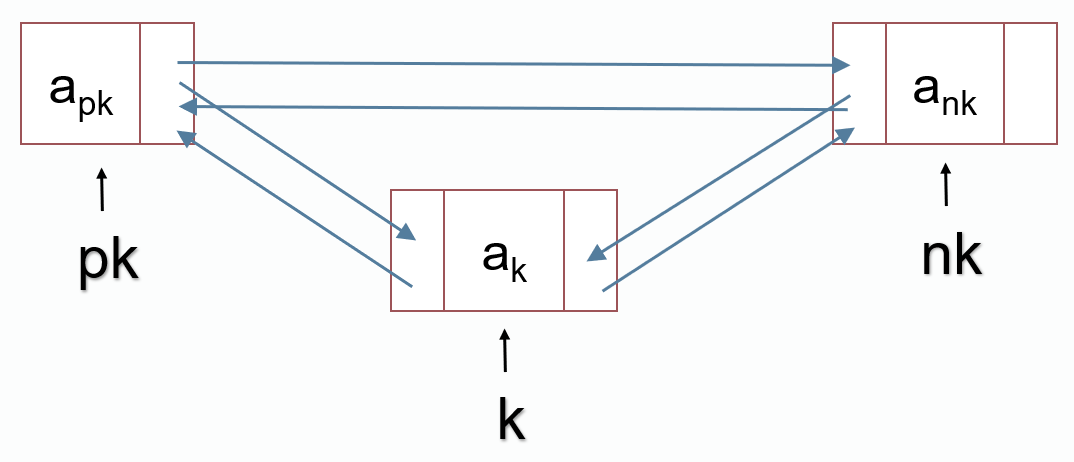
int pk = node[k].pre;
int nk = node[k].next;
node[pk].next = nk;
node[nk].pre = pk;
线性表的两种存储结构顺序表与链表

C++ STL 双向链表

使用迭代器遍历list
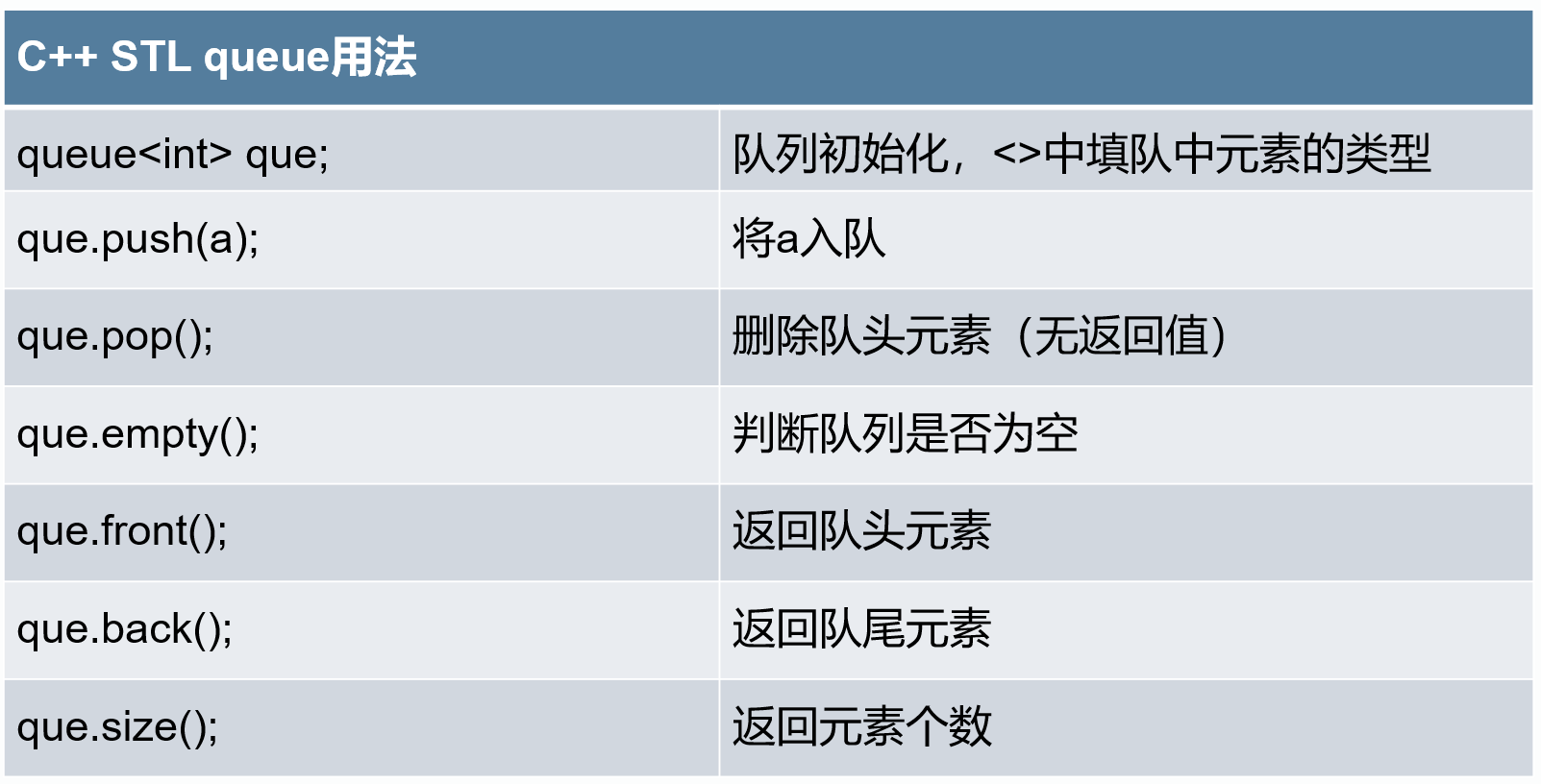
list<int> lst;
//添加数据代码
for(list<int>::iterator it = lst.begin(); it != lst.end(); ++it) {
cout << *it << endl;
}
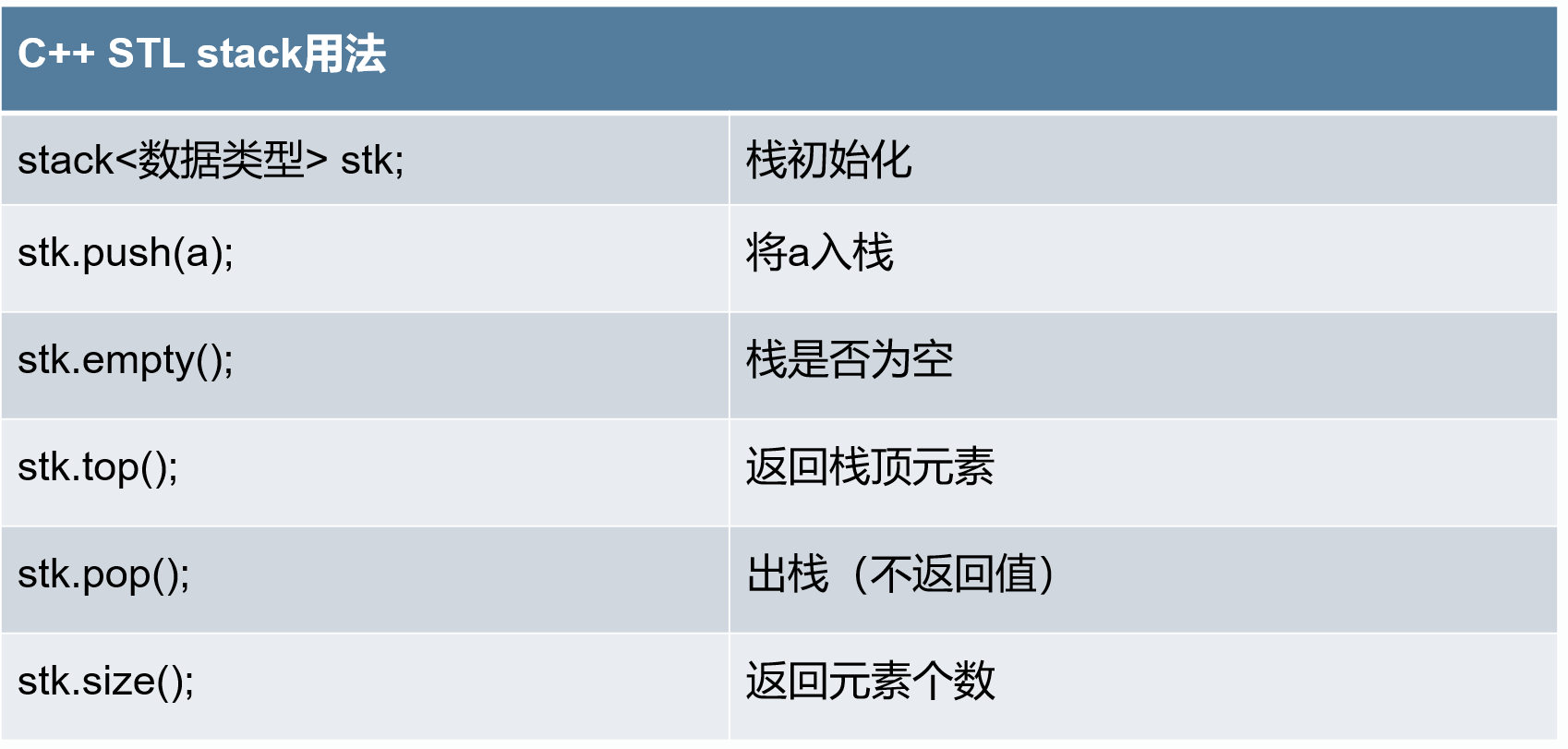
栈
要理解是栈,我们需要先举一个生活中的例子。
假如有一个又细又长的圆筒,圆筒一端封闭,另一端开口。往圆筒里放入乒乓球,先放入的靠近圆筒底部,后放入的靠近圆筒入口。

那么,要想取出这些乒乓球,则只能按照和放入顺序相反的顺序来取,先取出后放入的,再取出先放入的,而不可能把最里面最先放入的乒乓球优先取出。

栈(stack)是一种线性数据结构,它就像一个上图所示的放入乒乓球的圆筒容器,栈中的元素只能先入后出(First In Last out,简称FILO),最后进入的元素存放的位置叫作栈顶。

入栈操作(push)就是把新元素放入栈中,只允许从栈顶一侧放入元素,新元素的位置将会成为新的栈顶。
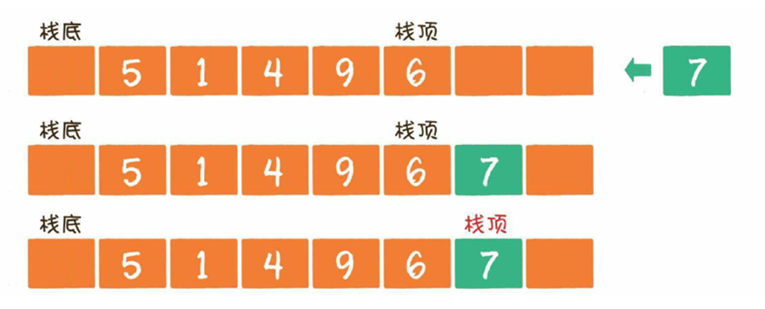
出栈操作( pop )就是把元素从栈中弹出,只有栈顶元素才允许出栈,出栈元素的前一个元素将会成为新的栈顶。
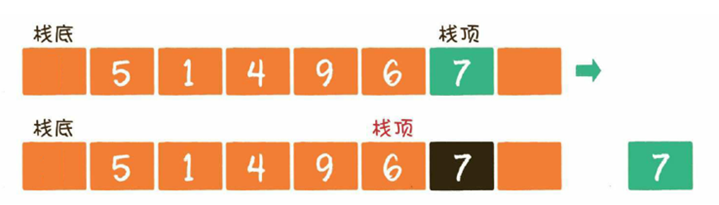
接下来,我们使用数组模拟栈,栈底指针不指向具体元素。
栈的逻辑结构
栈(stack):是一种受限定的线性表,限定其插入和删除操作只能在表的一端进行。
栈顶:允许操作的一端
栈底:不允许操作的一端
入栈 / 压栈 / 进栈(push):添加数据
出栈 / 弹栈 / 退栈(pop):删除数据
栈的特点:后进先出
表达式求值问题
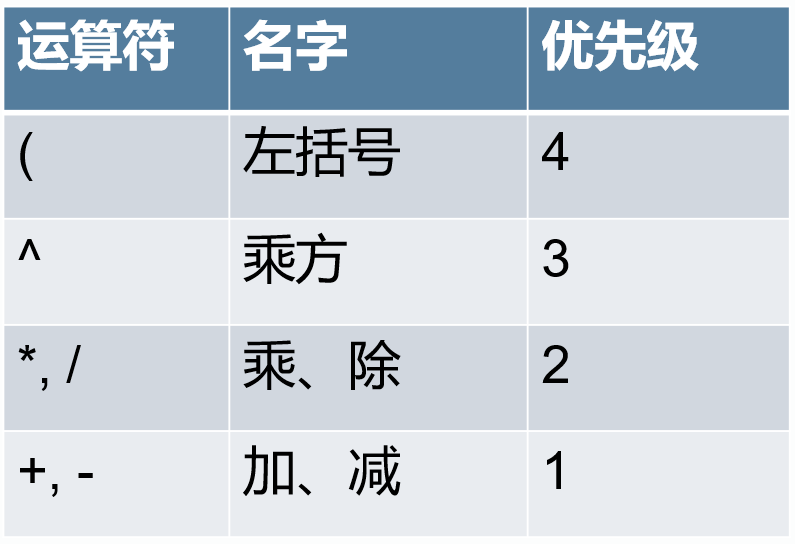
中缀表达式:运算符位于操作数之间。
例:(3+4)×5-6
前缀表达式(波兰表达式):运算符位于操作数之前。
例:-×+3456
后缀表达式(逆波兰表达式):运算符位于操作数之后。
例:34+5×6-
例:求后缀表达式 34+5×6-的 值
求解后缀表达式
从左向右扫描字符串
遇到数字时,将数字入栈。
遇到运算符时,弹出栈顶的两个数,用该运算符对它们做相应的计算,结果入栈。
扫描结束后,栈顶数字就是结果。

带括号的中缀表达式转后缀
如果其他运算符在准备入栈时栈顶是左括号,运算符直接入栈。
如果右括号在准备入栈时,遇到栈顶是左括号,那么左括号出栈,这次入栈结束。
中缀:(1+2) * (6-5)
后缀:1 2 + 6 5 - *
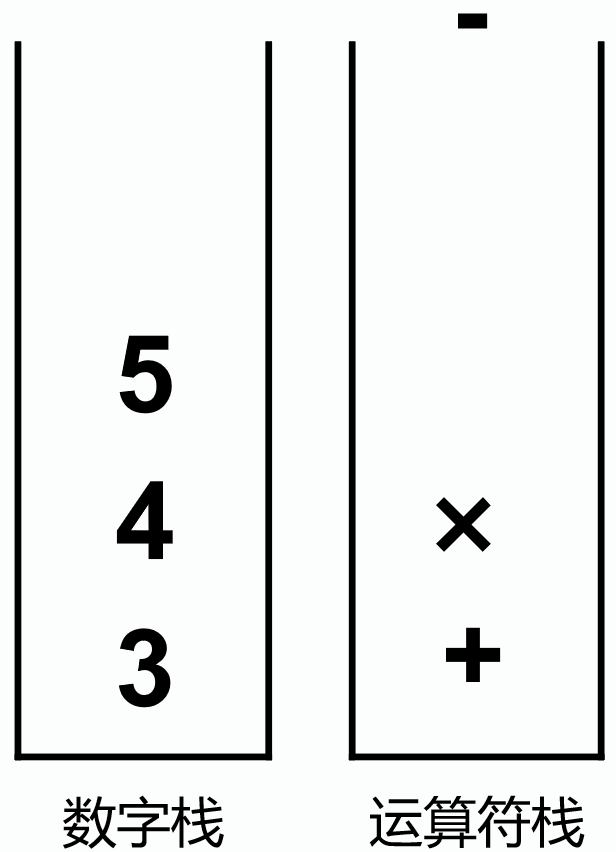
例:求3+4×5-6的值
从左向右扫描表达式
遇到数字进数字栈
遇到运算符,如果运算符栈栈空,或该运算符优先级大于栈顶运算符优先级,则入栈。否则运算符出栈,从数字栈出栈2个数字,进行计算,结果在数字栈入栈。重复此过程。
扫描结束后,运算符栈出栈运算符,进行运算,直到运算符栈为空。最后数字栈栈顶的数字,就是结果。
队列
要理解什么是队列,我们同样可以用一个生活中的例子来说明。
假如公路上有一条单行隧道,所有通过隧道的车辆只允许通过隧道入口驶入,从隧道出口驶出,不允许逆行。这就是队列结构。


队列是限定在一端进行插入,另一端进行删除特殊线性表。就像排队买东西,排在前面的人买完东西后离开队伍(删除),而后来的人总是排在队伍未尾(插入)。通常把队列的删除和插入分别称为出队和入队。允许出队的一端称为队头,允许入队的一端称为队尾。所有需要进队的数据项,只能从队尾进入,队列中的数据项只能从队头离开。由于总是先入队的元素先出队(先排队的人先买完东西),这种表也称为先进先出(FIFO)表。
队列的数组实现

队列的链表实现

入队( enqueue )就是把新元素放入队列中,只允许在队尾的位置放入元素,新元素的下一个位置将会成为新的队尾。
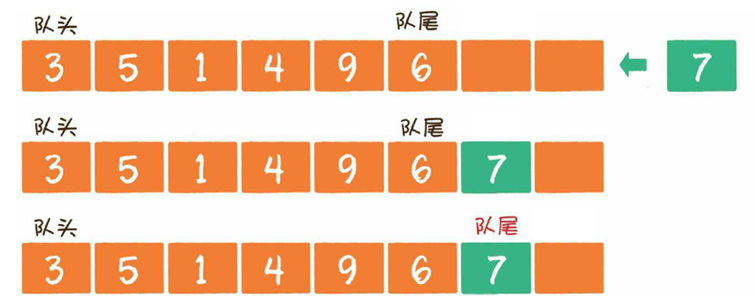
出队操作( dequeue )就是把元素移出队列,只允许在队头一侧移出元素,出队元素的后一个元素将会成为新的队头。

队列的逻辑结构
队列(queue):是一种特殊的线性表,仅允许在一端插入,而在另一端删除。
队尾(tail):允许插入数据的一端
队头(head):允许删除数据的一端
入队(enqueue):插入数据
出队(dequeue):删除数据
队列的特点:先进先出