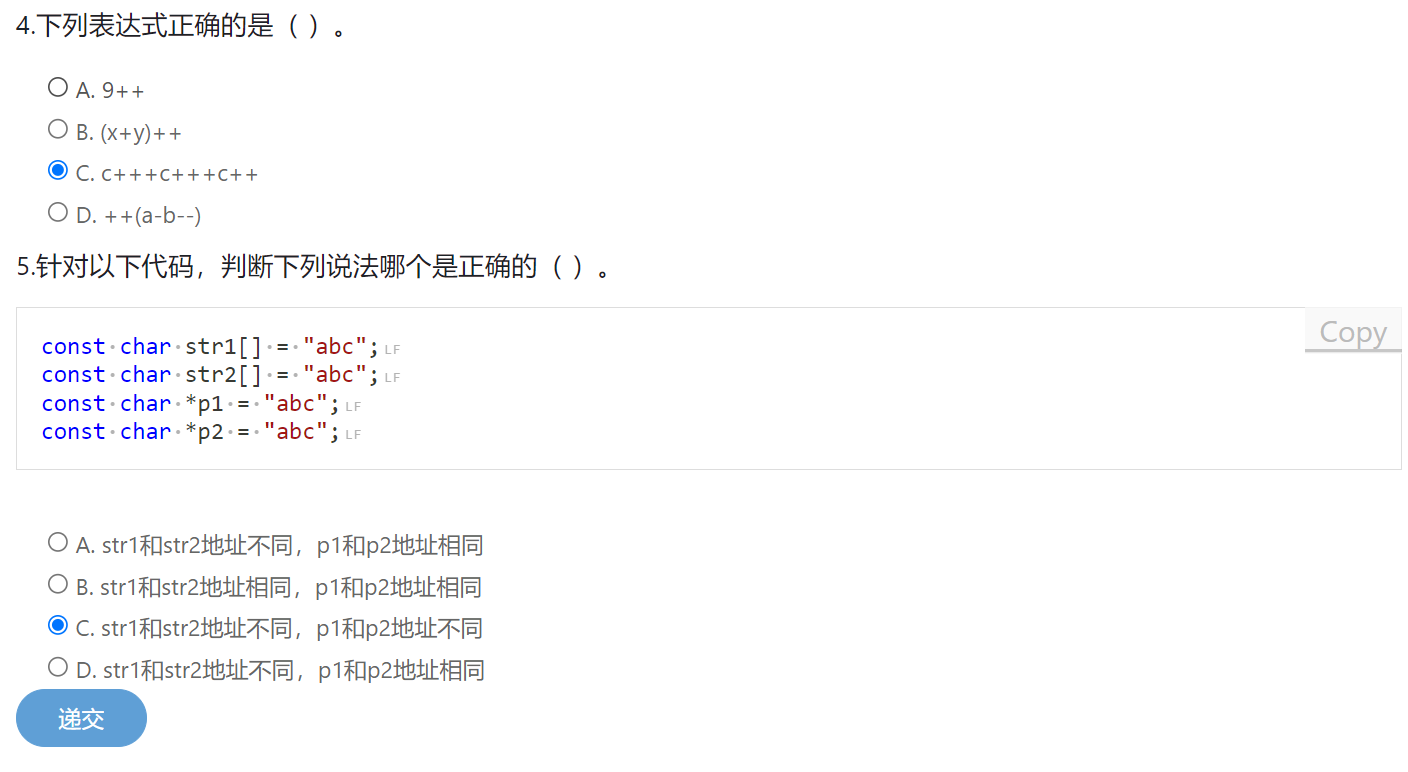
单项选择题

求阶乘的和
题目描述
求S=1!+2!+3!+....+n!。
输入格式
输入正整数n。
输出格式
输出S。
样例
3
9
提示
对于所有数据:1≤n≤20。
参考程序
#include <iostream>
using namespace std;
typedef long long LL;
int main() {
int n;
cin >> n;
LL res = 0, t = 1;
for(int i = 1; i <= n; i++){
t *= i;
// cout << t << " ";
res += t;
}
cout << res <<endl;
return 0;
}
判断偶数
题目描述
输入两个不相等的四位正整数N(1000≤N≤9999)和M(1000≤M≤9999),其中N<M,中间以一个空格隔开,输出N与M之间(包含N和M)所有满足要求的正整数且正整数之间以一个英文逗号隔开。
要求每个正整数的各个位上的数都为偶数。(注:0为偶数)
输入格式
在—行输入两个不相等的四位正整数N和M。(N和M之间以一个空格隔开)
输出格式
输出N与M之间(包含N和M)所有满足要求的正整数且正数之间以一个英文逗号隔开。
样例
4000 4008
4000,4002,4006,4008
参考程序
#include <bits/stdc++.h>
using namespace std;
bool check(int n){
while(n){
if(n % 2)
return false;
n /= 10;
}
return true;
}
int main() {
int n, m;
cin >> n >> m;
bool is_first = true;
for(int i = n; i <= m; i++){
if(check(i)){
if(is_first)
is_first = false;
else
cout << ',';
cout << i;
}
}
return 0;
}
计数问题
题目描述
输入一个正整数 n (1≤n≤1000),统计从 1 到 n 之间(包含 1 和 n)所有正整数中 0,1,2,3,4,5,6,7,8,9 的数字分别出现的次数,且按样例分行输出(按 0 到 9 顺序输出,英文逗号前为 0 到 9 的数字,逗号后为该数字出现的次数)。
例如::n 为 12,那么 1 到 n 之间所有的正整数有 1,2,3,4,5,6,7,8,9,10,11,12。
在 12 个正整数中数字 0 出现了 1 次数字 1 出现了 5 次数字 2 出现了 2 次数字 2,3,4,5,6,7,8,9 分别出现了 1 次。
输入格式
一行一个正整数 n。
输出格式
0,0出现的次数
1,1出现的次数
......
1,1出现的次数
样例
10
0,1
1,2
3,1
4,1
5,1
6,1
7,1
8,1
9,1
参考程序
#include <bits/stdc++.h>
using namespace std;
int a[10];
void f(int n){
while(n){
a[n % 10]++;
n /= 10;
}
}
int main() {
int n;
cin >> n;
for(int i = 1; i <= n; i++)
f(i);
for(int i = 0; i < 10; i++)
printf("%d,%d\n", i, a[i]);
return 0;
}
最长公共子串
题目描述
分行输入两个字符串(2≤字符串长度≤100),找出两个字符串中最大的公共子串。
然后将公共子串及公共子串的长度分行输出。
输入格式
第一行输入一个字符串;
第二行输入一个字符串。
输出格式
第一行输出最大公共子串;
第二行输出最大公共子串长度。
样例
abcdab
baabcd
abcd
4
参考程序
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int n, m;
char a[N], b[N];
int f[N][N];
string s;
void work(int n, int m){
if(n == 0 || m == 0) return;
if(a[n] == b[m]){
s += a[n];
work(n - 1, m - 1);
}
else{
if(f[n][m] == f[n - 1][m])
work(n - 1, m);
else if(f[n][m] == f[n][m - 1])
work(n, m - 1);
}
}
int main() {
scanf("%s%s", a+1,b+1);
n = strlen(a + 1);
m = strlen(b + 1);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(a[i]==b[j])
f[i][j]=max(f[i][j],f[i-1][j-1]+1);
}
}
work(n, m);
for(int i = s.size() - 1; i >= 0; i--)
cout << s[i];
printf("\n%d\n", f[n][m]);
return 0;
}
最少操作次数
题目描述
输入两个整数n(0<n<100001)和k (0<k<100001),通过对n连续进行加1或减1或乘以2这3种操作,使得n最后结果正好等于k (同一种操作可以使用多次也可以不使用),要求最后输出最少的操作次数。
例如: n为5,k为17,通过减1、乘以2、乘以2、加1四次操作得到17,也就是$5-1=4$、$42=8$、$82=16$、$16+1=17$。
输入格式
输入两个整数n和k(n和k之间以一个空格隔开)。
输出格式
输出最少的操作次数。
样例
5 17
4
参考程序
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
struct Node{
int v, step;
}q[N];
int n, k;
bool book[N];
int bfs(){
int hh = 0, tt = -1;
q[++tt] = {n, 0};
book[n] = true;
while(hh <= tt){
auto t = q[hh++];
if(t.v == k){
return t.step;
}
int x1 = t.v + 1, x2 = t.v - 1, x3 = t.v * 2;
if(x1 < N && !book[x1]){
book[x1] = true;
q[++tt] = {x1, t.step + 1};
}
if(x2 >= 0 && !book[x2]){
book[x2] = true;
q[++tt] = {x2, t.step + 1};
}
if(x3 < N && !book[t.v * 2]){
book[x3] = true;
q[++tt] = {x3, t.step + 1};
}
}
}
int main() {
cin >> n >> k;
cout << bfs();
return 0;
}
回型取数
题目描述
用户分行输入两个正整数(2≤正整数≤20),第一个数代表数字矩阵的行数,第二个数代表数字矩阵的列数,数字矩阵的数字为从1开始的正整数,根据回形取数规则将最终的数字线路输出(数字线路中的每个数字之间需要有一个英文逗号隔开)。
输入格式
第一行输入一个正整数作为行数;
第二行输入一个正整数作为列数。
输出格式
根据回形取数规则将数字线路输出(数字线路中的每数字之间需要有一个英文逗号隔开)。
样例
3
2
1,3,5,6,4,2
提示
回形取数是沿着一个数字矩阵的左上角向下开始移动取数当前方没有数字或者数字已经被取过就会逆时针转动继续移动取数当没有数可取时回形取数结束,如下图所示:
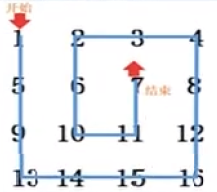
回形取数结束后会产生一条线路图,也就是数字线路。
为:1,5,9,13,14,15,16,12,8,4,3,2,6,10,11,7。
参考程序
#include <bits/stdc++.h>
using namespace std;
const int N = 25;
int n, m;
int a[N][N];
int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1}, d = 0;
int main() {
cin >> n >> m;
int t = 0;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
a[i][j] = ++t;
cout << 1;
int x = 1, y = 1;
a[1][1] = -1;
for(int i = 2; i <= n * m; i++){
int nx = x + dx[d], ny = y + dy[d];
if(nx < 1 || nx > n || ny < 1 || ny > m || a[nx][ny] == -1){
d = (d + 1) % 4;
nx = x + dx[d], ny = y + dy[d];
}
cout << ',' << a[nx][ny];
x = nx, y = ny;
}
return 0;
}
带分数
题目描述
100 可以表示为带分数的形式:100 = 3 +$\frac{69258}{714}$。
还可以表示为:100 = 82 + $\frac{3546}{197}$。
注意特征:带分数中,数字1~9分别出现且只出现一次(不包含0)。
类似这样的带分数,100 有 11 种表示法。
输入格式
一行一个正整数N (1≤N<${10}^6$)
输出格式
输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。
样例
100
11
105
6
参考程序
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10;
int n;
bool book[N], bookbak[N];
int ans = 0;
bool check(int a, int c){
LL b = n * (LL)c - a * c;
if(!a || !b || !c) return false;
memcpy(bookbak, book, sizeof book);
while(b){
int x = b % 10;
b /= 10;
if(!x || bookbak[x]) return false;
bookbak[x] = true;
}
for(int i = 1; i <= 9; i++)
if(!bookbak[i])
return false;
return true;
}
void dfs_c(int u, int a, int c){
if(u > 9) return;
if(check(a, c)) ans++;
for(int i = 1; i <= 9; i++)
if(!book[i]){
book[i] = true;
dfs_c(u + 1, a, c * 10 + i);
book[i] = false;
}
}
void dfs_a(int u, int a){
if(a >= n) return;
if(a) dfs_c(u, a, 0);
for(int i = 1; i <= 9; i++)
if(!book[i]){
book[i] = true;
dfs_a(u + 1, a * 10 + i);
book[i] = false;
}
}
int main() {
cin >> n;
dfs_a(0, 0);
cout << ans << endl;
return 0;
}